Метод отраслевых бета-коэффициентов

Исследования Р. Леви еще в 1970;х гг. показали, что для любой акции ее бета-коэффициент не является устойчивым во времени и поэтому не может служить точной оценкой будущего риска. В то же время бета-коэффициент портфеля, состоящего даже из 10 случайно выбранных акций, достаточно устойчив и, следовательно, может рассматриваться в качестве приемлемой меры риска этого портфеля.

Другой аргумент за переход к отраслевым оценкам — бета-коэффициент показывает в значительной степени отраслевую реакцию на макроэкономические подвижки (изменения в деловом цикле, инфляционные всплески и т. п.). Компании потребительских отраслей (В2С), энергетические компании имеют бетакоэффициент меньше единицы. Цикличные компании, чувствительные к деловому циклу и потребительским предпочтениям (металлургические, автомобилестроительные, производители сложной бытовой техники, девелоперы), имеют бета-коэффициент больше единицы (на уровне 1,2—1,4). Выше единицы бета-коэффициент и у компаний финансового сектора (банки, инвестиционные, страховые компании). Еще более высокие значения бета-коэффициента показывают высокотехнологичные компании, у которых высока неопределенность сохранения спроса на продукцию (интернет-магазины, интернет-поисковики, производители сложной ультрамодной техники, фармацевтические).

Исследования компании Ibbotson Associates свидетельствуют, что бета-коэффициенты компаний характеризуются большей волатильностью, чем отраслевые уровни, поэтому систематический риск, присущий конкретной компании, может быть достаточно хорошо аппроксимирован с помощью отраслевого бетакоэффициента. Компания Ibbotson Associates для снятия проблемы нестабильности бета-коэффициента для отдельных компаний использует прием «отраслевого уровня». Компания Ibbotson Associates с определенной периодичностью (один раз в полгода) составляет справочники (таблицы) по отраслевым бетакоэффициентам согласно стандартной классификации отраслей экономики (standard industry classification, SIC). В рамках этой классификации компания относится к конкретной отрасли, если более 75% ее выручки приходится на соответствующий вид деятельности. Кроме того, таблицы Ibbotson Associates детализируются с учетом размеров компаний (чем меньше размер, тем выше при прочих равных значение бета-коэффициента), указывается медианное значение отраслевого бета-коэффициента, значения бета-коэффициента с учетом долгового финансирования и «очищенные значения» (unlevered beta). Приводятся также скорректированные значения бета-коэффициента, чтобы исключить искажения, связанные с наличием большого числа интегрированных компаний (в которых велики доли других сфер деятельности). Другие специализированные компании уточняют алгоритм отраслевого уровня на отраслевые сектора (фактически проводят регрессионный анализ подотрасли к рыночному портфелю). Цель — выделить индивидуальные риски подотрасли и рассчитать меру их систематического риска. На практике аналитики часто принимают отраслевой уровень за базу для оценки доходности сегментов внутри отрасли или же при отсутствии анализируемого сектора (отрасли) в специализированных таблицах, устанавливают значение бета-коэффициента на уровне единицы (как среднерыночный риск).

В ряде случаев используется формула средневзвешенных значений из расчетного регрессионным методом и отраслевого значений бета-коэффициента. Чем выше значение ошибки в регрессионном уравнении, тем весомее становится отраслевой коэффициент.

Прием отраслевого бета-коэффициента состоит в замене в САРМ значения «фактического» (сырого, рассчитанного регрессионным методом) бета-коэффициента на скорректированное, рассчитанное по отраслевым значениям. Йредпосылкой применения метода является выбор компанией целевой структуры капитала по отраслевым пропорциям.

Для аналитика рекомендуется следующий алгоритм:

• 1) определить отраслевую принадлежность компании;
• 2) по справочникам (базам данных) найти среднюю отраслевую величину бета-коэффициента или бета-коэффициента портфеля, составленного из компаний данной отрасли (сектора экономики);

• 3) сопоставить финансовый рычаг компании с отраслевыми значениями; при несовпадении скорректировать отраслевой бета-коэффициент на влияние финансового рычага. Алгоритм «очищения» отраслевого бета-коэффициента от эффекта финансового рычага и последующая корректировка для расчета предполагаемого бета-коэффициента для акционерного капитала компании приведены ниже. Это типичная, обязательная корректировка, которую используют аналитики. Часто можно увидеть и более детальные подходы к учету специфических характеристик компаний. Например, вводятся корректировки на операционный риск (операционный рычаг), размер, временной горизонт предполагаемого инвестирования;
• 4) скорректированное значение бета-коэффициента подставить в САРМ.

В аналитической практике для закрытых компаний, а также для бизнес-подразделений диверсифицированных компаний вместо фондового (регрессионного) метода оценки бета-коэффициента получили популярность методы:

• а) фундаментальных параметров (иначе называемый методом восходящего бета, включая и его модификацию — метод аналога (pure-play approach)) Р. Фуллера и Г. Керра;
• б) бухгалтерского бета, или учетный метод Хилла — Стоуна (1980 г.).

Основные различия трех указанных методов показаны на рис. 6.11.

Регрессионный метод расчета бета-коэффициента — нахождение тангенса угла наклона прямой из регрессионного уравнения, увязывающего доходность акций компании (например, дневные или недельные данные) с доходностью фондового индекса^[1]. Получаемый в результате коэффициент — «сырой бета» (raw beta). Степень достоверности этой меры риска отражает коэффициент де;

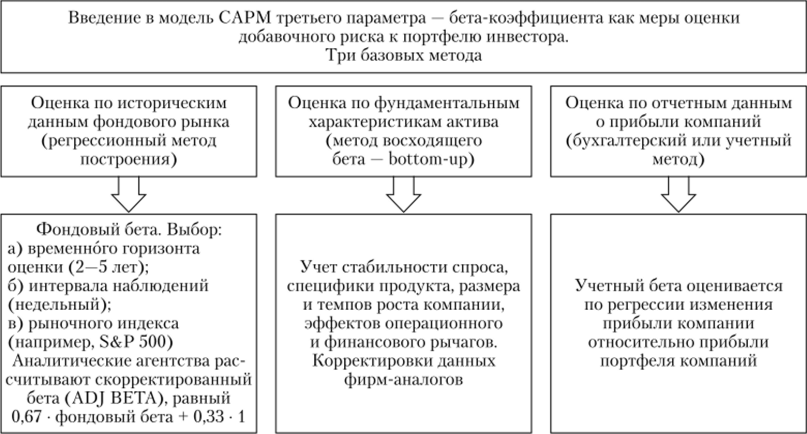
Рис. 6.11. Конструирование бета-коэффициента по фундаментальным характеристикам влияния.

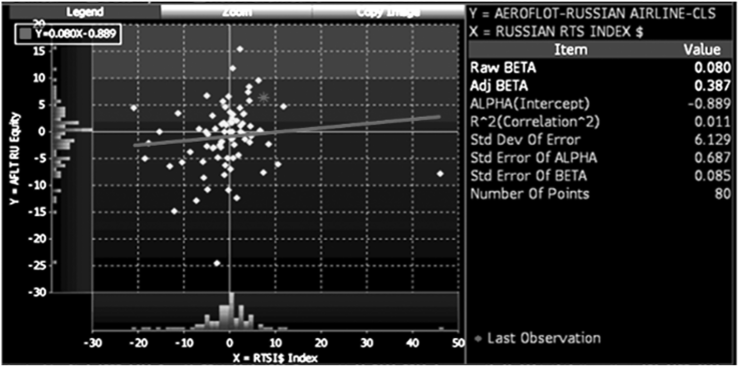
Рис. 6.12. «Книга бета» для акций «Аэрофлота».

терминации регрессионного уравнения (К²). Аналитики редко используют «сырой бета» в САРМ, так как он отражает прошлый систематический риск акции. Чтобы перейти к будущим оценкам, применяется поправка Маршалла Блюма, когда «сырой бета» принимается с весом 2/3, а «единичный бега» — с весом 1/3. Полученный скорректированный бета (стандартное обозначение adj beta) аналитики вводят в САРМ^[2]. Традиционно аналитические агентства (Thomson Reuters, Bloomberg и др.) показывают не только значение «сырого бета», но и ряд параметров, характеризующих полученную оценку, — аналитики видят «книгу бета» (коэффициент R², альфа, стандартные ошибки альфа и бета, число точек при построении регрессии). Пример «книги бета» по компании «Аэрофлот», представленной в терминале Bloomberg,, показан на рис. 6.12.

Разные аналитические агенства используют собственные коррекции и методики при расчете бета-коэффициента (не все вводят поправку М. Блюма). Поэтому на один момент времени аналитик может увидеть различные (но не сильно отличающиеся) значения по анализируемой компании. Например, на 12 февраля 2003 г. по компании CocaCola аналитики давали следующие оценки бета: Yahoo.finance — 0,29; Datastream — 0,37; Reuters — 0,42; Bloomberg — 0,64.

Метод фундаментальных параметров предполагает построение регрессионных зависимостей бета-коэффициента и отдельных фундаментальных характеристик деятельности компании, фиксирующихся в стандартной отчетности. Исходной информацией для анализа являются отчетные финансовые данные — отчет о прибыли и баланс. Статистический анализ показывает, что компании с высоким дивидендным выходом характеризуются низким значением бета-коэффициента. Этот факт вполне объясним, ведь высокие дивиденды характерны для стабильных компаний, имеющих высокую репутацию и устойчивое положение на рынке. Естественно предположить, что высокая волатильность прибыли характеризует компании с высоким значением бета-коэффициента. Серия исследований выявила зависимость между бета-коэффициентом и рядом фундаментальных показателей. А. Дамодаран демонстрирует зависимость по пяти ключевым переменным: дивидендной доходности DY; коэффициенту вариации CV (или стандартное отклонение)^[3] операционной прибыли; размеру компании ТА (активы всего); финансовому рычагу, определяемому как D/S темпу роста прибыли на акцию gEPS:

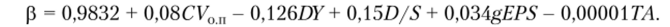
Объяснительная способность построенной регрессии вполне приемлема для практического использования.

Пример 6.9. Для малой нефтяной компании США бета-коэффициент по методу фундаментальной регрессионной зависимости будет оценен следующим образом:

• • CV — 2,6 млн долл.;
• • дивидендная доходность — 4% (коэффициент в уравнении равен 0,04);
• • соотношение между заемным и собственным капиталом — 0,1;
• • прогноз роста добычи нефти и чистой прибыли — 3% в год (коэффициент

в уравнении равен 0,03);

• активы по балансовой оценке — 10 млн долл.

Рассчитать бета-коэффициент.

Решение'.

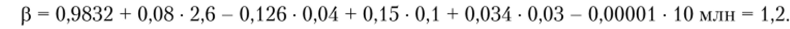
Метод аналогов является развитием приема отраслевого бета-коэффициента для ситуации существования явных аналогов на рынке с высокой достоверностью расчета бета-коэффициента регрессионным методом по ним. Предполагается, что отраслевые бета-коэффициенты могут быть неприменимы из-за диверсифицированное™ бизнеса анализируемой компании.

Метод аналога Фуллера — Керра предполагает следующий алгоритм: подбирается компания, акции которой торгуются на бирже и которая функционирует в том же направлении бизнеса или в тех же пропорциях включает в себя различные бизнес-единицы, что и анализируемая компания (подразделение или проект). По компании-аналогу бета-коэффициент рассчитывается регрессионным методом с возможными корректировками. При наличии нескольких аналогичных фирм используется медианное или средневзвешенное значение бета-коэффициента с учетом объема деятельности или величины активов.

Так как базовыми детерминантами бета-коэффициента являются структура издержек (операционный рычаг) и структура капитала (финансовый рычаг), то при наличии расхождений с аналогом по этим параметрам предложены различные корректировки. Эти корректировки строятся на различных предположениях о модельной зависимости стоимости компании с финансовым рычагом (V{_ei) и стоимости безрычаговой компании (V_unj_ev). Более подробно соотношение стоимостей рычаговой и безрычаговой компаний рассмотрено в гл. 7. В данной главе представлены формулы, которые вытекают из моделей соотношения стоимостей для увязки бета-коэффициента акции рычаговой и безрычаговой компаний.

Метод бухгалтерского бета, или учетный метод Хилла — Стоуна, будет рассмотрен далее.

Взаимосвязь рычагового бета-коэффициента акции с бета-коэффициентом акции компании, работающей исключительно на собственных средствах.

Важное исходное положение для моделирования зависимости бета-коэффициента от финансового рычага: с ростом долга риск собственника растет, следовательно, должна расти и требуемая доходность инвестирования. Это положение можно продемонстрировать на следующем примере.

Пример 6.10. Ожидаемый операционный денежный поток (OCF) компании равен 100 д. е., но с учетом бизнес-риска может измениться на 20%, т. е. денежный поток может стать как 80, так и 120 д. е. Компания работает на заемном капитале и ежегодно платит 70 д. е. в виде процентов. В зависимости от развития событий денежный поток собственникам (CFE) примет значения, приведенные в табл. 6.14 (налогом на прибыль можно пренебречь).

Таблица 6.14

Денежные потоки.

Таким образом, изменение операционной прибыли на 20% приводит к волатильности денежного потока собственникам в 66,5% (на 2/3 падает и растет поток собственнику при отклонении ситуации от базового сценария).

Различные предположения о факторах, определяющих справедливую стоимость рычаговой (левереджированной) компании, и характеристиках внешней среды, а также о финансовом положении самой компании (например, традиционные предположения о совершенном рынке капитала с наличием налога на прибыль и безрисковым корпоративным долгом компании) порождают разные модели, показывающие, как влияет финансовый рычаг на бета-коэффициент акции. Исходная конструкция, позволяющая получить увязку бета-коэффициента акций (собственного капитала) с бета-коэффициентом активов компании (без использования финансового рычага), приведена на рис. 6.13. Главное положение схемы — аналитический баланс компании — включает в себя активы, сформированные исключительно собственным капиталом, и выгоды налогового щита; привлеченный капитал состоит из собственного (Е) и заемного (D). Такое разложение следует из метода представления справедливой стоимости «по частям» с выделением операционных и финансовых выгод (см. гл. 5). Соответственно систематический риск двух элементов активов и двух элементов привлеченного капитала может быть оценен через четыре бета-коэффициента:

• 1) Рил — бета-коэффициент акций безрычаговой компании = бета-коэффициент активов компании;
• 2) Р/.' — бета-коэффициент акций рычаговой компании;
• 3) Pd ^— бета-коэффициент долга;
• 4) Рух — бета-коэффициент денежных потоков в виде налогового щита.

Делая разные предположения о рискованности налогового щита и заемного капитала, получаем разные выражения, увязывающие бета-коэффициенты активов и акций (собственного капитала) рычаговой компании.

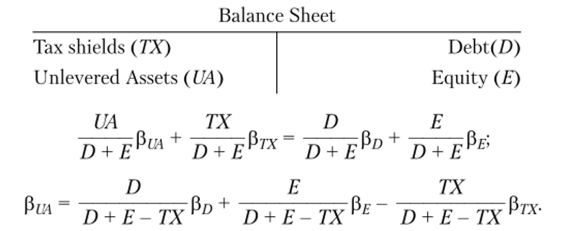
Рис. в. 13. Ключевые соотношения мер риска по активам и элементам привлеченного капитала компании.

Пример 6.11. Если долг является безрисковым, бета-коэффициент налогового щита равен нулю и приведенная оценка налогового щита (PVTS) может быть выражена как произведение долга на ставку налога на прибыль (D • Г), то из схемы (см. рис. 6.13) получаем следующее выражение для бета-коэффициента собственного капитала (Р/_Ст = Pf) и бета-коэффициента активов (р_л = р_м«/_ег):

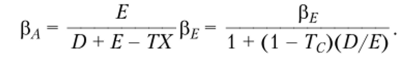
Другие возможные предположения относительно систематического риска налогового щита:

• • бета-коэффициент налогового щита равен бета-коэффициенту активов (безрычаговому бета-коэффициенту активов);
• • бета-коэффициент налогового щита равен бета-коэффициенту долга;
• • бета-коэффициент налогового щита меньше нуля.

Комментарии по этим положениям приведены в гл. 7.

В данном параграфе покажем различные модельные конструкции для рычагового бета-коэффициента рi_ev =f (…D/S) и продемонстрируем популярный алгоритм реализации модели на практике (табл. 6.15).

Таблица 6.15

Выражения рычагового бета, предложенные в академических работах в рамках корпоративных финансов

¹ Приведенная стоимость налогового щита есть функция ежегодных налоговых выгод и ставки дисконтирования для безрычаговой компании (k_u«i_ev).

Окончание табл. 6.15

Примечание. Т — ставка налога на прибыль; D — рыночная оценка долга; 5 — рыночная оценка собственного капитала; D/S — финансовый рычаг; k_fj — требуемая доходность по заемному капиталу; VTS — приведенная оценка налогового щита (по годам).

На практике часто можно увидеть использование финансовыми аналитиками совсем простой формулы:

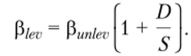
Пример 6.12. Сравним результаты, полученные по двум методам расчета бстакоэффициеита (1 — часто используемый практиками метод, 2 — метод Таггарта (1991 г.)), компаний, работающих на заемном капитале. Используем данные за 2007 г. для двух российских компаний: ОАО «Мосэнерго» и ОАО «Уралсвязьинформ» (бетакоэффициент акций принимается за единицу), расчет бета-коэффициента долга представлен в табл. 6.16, финансовый рычаг фиксируется по усредненным данным финансовой отчетности.

Таблица 6.16

Оценки «сырого» бета-коэффициента долга за период 2006—2010 гг.

Примечание. Расчет по рядам дневных доходностей относительно доходности индекса ММВБ:

• (1) p_lev = р,/1 +D/E)
• (2) p_/№ = p_M + (p_w-p,_/)D (l-r)/?

Для ОАО «Мосэнерго»:

• (1) р_/ет, = р,/1 + D/E) = 1(1 + 0,25) = 1,25;
• (2) р_!ev = р_м + (р_м — р₍,)D ( 1 — Т)/Е = 1 + (1 — 0,15) • 0,25 = 1,2125.

Для ОАО «Уралсвязьинформ»:

• (1) р_/№ = р,/1 + D/E) = 1 (1 + 1,42) = 2,42;
• (2) р_/№ = р_м + (Р_и — p,/)D (l — Т)/Е= 1 + (1 — 1,22) • 1,42 = 0,5456.

Приведенные расчеты показывают, что учет систематического риска заемного капитала существенно меняет оценку риска акций и, соответственно, требуемую доходность, но собственному капиталу.

Покажем реализацию алгоритма расчета бета-коэффициента по данным компании-аналога или отраслевому бета-коэффициенту, предложенного А. Дамодараном.

• 1. Нивелировать финансовый риск по компании-аналогу или отраслевому бета-коэффициенту (операция «очищения»). Простейшая формула при предположении о том, что бета-коэффициент долга равен нулю, позволяет провести эту корректировку и перейти от рычагового бета-коэффициента (рi_ev) к безрычаговому (unlevered beta) — fi_uni_€V.
• 2. Нивелировать эффект операционного рычага по аналогу, уже очищенному от финансового риска, и получить «фундаментальный бета». Эффект учитывается по соотношению постоянных (FC) и переменных (VC) издержек.
• 3. Ввести нагрузки по операционному и финансовому риску для анализируемой компании на «фундаментальный бета»:
  • а) нагрузка на операционный риск, т. е. бета-коэффициент анализируемой компании,

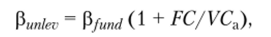
где Рf_und — «фундаментальный бета»; УС_а — переменные издержки аналога;

б) нагрузка на финансовый рычаг, т. е. «рычаговый бета» анализируемой компании,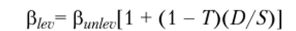

или.

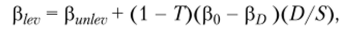
где р?> — бета-коэффициент долга.

В литературе полученное значение бета-коэффициента из отраслевой базы или из значений бета-коэффициента по компаниям-аналогам называется «восходящий бета». Учитываемые характеристики и алгоритм применения метода «восходящего бета» показаны на рис. 6.14.

На практике часто используется упрощенная поправка к безрычаговому бета-коэффициенту для отражения финансового риска с игнорированием ставки налога на прибыль:

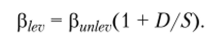
Здесь следует оговорить требования к компаниям-аналогам в одной отрасли, предъявляемые в финансовом анализе. Корректно подойти к отбору позволяет табл. 6.17.

Заметим, что в рамках одной отрасли компании могут существенно различаться по стадии жизненного цикла, качеству управления, степени диверсификации продукции, географической диверсификации. Метод аналогов позволяет эти нюансы отразить.

Пример 6.13. Попытаемся оценить бета-коэффициент частной фирмы, которая поставляет диагностическое оборудование для нефтегазовых компаний России.

Предполагается, что владельцы капитала компании являются диверсифицирован;

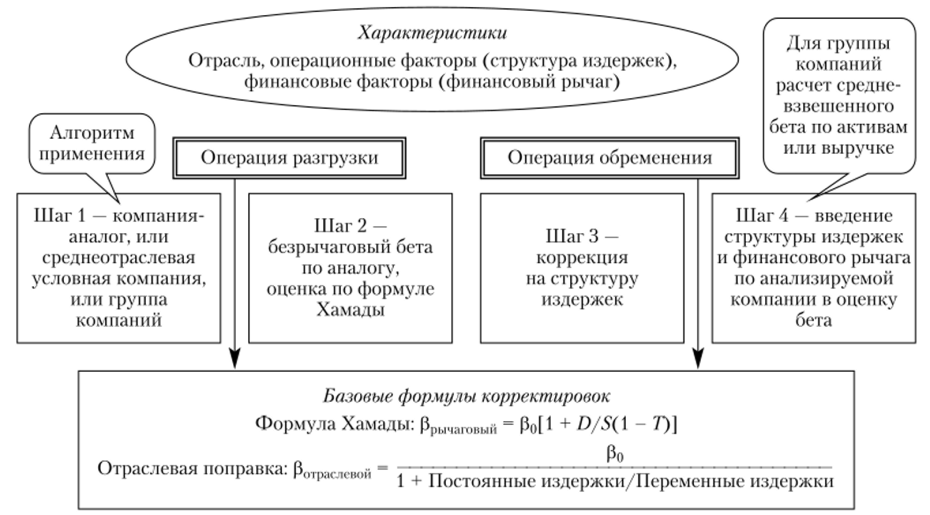
Рис. 6.14. Фундаментальные характеристики рыночного риска компании

и метод «восходящего бета»

Таблица 6.17

Выбор компании-аналога для расчета меры систематического риска

ными инвесторами. Фирма работает па финансовом рычаге, равном 0,1 (балансовое значение D/S), эффективная ставка налога на прибыль равна 20%. Бета-коэффициены торгуемых фирм США, занимающихся поставкой аналогичного оборудования, приведены в табл. 6.18.

Таблица 6.18

Бета-коэффициенты торгуемых фирм США.

Примечание. Эффективная ставка налога на прибыль — 40%.

Предполагается, ч то, но величине активов и структуре издержек рассматриваемые фирмы идентичны анализируемой компании.

Безрычаговый бета-коэффициент фирм-аналогов:

1,22/(1 + 0,6 0,2) = 1,09.

Бета-коэффициент для закрытой российской фирмы:

1,09(1 +0,8 — 0,1) = 1,18.

Получим следующую оценку требуемой доходности с упрощенным введением премии за страновой риск и премии за размер:

Используемая формула предполагает возможность работы компании на безрисковом заемном капитале. Такое предположение существенно завышает риск и требуемую доходность по собственному капиталу.

Метод бухгалтерского бета, или учетный метод Хилла — Стоуна, базируется на построении регрессионной зависимости между бухгалтерскими значениями доходности бизнеса или инвестиционного объекта (ROC, ROE) и показателями отдачи на капитал по фондовому индексу (портфелю компаний). Коэффициент регрессионного уравнения принимается за учетный бета-коэффициент.

Этот метод ориентирован на закрытые (непубличные) компании и разнообразные инвестиционные объекты (например, на коммерческую недвижимость). Бета-коэффициент рассматривается как фактор чувствительности бухгалтерских показателей отдачи от индикаторов доходности капитала по портфелю активов, доступному для инвестора.

Данными по компании обычно выступают исторические значения доходности активов, рассчитанные как отношение скорректированной на налог операционной прибыли к величине задействованного капитала (активов) по отчетпости. В качестве рыночной доходности принимается средневзвешенное значение бухгалтерской доходности активов всех компаний, участвующих в анализе.

Развитием метода может выступать оценка бета-коэффициента по динамике прибыли компании по отношению к средней прибыли группы.

Если значение бухгалтерского бета-коэффициента больше единицы, то это означает, что прибыль компании выросла на большую величину по отношению к прибыли сравниваемых компаний и наоборот. Бухгалтерский бета-коэффициент равен единице, если прибыль компании растет (надает) пропорционально прибыли других компаний.

Пример 6.14. Рассмотрим динамику прибыли технологической компании США Singapoll но кварталам в 2010 и 2011 гг. (табл. 6.19).

Сопоставление роста прибыли компании и рынка (прибыль по группе компаний, входящих в индекс S&P 500).

Таблица 6.19

Тангенс угла наклона регрессионной зависимости равен 2,2. Метод учетного бета-коэффициента предполагает принятие этого значения в качестве бета-коэффициента технологической компании.

Пример 6.15. Строительная компания, занимающаяся прокладкой коммуникаций для нефтегазовой материнской компании, является закрытым акционерным обществом и не имеет аналогов среди компаний открытого типа, котирующих акции на бирже. Аналитики определяют бухгалтерский бета-коэффициент по динамике прибыли данной компании и «усредненной» компании, имеющий усредненные параметры, рассчитанные по компаниям, входящим в биржевой индекс данной страны (табл. 6.20).

Таблица 6.20

Данные для расчета учетного бета-коэффициента.

Примечание. Оценка регрессионного уравнения: учетный (бухгалтерский) бета-коэффициент равен 2,44.

Аналитики развитых рынков капитала доказывают, что для моделирования доходности инвестирования, например, в малые страны Европы (Австрия, Швейцария) не обязательно проводить анализ характеристик этих стран. Достаточно руководствоваться «глобальной» версией САРМ.

Глобальная САРМ (global САРМ, GCAPM) — это конструкция формирования параметров модели САРМ для отдельной страны по данным глобального рынка капитала (отражается при показателях нижним индексом «д»).

Например, безрисковая ставка ищется на базе информации глобального рынка (как усредненное значение доходности портфеля государственных облигаций стран наивысшего кредитного рейтинга). Рыночная премия за риск также рассчитывается по данным глобального рынка. Бета-коэффициент оценивается регрессионной моделью по котировкам акций рассматриваемой компании локальной страны с глобальным индексом (например, S&P 500, MSCIGlobal). Бета-коэффициент для закрытых компаний определяется либо по методу аналогов, либо на базе отраслевого уровня, оцененного для портфеля компаний мирового рынка.

Глобальная версия САРМ.

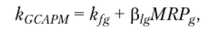
где kf_g — безрисковая ставка доходности на глобальном рынке; (3/_g — бета-коэффициент акции как мера систематического риска финансового актива рассматриваемой компании, которая рассчитана по чувствительности доходности акций данной компании на локальном рынке по отношению к динамике доходности глобального фондового индекса; MRP_g — рыночная премия за риск глобального рынка как разность между усредненной рыночной доходностью глобального рынка и средней безрисковой ставкой. Диапазон значений премии за риск глобатьного рынка — 3,2—5%.

Модели требуемой доходности акционерного капитала для развивающихся рынков капитала Для развивающихся рынков характерны высокая концентрация собственности, низкая ликвидность фондового рынка, наличие существенных транзакционных издержек, политические риски^[8]. Ввиду наличия высокой корреляции между развивающимися рынками и глобальным рынком капитала эти риски не устраняются диверсификацией у глобального инвестора. Еще одна проблема развивающихся рынков — отсутствие стационарности и динамичные изменения, связанные с либерализацией локальных рынков капитала с 1990;х гг.

В ряде академических работ предложены модификации конструкции САРМ, учитывающие особенности функционирования развивающихся рынков капитала. Некоторые модификации нашли применение в практике проведения фундаментального анализа^[9].

Глобальная модель плохо применима для развивающихся рынков. Риск и доходность инвестирования на развивающихся рынках (emerging markets) имеют два компонента: систематический риск относительно некоего приемлемого для инвестора портфеля и сохраняющийся несистематический риск. Причины сохранения несистематического риска могут быть разными:

• 1) политические риски, когда результаты инвестирования будут существенно зависеть от политических факторов (преемственности курса при смене правительства, наличия конфликтов в среде элиты страны и т. п.);
• 2) низкая ликвидность^[10];
• 3) малые размеры компаний, низкая их рыночная оценка и соответствующая высокая зависимость от внешней среды и спекулятивных поведений инвесторов^1[11].

Особенность развивающихся рынков — сегментирован! юсть (изолированность от мирового рынка), т. е. наличие барьеров на движение капитала. Эти барьеры не позволяют инвестору диверсифицировать капитал и сохраняют специфические риски в ожидаемой доходности. В результате на локальном рынке складываются собственные закономерности формирования цен финансовых активов.

Для сегментированных рынков капитала (segmented market) с высокой ликвидностью фондового рынка и наличием информации для обоснования безрисковой ставки и рыночной доходности (наличие для инвестора возможности диверсифицировать на рынке капитал) приемлема так называемая национальная, или локальная, версия САРМ. Если данные локального рынка не отвечают требованиям полноценного анализа систематического риска (бета-коэффициент акций), то эта версия не даст адекватной оценки доходности инвестирования.

Локальная САРМ (local САРМ, LCAPM) — это конструкция формирования параметров модели САРМ исключительно по данным локального (национального) рынка капитала.

Локальная версия САРМ.

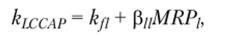
где kfi — безрисковая ставка доходности на локальном рынке (как доходность суверенных бумаг); р// — бета-коэффициент акции, рассчитанный регрессионным методом по индексу локального рынка или методом аналогов по регрессионным бета-коэффициентам компаний — аналогов данного рынка; MRP) — рыночная премия за риск на локальном рынке как разность между усредненной рыночной доходностью рассматриваемого рынка и средней ставкой государственных ценных бумаг или депозитов высоконадежных банков.

Если за минимальную ставку доходности принимается безрисковая доходность глобального рынка, то локальная САРМ принимает вид.

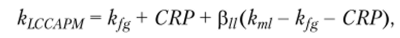
где CRP (country risk premium) — премия за страновой (политический) риск; k_mi — рыночная доходность на локальном рынке.

Влияние сегментированное™ рынка на уровень требуемой доходности инвесторов исследовал К. Харви^[12]. В ряде его работ доказывается, что требуемая доходность инвестирования на сегментированных рынках будет выше, чем на интегрированных, так как инвесторы потребуют большей компенсации за то, что они несут локальный, идиосинкратический риск. Это положение предполагает, что любое увеличение в степени интеграции рынков капитала должно привести к снижению требуемой доходности инвесторов и затрат на собственный капитал компаний. Р. Штульц^[13] предложил диагностирующие параметры, позволяющие включать в модель «риск — доходность» глобального инвестора премию за страновой риск. По его утверждению, с позиции глобального инвестора следует учитывать две характеристики: степень интеграции рынков (наличие барьеров в движении капитала) и ковариацию доходности на локальном и глобальном рынках. Характеристика формальных и неформальных барьеров в движении капитала, наблюдаемых на сегментированных рынках, дана в работе А. Серра (2003 г.)^[14].

Доказательством значимости такой характеристики, как сегментированность, являются исследования влияния либерализации рынка капитала на ожидаемую и требуемую доходность. Например, Г. Бекарт и К. Харви^[15][16], базируясь на модели дивидендной доходности (модель Гордона), показывают, что либерализация сегментированных рынков капитала приводит к сокращению затрат на собственный капитал в среднем на 50%. Аналогичное исследование на базе анализа изменений в дивидендной доходности и в темпах роста по 20 развивающимся рынкам (стран Южной Америки, Азии и Африки) представлено в работе П. Генри^[14]. Внешним признаком либерализации автор выбрал дату, когда иностранные инвесторы получают возможность покупать акции компаний локального рынка. В работе показано снижение затрат на капитал в результате либерализации в среднем почти на 50%.

В работе Г. Бекарта и К. Харви 1995 г.^[18] предлагается рассматривать требуемую доходность частично сегментированного рынка как взвешенную комбинацию оценок для глобального рынка и полностью сегментированного национального. Веса должны зависеть от степени изолированности. Например, если уровень сегментации оценен по весовой шкале в w, а уровень открытости как (1 — w), результирующая доходность может быть представлена следующим образом:

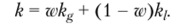
Это простейший вариант моделирования доходности для сегментированных рынков.

Stulz R. Globalisation, corporate finance, and the cost of capital / R. Stulz // Journal of Applied Corporate Finance. 1999. Vol. 36. P. 8—25.

Однофакторная модель учета политического риска — модель К. Эрба, К. Харви и Т. Висканты (EHV)^[19] акцентирует внимание на политические риски развивающихся стран, которые, по мнению авторов, являются определяющими в формировании требуемой доходности^[20]. Авторы предполагают оценивать предельную требуемую доходность (нижняя граница) инвесторов развивающихся рынков по регрессионной зависимости относительно построенного странового рейтинга. Ключевое предположение модели EIIV — сегментированность развивающихся рынков (наличие барьеров на движение капитала).

Модель EHV актуальна для стран со слабым фондовым рынком, не позволяющих применить модификации в рамках конструкции САРМ. Авторы модели EHV предлагают собственную методику построения рейтинга, учитывающую пять финансовых, 13 политических и шесть экономических факторов риска страны. Полученные баллы по каждому фактору формируют композитный рейтинг страны и в определенной степени соответствуют признанным кредитным рейтингам агентств (например, S&P).

Страновой кредитный риск. Страновой кредитный риск (country credit risk, CCR) — это построенная балльная оценка риска страны, учитывающая политические, экономические и финансовые риски.

Принципиально идея модели сводится к следующей зависимости:

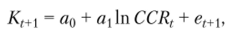
где й₀, ci — расчетные коэффициенты регрессионного уравнения; e_t+1 — свободный член.

Например, при анализе 135 стран за ряд лет авторы модели EHV оценили следующую регрессию:

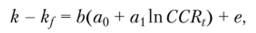
где (k — kf) — премия за страновой рыночный риск, т. е. средний риск владения собственным капиталом в стране; Ь, а₀, — расчетные параметры регрессии;

In CCR, — натуральный логарифм определенного авторами значения кредитного рейтинга страны в году t.

Полученные авторами модели EHV оценки премии за риск следующие: а₀ = = 53,17, коэффициент чувствительности a_t —10,47. Значение коэффициента а 1 отрицательно, так как более высокий страновой рейтинг гарантирует пониженную доходность.

Натуральный логарифм вводится для отражения нелинейной зависимости доходности от странового рейтинга — при низких рейтингах премия за риск существенно возрастает. По оценке авторов модели EIIV, уровень кредитного рейтинга страны объясняет 16% изменений в средней доходности и до 40% волатильности доходности, что гораздо существеннее, чем дивидендная доходность, которая практиками в ряде случаев выбирается как приближенная оценка требуемой доходности.

Различные версии САРМ, используемые аналитиками для моделирования требуемой доходности на акционерный капитал на развивающихся рынках, сиТаблица 6.21

Модификации САРМ в зависимости от степени интеграции и качества развития локальных рынков капитала

стематизированы в табл. 6.21Ч Если отсутствует приемлемый для аналитики локальный рынок ценных бумаг, то аналитики могут использовать модель Эрба — Харви — Висканты.

Гибридные версии САРМ — это попытка интегрировать принципы ценообразования финансовых активов по однофакторной модели компенсации систематического риска на развивающихся рынках с данными, формируемыми на развитом рынке капитала. Трансформации подвергаются все параметры САРМ: безрисковая ставка, премия за рыночный риск, расчет бета-коэффициента. Часто за основу построения гибридных моделей берутся следующие данные: MRP_VS — рыночная премия за риск на рынке США (оценивается либо по историческим данным, либо гипотетическим методом как вмененная оценка); — бета-коэффициент высоколиквидных компаний-аналогов, рассчитанный по данным глобального рынка.

Ключевой параметр, требующий отражения по развивающимся рынкам, — не устраняемый диверсификацией политический, или страновой, риск. Для корректного отражения странового риска следует выделить его факторы и понять степень влияния на отдельные компании и рынок в целом (поведение фондового индекса).

Основные факторы странового риска России приведены ниже.

• 1. Неопределенность применения законодательства (правоприменение) п администрирования нормами налогообложения.
• 2. Административное давление на малый и крупный бизнес:
  • • централизация политической системы и президентской власти;
  • • персонализация отношений бизнеса и государства;
  • • концентрированная структура экономики и фондового рынка;
  • • слабая банковская система, с трудом преодолевающая панические настроения населения;
  • • слабость общественных институтов.
• 3. Наличие большого нерыночного сектора в экономике. CRP — страновая премия за риск, количественно учитывающая систематическое влияние политических факторов риска и рисков слабости фондового рынка для развивающихся экономик. Предполагается, что все оценки проведены в долларовом эквива- ^1[21]

ленте (цены акций в долларах для расчета доходности). Для применения к денежным потокам в валюте локального рынка требуется корректировка. Для развитых рынков CRP равна нулю (при интегрированности в глобальный рынок капитала и низкой корреляции с глобальным рынком). Значение CRP может определяться по спреду доходности государственных ценных бумаг локального и глобального рынков. Различают суверенный спред и типичный спред дефолта.

Суверенный снред дефолта — разность между доходностью государственных ценных бумаг одного срока локального и глобального (например, США) рынков.

Типичный спред дефолта отражает премию к безрисковым инструментам по государственным заимствованиям мирового рынка как усредненную оценку. Характеризует определенный уровень кредитного риска страны.

Скорректированная локальная САРМ

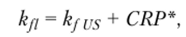
где CRP* — типичный спред дефолта (по кредитному рейтингу ряда стран и наблюдаемых доходностях государственных бумаг по ним).

Страновая премия за риск может также встраиваться в рыночную премию или в премию за риск конкретного инвестиционного варианта. Эти версии будут прокомментированы далее.

На практике применяют четыре метода количественной оценки страновой премии за риск: метод кредитного рейтинга, метод широкого инвестиционного рейтинга (типичный спред дефолта), метод фундаментальных факторов и метод относительной рискованности рынков акций (рис. 6.15).

Наиболее часто применяется метод кредитного рейтинга, когда оценка строится на наблюдаемом страновом спреде риска дефолта (риска невыполнения.

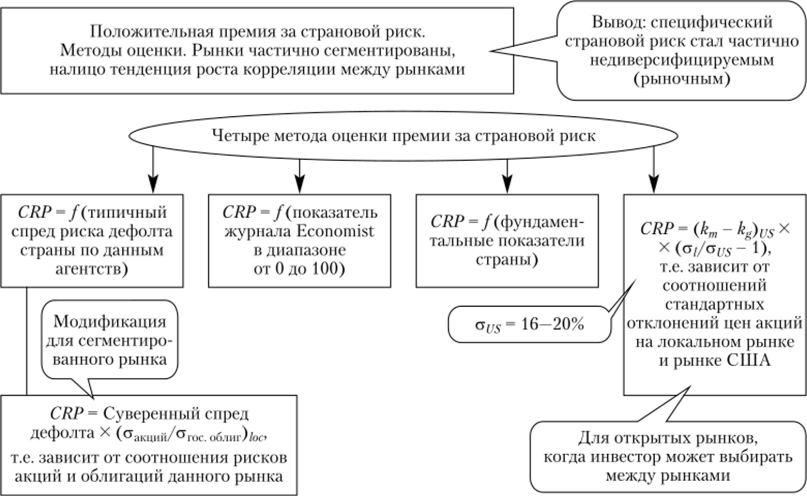
Рис. 6.15. Методы оценки положительной премии за страновой риск

государственных обязательств по заимствованиям). Необходимая информация — присвоенные кредитные рейтинги странам (например, агентствами S&P, Moody’s, Fitch) и наблюдаемые различия в доходности по государственным заимствованиям на локальных рынках и рынке США^[22][23]. Метод исходит из положения, что доходность государственных облигаций может рассматриваться как непосредственная мера странового риска. Такой подход, но сути, отождествляет страновые риски и риск суверенного дефолта.

Например, доходность еврооблигаций РФ с погашением в 2018 г. составляет 7,25%^{2 3 4 5}, а доходность соответствующего срока казначейских облигаций США — 2,64% (по данным на 23 марта 2009 г.). Таким образом, рыночный спред дефолта (как CRP) составляет 4,61%.

Типичный спред дефолта государственных заимствований представляет собой оценку усредненного значения суверенного спреда по странам с одинаковым рейтингом.

Например, если по Бразилии и Перу рейтинг S&P составляет ВВ-, а суверенные спреды равны 423 и 502 базовых пунктов соответственно, то типичный спред дефолта по рейтингу ВВ- будет принят на уровне 463.

Метод кредитного рейтинга задания страновой премии за риск. Этот метод основан на следующем алгоритме.

1. По странам рассчитывается суверенный спред риска дефолта:

• 2. Систематизируется информация по присвоенным страновым кредитным рейтингам (табл. 6.22). Суверенный спред дефолта, как правило, отличен, но странам с одним значением рейтинга.
• 3. Рассчитывается типичный (усредненный) спред дефолта.
• 4. Метод рейтинга предполагает задание страновой премии за риск по значению типичного спреда. Например, для страны с рейтингом ВВ- премия за страновой риск будет рекомендована на уровне 4,63%.
• 5. Так как суверенные спреды постоянно меняются, отражая изменения макроэкономических параметров (спреды повышаются во время спада и понижаются в периоды экономического подъема), то ряд агентств рассчитывает устойчивые типичные спреды, сохраняющие значимость на относительно длительном временном промежутке. Одним из вариантов нахождения такой зависимости спреда от рейтинга являются регрессионные оценки по прошлым данным. Например, может использоваться регрессия спреда, но отношению к экономическому росту:

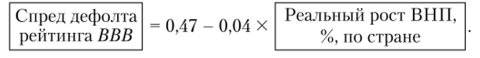
Примеры присвоенных страновых кредитных рейтингов приведены в табл. 6.23.

Страновые поправки с учетом кредитного рейтинга страны (для низких кредитных рейтингов — развивающиеся страны) на начало 2011 г.

Таблица 6.22

Таблица 6.23

Страновые кредитные рейтинги на конец 2011 г.

Пример 6.16. Если компания осуществляет свою деятельность в стране с кредитным рейтингом ВВВ и фондовый индекс страны не отражает широкую диверсификацию портфеля, то для задания премии за рыночный риск может применяться метод поправок с учетом табл. 6.22.

Пусть безрисковая доходность на рынке функционирования компании составляет 10%, бета-коэффициент аналогичной компании в США равен 1,1 (компания в той же отрасли, структура издержек и финансовый рычаг идентичны, т. е. компанию можно принять за полный аналог). Требуемая доходность по собственному капиталу компании k_s составит, %: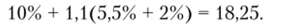

В данном примере страновая премия на риск корректируется на бета-коэффициент, т.с. предполагается, что факторы странового риска нс одинаково действуют на компании местного рынка.

Анализ страновых рейтингов и спреда доходности по государственным заимствованиям позволяет сделать интересные выводы по требуемой доходности компаний. По двум аналогичным компаниям Полыни и Болгарии (например, газораспределительные сети) требуемая доходность польской компании будет на два процентных пункта меньше, чем болгарской.

Недостаток метода кредитного рейтинга — акцентирование внимания только на кредитных рисках страны, хотя факторов специфического странового риска инвестирования в собственный капитал гораздо больше. Результат такого подхода — занижение страновой премии за риск. Для глобального инвестора, выбирающего из множества инструментов по странам, этим недостатком можно пренебречь. Для сегментированных рынков требуется модификация.

Модификация метода кредитною рейтинга — учет большего риска инвестирования в акции по сравнению с государственными заимствованиями (рис. 6.16).

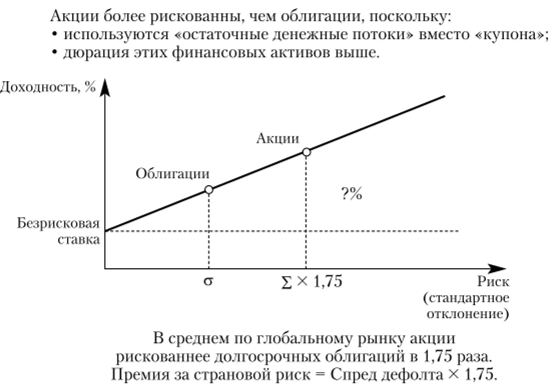
Рис. 6.16. Метод относительного риска акций

Для сегментированных рынков и в целях отражения большего числа факторов странового риска метод рейтинга рекомендуется модифицировать, вводя оценку изменчивости локального фондового рынка по отношению к суверенным заимствованиям. Логика такой модификации строится па превышении странового риска инвестирования в акции над страновым риском инвестирования в облигации.

Формула модифицированной премии за страновой риск на базе метода рейтинга такова:

Здесь стандартное отклонение отражает доходность соответствующего финансового актива (для фондового рынка — индекса, для государственных облигаций — заимствований длительного срока до погашения).

Стандартное отклонение, а рассчитывается в годовом исчислении по ценным бумагам (государственным облигациям и акциям) в долларовом эквиваленте.

Среднее соотношение волатильности рынков акций и облигаций для глобального рынка составляет 1,5, поэтому аналитики часто закладывают в расчет именно это значение. По российскому рынку часто закладывается в расчет значение 1,75.

Пример 6.17. Венесуэла в начале 2002 г. по шкале агентства Moodys имела рейтинг В2 и суверенный спред дефолта 538 базовых пунктов. По оценкам за 2001 г. стандартное отклонение фондового индекса акций страны (использовались дневные данные) в годовом исчислении составило 33%, а стандартное отклонение оцененных в долларах государственных облигаций — 16%. Модифицированная премия за страновой риск для Венесуэлы на базе метода рейтинговой оценки составит, %:

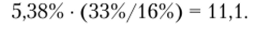
Данная оценка предполагает отсутствие возможности диверсифицировать страновые риски из-за высокой сегментированное™ рынка Венесуэлы.

Применение этого метода для российского рынка при спреде дефолта в 430 базисных пунктов на 2002 г. и стандартном отклонении в 35% в годовом исчислении (по индексу РТС) даст оценку премии за страновой риск, %:

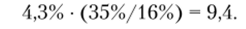
При снижении спреда к началу 2004 г. до 280—300 базисных пунктов премия за страновой риск по России составит 6,1%. Использование в качестве информационной базы анализа индекса ММВБ даст несколько иную оценку из-за пониженного значения стандартного отклонения (24% в годовом исчислении).

Для 2009 г. поправочный коэффициент по российскому рынку вырос до 4,383 (с^ртс/^гособлигаций ⁼ 54,58'/12,45 = 4,38). При суверенном спреде дефолта в 2,2% премия за страновой риск составит 2,2% • 4,38 = 9,6%.

Тогда 9,6% + 5% = 14,64% — полученная оценка средней рыночной премии за риск, когда в качестве развитого рынка выбран рынок США. Метод типичного спреда дефолта на 2009 г. дает более низкие оценки (2,5% + 5% = 7,5%).

Для глобальных инвесторов, использующих вложения на разных рынках, страновой риск может быть оценен по волатильности локального рынка по отношению к развитому рынку, например США. На таком включении в анализ относительного риска инвестирования строится четвертый метод, приведенный на рис. 6.15. Более высокое стандартное отклонение цен акций локального рынка должно компенсироваться для глобального инвестора более высокой страновой доходностью, что и отразит страновая премия за риск. Такой подход предполагает, что чем больше относительная волатильность локального рынка, тем выше премия за средний риск инвестирования на этом рынке.

Метод относительной рискованности локального рынка предполагает задание страновой премии за риск пропорционально риску локального рынка ак;

Стаидартное отклонение индекса РТС рассчитано на 6 марта 2009 г.

ций по сравнению с глобальным. Формула расчета премии за средний риск инвестирования в акции такова:

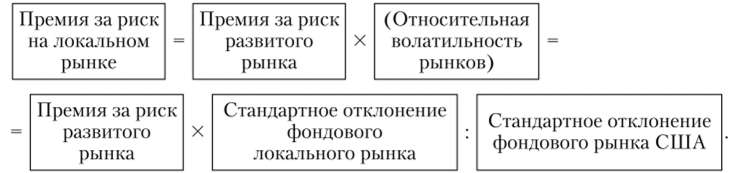
При этом а" = о₍-5 — показатель волатильности глобального рынка (global market index’s return volatility).

Стандартное отклонение фондового рынка США в докризисный период составляло порядка 20% (оценка в годовом исчислении). Оценки для развивающихся рынков находятся в диапазоне 30—45%.

Для расчета премии за страновой риск используют следующую формулу:

Здесь а/_ос — стандартное отклонение цен акций в долларовом исчислении на локальном рынке, показывающее риск инвестирования в акции страны.

Например, для российского рынка (2009 г.) премия за рыночный риск, %, определяется таким образом: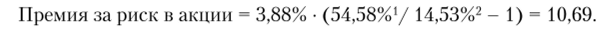

Данный метод показывает хорошие оценки, но имеет один существенный недостаток, связанный с характеристикой анализируемых фондовых рынков, — игнорирование рыночной ликвидности. При низкой ликвидности фондового рынка стандартное отклонение локального рынка может оказаться заниженным, что приводит к недооценке премии за страновой риск. По сути, метод исходит из сходной ликвидности по локальному рынку и рынку США. Развитием метода может стать введение поправок на ликвидность рынка.

Пример 6.18. Риск инвестирования в акции компаний Венгрии выше, чем риск инвестирования на рынке США, о чем можно судить, но значению годового стандартного отклонения венгерских акций, равному 38% (что превышает оценку для акций США — 20%). Если принять премию за рыночный риск на рынке США в 5,5% и не делать поправок на низкую ликвидность венгерского рынка, премия за средний риск инвестирования в компании Венгрии составит, %:

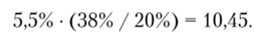
Премия за страновой риск Венгрии по методу относительных рисков будет равна 4,95%.

Применяются три принципиальных варианта для включения премии за страновой риск (как еще одного индикатора рыночного риска сегментирован^[24][25]

ного рынка) в оценку требуемой доходности: в корректировку безрисковой доходности, корректировку рыночной премии за риск и отдельный учет с фактором влияния X.

Модель Дамодарана (2002 г.) ставит влияние странового риска на доходность активов в зависимость от величины систематического риска этого актива:

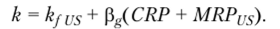
Предполагается, что страновой риск по компании пропорционален рыночному риску.

Особенности различного влияния политического риска на доходности отдельных акций и инвестиционных активов рассматривали многие исследователи^[26]. Попыткой модельно отразить эго влияние является двухфакторная модель Дамодарана с параметром X.

Двухфакторная модель Дамодарана (2003 г.) вводит индивидуальный фактор чувствительности актива к страновому риску (фактор X):

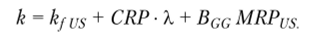
Параметр X (X Дамодарана) показывает степень влияния странового риска на компанию (например, по доле деятельности компании на внутреннем рынке относительно средней компании той же отрасли). Предложено несколько вариантов количественного задания параметра X.

Первый вариант задания X предполагает учет объема операций компании на внутреннем (локальном) рынке по сравнению со средними значениями. Чем больше объем операций, тем больше подверженность страновому риску. Для вычисления меры риска доля внутренних операций компании в общем объеме сопоставляется со средней долей типичной компании страны. Например, для российских компаний оценкой может выступать доля экспорта (Ех) у оцениваемой компании по отношению к среднему уровню экспорта по рынку. Коэффициент лямбда рассчитывается по формуле.

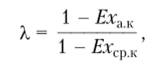
где Ех._лк — доля экспорта анализируемой компании; ?х_срк — доля экспорта средней компании страны.

Принимая долю экспорта по средней компании за 10%, получаем, что компании нефтяного сектора имеют оценку X в диапазоне 0,4—0,5. Эта оценка не учитывает риски претензий регулирующих органов, и для компаний, подпадающих под регулирующие меры, следует вводить еще одну поправку.

Второй вариант задания X предполагает построение двух регрессий: линейной регрессии доходности акций анализируемой компании по доходности суверенных государственных облигаций и регрессии фондового индекса страны, но суверенным государственным облигациям. Регрессия (угол наклона) но компании позволит получить индивидуальную оценку странового риска компании, т. е. оценку чувствительности данной компании к факторам странового^[27][28]

риска. Параметр А. равен соотношению углов наклона регрессий по анализируемой компании и по средней компании страны.

Модель Лессарда^[29] вводит поправку на страновой риск через учет относительной волатильности рынков капитала.

Исходная база для сопоставления — рынок США. Такой метод моделирования доходности использует, например, российская инвестиционная компания «Атон»:

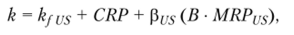
где p_f/s — бета-коэффициент аналога, но американским компаниям (оценка с учетом различий в финансовом риске); В — соотношение рисков по двум рынкам — отношение волатильности локального рынка к рынку США (отношение стандартных отклонений доходностей фондовых индексов). Например, В = ор_ТС/Os&p-

Такая модификация связана с тем, что расчет CRP по спреду доходности количественно отражает наличие страновых факторов риска в заимствованиях, но не в привлечении собственного капитала, который является более рискованным. Встраивание странового риска в виде спреда дефолта занижает уровень требуемой доходности по акциям локального рынка.

Модель Годфри — Эспинозы базируется на расчете бета-коэффициента и рыночной премии за риск по данным локального рынка с введением страновой премии за риск (CRP) в корректировку глобальной ставки безрисковой доходности. Для избежания двойного учета риска в модель вводится поправочный коэффициент 0,6 (как корректировка премии за риск в виде множителя (1 — R^[30]) в модели Перейро, где /г — коэффициент детерминации регрессионного уравнения, связывающего доходность компании на локальном рынке с изменчивостью премии за страновой риск).

Формула требуемой доходности компании развивающегося рынка согласно модели Годфри — Эспинозы^[30] принимает вид.

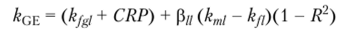
или.

где В — соотношение рисков по двум рынкам — отношение волатильности локального рынка к рынку США (отношение стандартных отклонений).

Этот параметр соответствует модели Лессарда. Корреляция между рынками предполагается равной единице. Коэффициент детерминации волатильности рынка акций относительно странового риска по заимствованиям считается постоянным на уровне 0,6 (это аналог (1 — /г) скорректированной локальной модели).

Скорректированная гибридная модель САРМ (adjusted hybrid САРМ, АН-САРМ) Л. Перейро (2001 г.) устраняет двойной учет странового риска в модели через использование произведения двух бега-коэффициентов, ориентированных на глобальный рынок, и поправки, отражающей значимость странового риска:

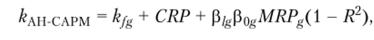
где Р— «страновой бета» как коэффициент регрессии между глобальным и локальным рыночными индексами (как тангенс угла наклона регрессии локального рынка акций к глобальному индексу); р₀д — среднее значение бета-коэффициента по сопоставимым компаниям на глобальном рынке (компании-аналоги); R² — коэффициент детерминации регрессионного уравнения между локальным рынком акций и страновым риском, т. е. доля волатильности локального рынка, которая объясняется страновым риском (вводится для устранения двойного учета риска). Рынок США может использоваться как аппроксимация глобального рынка.

Таким образом, в модели Перейро вводится корректирующий множитель (1 — R²), устраняющий проблему двойного учета странового риска. Значения (1 — R²) по развивающимся странам различны и колеблются от 0,56 (Аргентина) до 0,79 (Турция)¹. Для российского рынка расчетное значение на 2007 докризисный год составляло 0,48.

Пример 6.19. Систематический риск российского рынка (р_//;) относительно глобального (его индикатором выступал в расчетах индекс morgan stanly capital international, MSC1) был рассчитан T. В. Тепловой на основе данных РТС за 1993— 2002 гг. Параметр по российскому рынку относительно MSCI па 2003 г. оценен в 1,75. Стандартное отклонение доходности акций российских компаний в годовом исчислении при рассмотрении динамики недельных иен в долларах получено на уровне 35%. Как результат, средняя доходность инвестирования в акции компаний России — 11,5% годовых (в долларах). Для компаний, формирующих российский рынок («голубые фишки»), эта доходность может рассматриваться как требуемая (бета-коэффициент этих компаний близок к единице). Остальные компании являются более (менее) рискованными, но с учетом низкой ликвидности их доходность будет выше полученной оценки.

Бета-коэффициент также часто корректируется при реализации конструкции САРМ на развивающихся рынках капитала. Возникающие проблемы и методы корректировки отражены в табл. 6.24.

Необходимые корректировки при расчете бета-коэффициентов акций развивающихся рынков разными методами.

Таблица 6.24

Оценки на 2006 г.

• [1] Заметим, что количественные значения бета-коэффициента получаются одинаковыми, еслистроится регрессия по премиям за риск или по доходностям (доходность акций регрессируется надоходность индекса).
• [2] Такая поправка используется в базе Bloomberg.
• [3] Standard variation = SV= Standard deviation = SD = Стандартное отклонение.
• [4] Ставка для пересчета эффекта налогового щита в первый год равна k (j, а в последующие годы k unlev
• [5] Fernandez Р. WACC: Definition, Misconceptions and Errors. Madrid: IESE Business School, 2011. http://ssrn.com/abstract= 1 620 871.
• [6] Учет риска дефолта в отражении эффекта финансового рычага — Ruben D. Cohen (2007).
• [7] Учет риска дефолта в отражении эффекта финансового рычага — Ruben D. Cohen (2007).
• [8] Hoff К. After the Big Bang? Obstacles to the emergence of the rule of law in post-communist societies / K. Hoff, J. E. Stiglitz// American Economic Review. 2004. Vol. 94 (3). P. 753—763.
• [9] Комментарии по тестированию САРМ на развивающихся рынках капитала представленыв учебнике: Теплова Т. В. Инвестиции.
• [10] См., например: Bekaert G. Liquidity and expected returns: lessons from emerging markets /G. Bekaert, C. Harvey, C. Lundblad // Working Paper. Columbia University, Duke University andIndiana University, 2003.
• [11] См., например: Batry С. B. Robustness of size and value effects in emerging equity markets, 1985—2000/С. B. Barrv, E. Goldrever, L. Lockwood, M. Rodriguez// Emerging Markets Review. 2002. Vol. 3.P. 1−30.
• [12] Harvey С. R. Predictable risk and return in emerging markets / C. R. Harvey // Review of
• [13] Financial Studies. 1995. Vol. 8. P. 773—816: Haivey C. R. The risk exposure of emerging equity markets/ C. R. Harvey // World Bank Economic Review. 1995. Vol. 9. Iss.l. P. 19—50.
• [14] Cm.: Sena A. The Cross Sectional Determinants of Returns: Evidence from Emerging Market’sStocks / A Serra // Working Paper, University of Porto, Faculty of Economics Home Page. 2003. № 28. Oct.
• [15] Bekaert G. Foreign speculators and emerging equity markets / G. Bekaert, C. Harvey // Journal ofFinance. 2000. Vol. 55. Iss 2. P. 565—613.
• [16] Нету P. B. Capital-Account Liberalization, the Cost of Capital, and Economic Growth /P. B. Henry // The American Economic Review. 2003. Vol. 93. Iss 2. P. 91—96.
• [17] Cm.: Sena A. The Cross Sectional Determinants of Returns: Evidence from Emerging Market’sStocks / A Serra // Working Paper, University of Porto, Faculty of Economics Home Page. 2003. № 28. Oct.
• [18] Bekaert G. Time-varying world market integration / G. Bekaert, C. Harvey // Journal of Finance.1995. Vol. 50. P. 403−444.
• [19] Erb С. В. Country risk and global equity selection / С. B. Erb, C. It. Harvey, T. E. Viskanta //Journal of Portfolio Management. 1995. Vol. 21. № 2.
• [20] Erb C. Expected Returns and Volatility in 135 Countries / C. Erb, C. R. Harvey, T. Viskanta //Journal of Portfolio Management. 1996. Spring. P. 46—58.
• [21] Pereiro L. The valuation of closely-held companies in Latin / L. Pereiro // America EmergingMarkets Review. 2001. Vol. 2. P. 330—370.
• [22] Следует иметь п виду, что рейтинги присваиваются для заимствований в национальнойи иностранной вапюте.
• [23] www.cbonds.ru, по данным на 23 марта 2008 г.
• [24] Стандартное отклонение индекса РТС рассчитано на 23 марта 2009 г.
• [25] Стандартное отклонение индекса S&P 500 рассчитано па 23 марта 2009 г.
• [26] 2
• [27] См., например: Bailey IK Exchange rate fluctuations, political risk, and stock returns: some evidence from an emerging marke / W. Bailey, P. Y. Cluing // Journal of Financial and QuantitativeAnalysis. 1995. Vol. 30. P. 541 -563.
• [28] Damodaran A. Measuring company exposure to country risk: theory and practice / A Damodaran //Journal of Applied Finance. 2003. Vol. 13. P. 63—75.
• [29] См.: Lessard D. R. Incorporating country risk in the valuation of offshore projects / D. R. Lessard //Journal of Applied Corporate Finance. 1996. Vol. 9. P. 52—63.
• [30] Godfrey S. Practical Approach to Calculating Costs of Equity for Investments in EmergingMarkets / S. Godfrey, R. Espinosa //Journal of Applied Corporate Finance. 1996. Fall. P. 80—89.
• [31] Godfrey S. Practical Approach to Calculating Costs of Equity for Investments in EmergingMarkets / S. Godfrey, R. Espinosa //Journal of Applied Corporate Finance. 1996. Fall. P. 80—89.