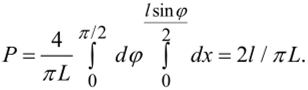Плотность вероятности двумерной случайной величины

Двумерная случайная величина (X, Y) называется непрерывной, если ее функция распределения F (x, y)~ непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная F (х, у).

Как и для одномерной случайной величины, введем понятие плотности вероятности двумерной СВ.

Оценим вероятность попадания случайной точки в прямоугольник со сторонами Ах и, А у. Средняя плотность вероятности в данном прямоугольнике равна отношению вероятности к площади прямоугольника Ах-Л у. Будем неограниченно уменьшать стороны прямоугольника, устремив Ах и А у к нулю. С учетом (5.9) получим:

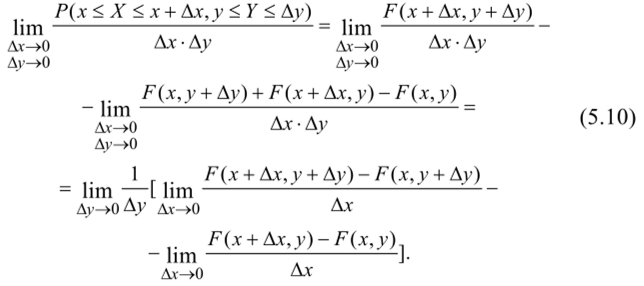
Учитывая то, что функция F (x, y) непрерывная и дифференцируемая по каждому аргументу, выражение (5.10) примет вид:

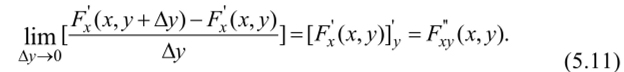
Плотностью вероятности (плотностью распределения, или совместной плотностью) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная частная производная ее функции распределения:

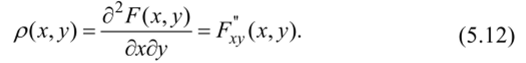
Плотность распределения двумерной СВ обладает свойствами, аналогичными свойствам плотности вероятности одномерной СВ:

1. Плотность распределения двумерной случайной величины есть неотрицательная функция, то есть

Это свойство вытекает из того, что F (x, y) — функция неубывающая по каждому аргументу.

2. Вероятность попадания непрерывной двумерной случайной величины (Х, У) в область D равна

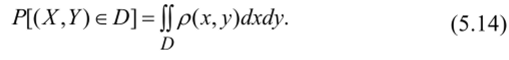
По аналогии с одномерной СВ, для двумерной СВ (X, Y) введем понятие «элемент вероятности», равный p (x, y) dxdy. Он представляет (с точностью до бесконечно малых более высоких порядков) вероятность попадания случайной точки в элементарный прямоугольник со сторонами dx и dy. Тогда вероятность попадания двумерной СВ в область D на плоскости Оху геометрически изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения р (х, у) и опирающегося на область D, а аналитически — двойным интегралом (5.14).

3. Функция распределения непрерывной двумерной случайной величины выражается через ее плотность вероятности по формуле:

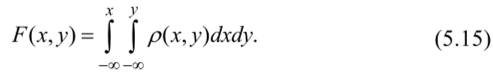
Функция распределения F (x, y) есть вероятность попадания в бесконечный квадрант D, который можно рассматривать как прямоугольник, ограниченный абсциссамиоо и х и ординатами — и у.

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной СВ равен единице:

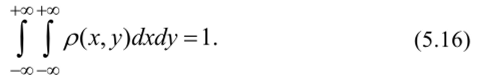
Несобственный интеграл (5.16) есть вероятность попадания во всю плоскость Оху, а вероятность достоверного события равна 1.

Зная плотность вероятности двумерной СВ (X, Y), можно найти функции распределения и плотности вероятностей ее одномерных составляющих X и Y. Учитывая (5.6) и (5.15), получим:

Дифференцируя функции распределения F,(x) и F₂(y) по аргументам х и у соответственно, получим плотности вероятности одномерных СВ:

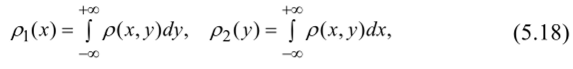
т. е. несобственный интеграл в бесконечных пределах от совместной плотности р (х, у) двумерной случайной величины по аргументу х дает плотность вероятности рг (у), а по аргументу у — плотность вероятности р,(х).

ПРИМЕР 1. Задано распределение вероятностей дискретной двумерной случайной величины:

Требуется: а) найти законы распределения составляющих X и Y;

Ь) составить функцию распределения.

РЕШЕНИЕ:

а) сложив вероятности «по столбцам», найдем закон распределения составляющей X:

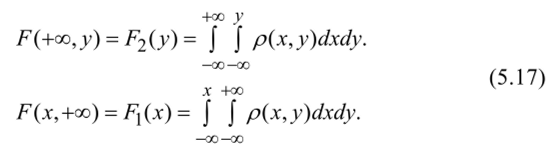
Сложив вероятности «по строкам», аналогично найдем закон распределения составляющей Y:

Ь) составим функцию распределения:

ПРИМЕР 2. (Задача Бюффона)

Иглу длиной / бросают на плоскость, на которой на расстоянии L друг от друга проведены параллельные линии. Определите вероятность пересечения иглой одной из линий, если / < L.

РЕШЕНИЕ. Введем систему случайных величин X, Ф, где X — расстояние от середины иглы до ближайшей линии, а <�р — острый угол между иглой и линией (см. рис.). Очевидно, что расстояние X распределено равномерно в интервале [О, L / 2], а угол ср распределен равномерно в интервале [0, л /2]. Учитывая, что СВ X и (р — независимые, получим f (x, (р) = 2/L? 2/л = А/kL при 0<�х</./2, 0 <(р < к/2. Пересечение иглой одной из линий происхо;

_Л /-sin® _.

дит при заданном угле (р, если 0 < х <-. Отсюда получим искомую вероятность: