Аффинные преобразования кольца вычетов

Пусть т е N, a, b е Z_m. Преобразование g кольца вычетов Z,", определяемое выражением g (x) — (ах + b)modm, называется аффинным (при 6 = 0 — линейным). При а Ф 0 такое преобразование называют линейным конгруэнтным генератором (ЛКГ), при этом константы а, Ь, т называются множителем, сдвигом и модулем соответственно.

Утверждение 7.2. Преобразование ЛКГ обратимо (а, т) = 1.

4 Рассмотрим линейное преобразование g (x) = ах modm. Преобразование g не обратимо, если не инъективно. Пусть ах = ay modm, где х> у, тогда а (х — у) = km, где 0 < х — у < т.и натуральное k < а. При (а, т) = 1 имеем противоречие, так как а не делит k.

Пусть (а, т) = d> 1. Тогда а / d, m / d е Z_m и g — не подстановка, так как g'(0) = 0 modm = (а / d) m modra = а (т / d) modm = g (m / d).

Преобразование ЛКГ обратимо обратимо g'(x), так как при любом с е Z_m уравнение (ах + b) mod/n = с разрешимо разрешимо уравнение ах mod/w = с — Ь. ?

Регистры сдвига

Функция у<�р: Xⁿ⁺ⁱ —" X(фу: Х^п+] —> X") называется функцией неавтономного регистра левого (правого) сдвига над кольцом X с обратной связью f (x, х"), где f (x_lt …, х"): X" —> X (часто X — поле), если она определяется системой, где у = x_n+i

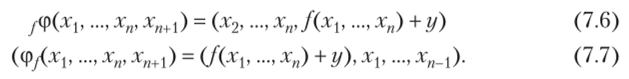
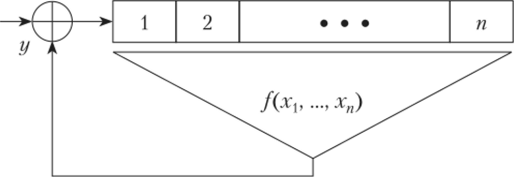
Рис. 7.1. Неавтономный регистр правого сдвига длины п.

На схемах регистр сдвига изображают в виде ряда из п ячеек памяти, в каждой из которых можно записать любой элемент множества X, и схемы, реализующей функцию f{x_x, х_п) (на рис. 7.1 стрелки указывают, что изображен регистр правого сдвига). Число п называют длиной регистра сдвига, f (x_x, …, х_п) — функцией обратной связи. Переменные x_lf …, х_п называют внутренними, переменную у — входной. Вместо операции + (сложения в кольце X) можно использовать другую операцию т (обычно т биективна по обеим переменным).

Преобразование^* (gy) множества X^й называют преобразованием автономного регистра левого (правого) сдвига над X с функцией обратной связи f (x 1 х_п):

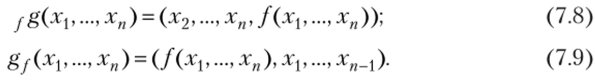
Отображение (преобразование) регистра сдвига над кольцом X является линейным, если линейна функция обратной связи. Соответствующие регистры называются линейными регистрами сдвига (ЛРС) над кольцом X.

Теорема 7.5. Преобразование jg регистра левого (правого) сдвига множества Х^п биективно f (x_u …, х_п) биективна по переменной х_х (по х_п).

Л Пусть преобразование jg регистра левого сдвига небиективно. Тогда в множестве Х^п найдутся два набора: р = (р, р₂, р") и v = (v_v v₂, v"),.

p Ф v, такие, что yg'(p) = /g'(v). Отсюда и из равенства (7.8) имеем (р₂, …, Р_w,/(Pj, Ц₂> •••> Ни)) = (^v2> •••> ^vtrf (^vv ^v2' ^vn)y Поскольку p Ф v, то отсюда имеем, что р, Ф v_t, и в то же время /(p_t, р₂, …, р") = /(v_1? v₂,…, v"). Значит, подфункция f (x, р₂, р") — не подстановка множества X.

Обратно, если jg — подстановка, TOyg*(p) Ф /g (v) при различных р, v е Х^п, в частности при р = (р_1? р₂, …, р"), v = (v" р₂, …, р_я), где p_t Ф v_t. Тогда, используя (7.8), получаем (р₂, р₃,x_n, f (p_x, р₂,…, pj) Ф (р₂, р₃, р_wf (y_v р₂, …, р")). Значит,/(pj, р₂, …, р") Ф /(Vj, р₂, …, р"). В силу произвольности выбора элементов pj, р₂, …, р", (лишь бы p_t Ф v_{) отсюда следует, что для любых р₂,…, р" е X подфункция f (x, р₂,…, р") есть инъективное и, значит, биективное преобразование X. ?

Следствие. Преобразование jg (gy) регистра левого (правого) сдвига над CF (2) с обратной связью f (x_x, …, х_п) биективно f (x…, х_п) линейна по переменной х_х (по х_п)

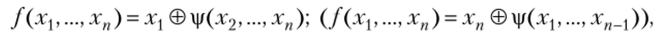
где р — произвольная б.ф. от п — 1 переменной.

Ч Булева функция / от переменной х есть подстановка множества {О, 1} «либо / = х © 1, либо / = х. Если б.ф. /(xj, …, х_п) линейна по х_1у то при любой фиксации переменных х₂, х_п она равна либо х_1у либо х_{® 1, т. е. является подстановкой множества {0, 1}. Тогда по теореме 7.5 регистр сдвига с обратной связью f (x_v …, х_п) реализует подстановку множества V_n.

Обратно, пусть /(х_1? х_п) не линейна по переменной х_{, тогда ее разложение по первой переменной есть f (x_{,…, х_п) = х{^_х{х₂, х_п) © |/₀(х₂, •••> х_п), где f (x₂,…, х_п) отлична от константы 1. Если |/i (a₂, a") = 0, то /(х,.

a₂, CL_n) = |/₀(ос₂, a") = const, т. е./(х, a₂,…, a") — не подстановка мно жества {0, 1}. По теореме 7.5 регистр сдвига с обратной связью /(х_1? …, х_п) реализует небиективное преобразование множества V_n. ?

Между множествами регистров левого и правого сдвига имеется очевидная биекция. Далее рассматриваются, если не оговорено противное, регистры левого сдвига над кольцом X.

Обозначим через jg_a преобразование множества Х^п, реализуемое неавтономным регистром сдвига с обратной связью /(х_1? …, х_п) при входном символе у = а (равенство (7.6)), а е X, и через jS — систему преобразований: j-S = {jg_a а е X}. Система j-S нелинейного (аффинного) регистра над нолем состоит только из нелинейных (аффинных) преобразований.

Полугруппой неавтономного регистра сдвига с обратной связью f (x_u …, х_п) называется полугруппа (обозначим ее jG)_y порожденная системой j-S, т. е. fG = (jg_a: а е X). Если /(х_1? …, х_п) биективна по х_х, то jg_a — подстановка множества Х^п при любом а е X (теорема 7.5), тогда jG — группа. Полугруппой (группой) автономного регистра сдвига с обратной связью f (x_v …, х_п) называется циклическая полугруппа (группа) _fG = (jg), где преобразование (подстановка) jg определено равенством (7.8).

Некоторые свойства полугрупп и групп регистров сдвига даны в [10].

Пусть^-Г — помеченный граф полугруппы (группы) jG неавтономного регистра сдвига с обратной связью f (x_{, …, х_п), построенный, но системе образующих fS. Множество вершин графа уГ есть Х^п, множество меток дуг графа есть X Тройка (х, а, у) е Х^п х X х X^й есть помеченная дуга графа уГ При различных функциях f (x_t, …, х_п) графы jT совпадают с точностью до меток. Непомеченный граф у Г двоичного регистра сдвига длины п называют графом де Брёйна порядка п.

Утверждение 7.3. В графе уГ регистра сдвига длины п

• а) не имеется кратных дуг;
• б) любая вершина «-достижима из любой вершины;
• в) полустепени захода и исхода всех вершин равны |х|.

М а) в силу (7.6) наличие кратных дуг в графе уГ равносильно совпадению векторов:

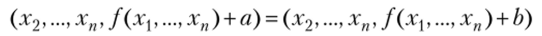
при а Ф b, a, b е X. Имеем противоречие по последней координате, т. е. в уГ нет кратных дуг;

б) в уГ вершина (у_{,…, у_п) «-достижима из вершины (х_{у…, х_п)_у так как из (7.6) следует:

• 1) дуга ((х" х_п), (х₂,…, х_п, г/,)) имеет метку а_х = г/, -f (x_x,…, х_и);
• 2) дуга ((х₂,… х", г/]), (х₃,х_п, у_х, у₂)) имеет метку а₂ = у₂ -/(х₂,…, х",

УУ ;

п) дуга ((х", г/,у"_{)), (у_х,…, у,)) имеет метку а" = у_п ~/(х", у_х у"__х).

Таким образом, указан путь длины п в уГ из (х_ь …, х_п) в (у_х,…, у");

в) дуга ((xj, …, х_и), (х₂, …, х_п, у)) при любом у е X имеет метку /(х_х,…, х") + у. Дуга ((у, X],…, х_п__х), (х,…, х")) при любом у е X имеет метку f (y, х,…, х"__х) + х". Тогда полустепени исхода и захода любой вершины графа / равны |Х|. ?

Следствие. Группа jG биективного регистра сдвига транзитивная.

Ч По утверждению 7.36 граф /Г сильно связный, значит, группа jG транзитивная. ?