Определение видимости. 
Компьютерная графика

Очень часто в компьютерной графике возникают задачи, связанные с проектированием различных объектов на плоскость. Далее будем считать, что используется перспективное проектирование с заданным центром с (весь материал этого параграфа легко переносится и на случай параллельного проектирования). При таком проектировании одни объекты могут закрывать собой (полностью или частично) другие объекты от наблюдателя, расположенного в точке с. Поэтому для построения корректного изображения мы должны не просто спроектировать объекты на плоскость (часто называемую картинной плоскостью), но и определить, какие объекты или части объектов будут видны на этой плоскости (а какие будут скрыты). Соответствующая задача называется задачей определения видимых поверхностей, в англоязычной литературе обычно используется термин HSR (Hidden Surface Removal).

Несмотря на то что данная задача на первый взгляд кажется довольно простой, в действительности эго не так. Более того, для современных задач, возникающих в компьютерной графике, необходимо определять видимость для очень большого набора сложных объектов. При этом в любой момент времени обычно видна лишь очень малая часть от общего числа объектов. Поэтому если мы хотим не просто получить корректное изображение, но и сделать это достаточно быстро, то задача определения видимости становится очень важной. Можно показать, что эта задача имеет очень много общего с сортировкой. Фактически каждый алгоритм определения видимости содержит в себе сортировку в той или иной форме.

Далее будем считать, что все объекты, которые мы хотим изобразить, представлены в виде наборов непрозрачных треугольников. Для того чтобы определить видимость, постоянно придется сравнивать различные объекты между собой. Соответственно, алгоритмы определения видимости можно разделить на два класса в зависимости от того, где именно производится сравнение объектов. С одной стороны, можно сравнивать объекты между собой непосредственно в исходном трехмерном пространстве; с другой стороны, — сравнивать не сами объекты, а их проекции на картинную плоскость. Также мы можем разделять алгоритмы еще по точности получаемого результата. Можно производить точное сравнение объекта и получить результат в виде набора многоугольников на картинной плоскости, вообще никак не привязываясь к растровой решетке.

В то же время задачи определения видимости решают и в дискретном случае — для набора пикселов на картинной плоскости. Получаемое в данном случае решение привязано к разрешению растровой решетки. При смене разрешения необходимо решать задачу заново.

Рассмотрим несколько важных понятий, связанных с определением видимости. Первым из них является понятие лицевой (и нелицевой) грани. Пусть у нас есть замкнутый многогранник. Тогда для каждой его грани мы можем задать единичный вектор внешней нормали. Рассмотрим, в какую сторону направлен этот вектор. В случае, когда он направлен к центру проектирования (наблюдателю), будем называть эту грань лицевой, в противном случае — нелицевой (рис. 7.7).

Иными словами, для того чтобы определить, является ли заданная грань лицевой или нет, мы строим вектор v от какой-либо точки этой грани к центру проектирования с и смотрим на знак скалярного произведения (v, п). Если это скалярное произведение больше нуля, то грань лицевая, в противном случае — нелицевая.

Может показаться, что результат этой проверки зависит от выбора точки на грани, из которой мы строим вектор v. Однако на самом деле это не так: знак скалярного произведения зависит только от того, в каком полупространстве относительно плоскости, проходящей через грань, лежит центр проектирования с. Грань лицевая, если центр проектирования лежит в том же полупространстве, в которое направлена внешняя нормаль к грани.

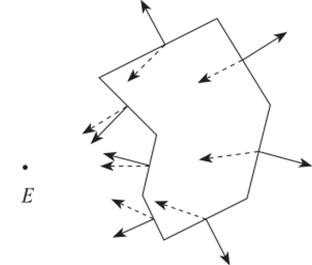
Рис. 7.7. Лицевые и нелицевые грани.

Считая грани непрозрачными, мы никогда не сможем увидеть ни одну из нелицевых граней. Таким образом, нелицевые грани можно сразу же отбросить и рассматривать только лицевые, что позволяет снизить число рассматриваемых граней примерно вдвое.

Еще одним важным понятием является сложность по глубине (depth complexity). Его сначала вводят для произвольной точки на картинной плоскости, а потом находят среднее значение сложности по всем точкам. Для того чтобы определить эту сложность, проведем луч из центра проектирования через соответствующую точку на картинной плоскости. Этот луч может пересечь некоторые из граней сцены. Тогда сложностью по глубине для данной точки называется число пересечений луча с лицевыми гранями (рис. 7.8).

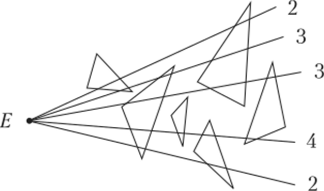
Рис. 7.8. Сложность по глубине для набора точек.

При построении изображения у нас есть заданная растровая сетка с конечным числом пикселов. Для каждого из них мы можем найти сложность, но глубине и затем усреднить полученные значения. Эта средняя сложность по глубине определяет сложность задачи определения видимости для данной сцены и заданного проектирования. Чем эта сложность выше, тем сложнее решить задачу определения видимости. Для многих сцен, встречающихся в современных приложениях, например 31)-шутерах, эта сложность оказывается очень велика: мы видим лишь очень малую долю от общего числа граней.

Соответственно, многие современные методы определения видимости используют специальные алгоритмы, позволяющие быстро отбросить основную часть невидимых граней без их явного перебора. После этого для определения видимости среди оставшихся граней используется какой-либо другой метод, например рассматриваемый далее метод буфера глубины.

Еще одним важным понятием является понятие загораживателя {occluder). Любой объект сцены определяет некоторую область пространства, которая гарантированно не видна при данном проектировании (рис. 7.9).

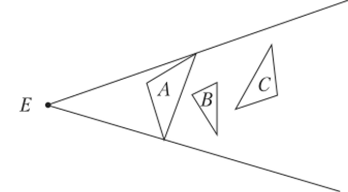
Рис. 7.9. Случай, когда объект А выступает в роли загораживателя и скрывает объекты В и С.

Таким образом, любой объект, целиком попавший в эту область, может быть сразу же отброшен как заведомо невидимый. Если у нас есть несколько загораживающих объектов, то вместе они позволят отбросить гораздо больше объектов, чем при рассмотрении каждого из них по отдельности (рис. 7.10).

Рис. 7.10. Случай, когда ни один из объектов А и В, взятый по отдельности, не поможет отбросить объект С.

Еще одним важным понятием в задаче определения видимости является когерентность (coherence). Именно эффективное использование когерентности позволяет строить эффективные методы определения видимости. Выделяют следующие типы когерентности:

• • между объектами;
• • между гранями;
• • между ребрами;
• • между пикселами;
• • между кадрами.

Когерентность между объектами означает, что два находящихся рядом объекта, скорее всего, или одновременно видны, или одновременно не видны. Аналогично, когерентность между гранями означает, что если одна грань объекта видна, то и соседняя с ней грань этого же объекта, скорее всего, также видна.

Когерентность между ребрами означает, что расположенные рядом ребра, вероятно, одновременно видны. Когерентность между пикселами означает, что если данный пиксел соответствует какой-то грани, то и соседние с ним пикселы также соответствуют той же грани. Когерентность между кадрами означает, что множество видимых граней почти не меняется от кадра к кадру.

Однако когерентность вовсе не означает, что эти свойства всегда выполняются. Они, скорее, отражают общие тенденции и подход к оптимизации алгоритмов определения видимости.