Конечные поля. 
Криптографические методы защиты информации. 
Часть 1. Математические аспекты

Поле, состоящее из конечного числа элементов, называется конечным.

Определим строение полей. Если Р, Р — поля и F cz Р, то F называется подполем поля Р, а Р называют надполем или расширением поля F. Поле, не содержащее других нетривиальных подполей, называется простым полем.

Конечный порядок единицы ноля Р как элемента аддитивной группы поля Р называется характеристикой поля Р. Иначе характеристика поля полагается равной 0. В частности, ноля Q и R имеют характеристику 0. Если характеристика поля равна 0, то простое подполе изоморфно полю Q. Каждое поле есть расширение своего простого подполя.

По следствию 1 из теоремы 2.11 характеристика поля есть простое числор. Подполе характеристики р (обозначается GF (p) или F_/;), порожденное единицей, совпадает с Z_f) и является простым полем. Отсюда каждое конечное поле характеристики р содержит простое подполе GF (ji).

Если Р с Р, то поле F можно рассматривать как векторное пространство над полем Р, размерность которого называется степенью расширения поля Р с Р, обозначается [Р: Р].

Элемент а е Р называется алгебраическим над полем Р, если а есть корень ненулевого многочлена f (x) е Р[х], при этом многочлен/(х) называется аннулирующим многочленом элемента а. Нулевой многочлен считается аннулирующим для любого элемента поля.

Минимальным многочленом элемента а (обозначается гп_а(х)) называется его аннулирующий унитарный многочлен наименьшей степени. Множество всех аннулирующих многочленов элемента а обозначим Р_а[х.

Теорема 4.12. Для любого элемента а, алгебраического над Р.

• а) Р_а[х] — идеал кольца Р[х]
• б) т_а{х) определен однозначно, неприводим и m_a(x)f (x) для любого /(х) € Р_а[х].

М а) множество Р_а[х] замкнуто относительно сложения, так как если многочлены f (x)_y …_yf_r(x) е Р_а[х, то любая их линейная комбинация также аннулирует а. Если/(х) е Р_а[х, то и f (x)g (x) е Р_а[х] для любого g (x) е Р[х. Следовательно, Р_а[х — идеал;

б) пусть т_а(х) и х_а(х) — различные минимальные многочлены элемента а, тогда ненулевой многочлен ш_а{х) — х_а(х) е Р_а[х] и имеет в силу унитарности многочленов т_а(х) и р"(Х) степень меньше, чем degт_а(х). Имеем противоречие с минимальностью многочлена т_а(х).

Если т_а(х) разлагается в произведение многочленов ненулевой степени, т_а(х) = т_{(х)т₂(х)_у то из т_а(а) = 0 следует, что один из многочленов т₁(х)_у т₂(х) аннулирует элемент а. Поскольку degт?х) < degт_а(х)_у i = 1, 2, то имеем противоречие с минимальностью т_а(х).

Пусть т_а(х) не делит некоторый /(х) из Р_а[х, тогда разделим f (x) на т_а(рс):

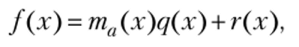
где degr (x) < degт_а(х) и по теореме 4.12а г (х) е Р_а[х_у что противоречит минимальности т_а(х). ?

Теорема 4.13. Всякое расширение Р с F конечной степени является алгебраическим, т. е. все элементы поля Р — алгебраические над полем F.

Ч Пусть А = {1, а, …, а^п)_у где а е F_y п = [F: Р]. Поскольку | А > п, то элементы множества А линейно зависимы, т. е. найдутся элементы с₀, c_v …, с_п е Р такие, что с₀ + с_{а + … + с_па^п = 0. Таким образом, найден аннулирующий многочлен элемента а. ?

Опишем Р (а) — наименьшее подполе поля F, содержащее элемент а и поле Р. Если элемент а алгебраический над Р, то подстановка а вместо х порождает эпиморфизм колец Р[х —> Р[а_у ядро которого по теореме 4.12 есть идеал т_а(х)Р[х. Иначе, Р[а] — это фактор-кольцо кольца многочленов Р[х] по модулю минимального многочлена т_а(х). Поскольку т_а(х) неприводим, то по следствию теоремы 2.20 поле Р (а) = Р[а].

Элемент а называется примитивным элементом расширения поля Р с с Р (а)_у это расширение называют простым алгебраическим расширением, степень его равна degт_а(х). Конечное расширение F поля Р называется полем разложения неприводимого над Р многочлена f (x)_y если F — наименьшее иоле, порожденное нолем Р и корнями многочлена f (x). По теореме Безу многочлен f (x) разлагается на линейные множители из кольца многочленов F[x],

Любое конечное поле Р содержит простое подполе F_/;, пусть степень расширения Р: F_/;] равна п и х_{у х_п — базис расширения. Тогда любой элемент х е Р однозначно представим в виде х = с_{х_{ + … + с_Г1х_пУ где с_{у …, с_п е F._r Заметим, что рх = 0 для любого хе Р. Каждый коэффициент может принятьр значений, поэтому | Р = р^п. Покажем существование поля Галуа GF (pⁿ) порядка р^п для простого р и любого натурального п.

Лемма 4.1. Многочлен уц (х) = хР^п-х не имеет кратных корней в поле разложения характеристики р.

Ч Производная многочлена |/(х) имеет вид f'(x) = р^пх^рП~^х -1 = -1. Значит, |/(х) — взаимно простой с и по теореме 2.16 |/(х) не имеет кратных корней в поле разложения. ?

Теорема 4.14. Поле разложения многочлена |/(д) содержит р^п элементов.

Ч Достаточно показать, что все р^п корней многочлена образуют поле. Пусть а, b — ненулевые корни многочлена |/(х), а значит, и многочлена _хр^п-1−1. Тогда (ab)Pⁿ~^{ = аР^п~^{Ь^рП~^х =1. Учитывая, что формуле бинома Ньютона все слагаемые кроме первого и последнего кратны степени, имеем (а + Ь) Р^п =а^рП +Ьр^п = a + b. ?

Следствие. Все поля Галуа GF (pⁿ) изоморфны.

Теорема 4.15. В конечном поле Р мультипликативная группа Р* является циклической.

4 Группа Р* имеет порядок р^п — 1 и является абелевой. Если Р* не циклическая, то в соответствии с теоремой 4.8 ПОК порядков всех ее элементов равен собственному делителю г числа р^п — 1. Следовательно, (я,)' = 1 для любого cij е Р*. Отсюда многочлен х^г — 1 аннулирует любой элемент группы Р*, значит х^г — 1 делится на минимальный для всех элементов группы Р* многочлен П (^х ~ ^а)• Имеем противоречие, так как.

«={1…р^п-1}.

deg П (х-а_{)>г. ?

Образующий элемент а циклической группы GF*(pⁿ) называется примитивным элементом поля GF (pⁿ). Если взять элемент а в качестве примитивного элемента расширения F_/; с GF (pⁿ)> то получаем, что всякое конечное поле характеристики р является простым алгебраическим расширением поля F_/;, так как оно порождено элементом а. Следовательно, минимальный многочлен т_а(х) примитивного элемента а поля GF (pⁿ) имеет степень п, и поле GF (pⁿ) изоморфно факторкольцу F_f)[x] / m_a(x)_f где многочлен т_а(х) неприводимый, degт_а(х) = п и т_а(х)хР^п~¹ — 1.

Теорема 4.16. GF (pⁿ) есть поле разложения всякого неприводимого многочлена f (x) степени п над полем ?_р.

4 Если а — корень неприводимого многочлена/(х), то IF_/;(c/): ?_р] = п. Поэтому F_р(а) = GF (pⁿ). Используя бином Ньютона для поля характеристики р, имеем f (aP) = f (a)P. Следовательно, элементы а, аР_у …, а^рП~¹ есть корни многочлена f (x). Докажем, что эти корни различны.

Пусть корни не различны, иa^pJ = а^р, где 0 1. Возведя равенство в степень р^п~^к_у получим a^ptl~^k+j — а. Тогда неприводимый многочлен /(.г) делит аннулирующий многочлен х^{р, 1}~^к+) +х. Отсюда F_р(а) — подполе поля GF (p^Tl~^k+j), где п — k + j < п. Имеем противоречие. ?

Следствие. Порядки всех корней многочлена f (x) в группе GF (pⁿ) равны.

4 ordа | р^п — 1, тогда ordfl^ = ordа / (p^k_f ordа)_у где (р^к, ordа) = 1, к = О, …, п — 1. ?

Назовем порядком многочлена f (x) е F_;,[x], где /(0) Ф 0, наименьшее натуральное число t, при котором f (x) од — 1 (обозначается ordf (x)).

Теорема 4.17. Если /(х) — неприводимый многочлен степени п над нолем F_/;, то ord/(x) совпадает с порядком любого его корня в мультипликативной группе поля разложения.

4 Пусть /(а) = 0, тогда orda = t, где t р^п — 1. Значит, а — корень многочлена X^е- 1 и по теореме Безу (х — а) | х* - 1. По следствию из теоремы 4.16 порядки всех корней многочлена /(х) равны, тогда из разложения /(х) на линейные многочлены получаем /(х) x^t — 1. ?

Теорема 4.18. Поле GF (pⁿ) содержит подполе GF (ji^d) для любого d .

4 Любому элементу а (не обязательно примитивному) поля GF (pⁿ) соответствует минимальный неприводимый унитарный многочлен т_а(х). Пусть degm"(x) = d, тогда F_р(а) — расширение степени d поля F_y, и | F_р(а) I = p^d. Вместе с тем, GF (pⁿ) — расширение степени г поля F_;,(tf) ир^п — I GF (pⁿ)| = p^dr. Отсюда d .

Обратно, для любого d поле GF (p^d) содержится в поле GF (pⁿ), так как любое решение уравнения x?^d -х есть решение уравнения хр^п -х. ?

Теорема 4.19. Многочлен хР^п -х, п — натуральное, разлагается в F_/;[x] в произведение всех унитарных неприводимых многочленов всех степеней d .

4 Если а — корень неприводимого унитарного многочлена /(х) степени d над полем F_/;, то F_p(a) — подполе поля GF (pⁿ). Поскольку а — корень многочлена хР^п -х, то/(х)хР^п -х.

Обратно, пусть /(х) — неприводимый унитарный многочлен, делящий хР^п -х. Тогда все его корни принадлежат GF (pⁿ). Отсюда degf (x) в соответствии с теоремой 4.18, так как присоединение корня /(х) к F_/; дает подполе в GF (j)ⁿ). Следовательно, неприводимые унитарные многочлены, делящие х^рп -х, имеют степень d, где d . По лемме 4.1 хР^п -х не имеет кратных корней. Значит, х^рП -х есть произведение всех таких многочленов. ?

Следствие. Если п — простое число, то в F_/;[x] имеется (р^п -р) / п неприводимых унитарных многочленов степени п.

4 Число (р^п — р) / п — целое при простом и, так как р^п = p (mod^) по малой теореме Ферма. Пусть и (п) — число неприводимых унитарных многочленов степени п. По теореме 4.19 многочлен хР^п -х степени р^{, г} есть произведение и (п) многочленов степени пир неприводимых многочленов х — а степени 1, где а е F_/r Приравнивая показатели степеней, получаем р^п= пи (п) + р. Отсюда следует формула для и{п). ?

Пусть п — не обязательно простое число, обозначим u{d) — число неприводимых над F_;, унитарных многочленов степени d. Тогда получаем соотношение.

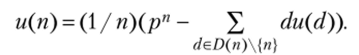
Теорема 4.20. Умножение (деление) элементов ноля GF (pⁿ) требует O (nog^sp) двоичных операций, возведение в степень к е N не более 0(nogkog³p) двоичных операций.

М Пусть f (x) — неприводимый унитарный многочлен степени п над F^, тогда элемент поля GF (p^rl) есть многочлен из F_p[x], взятый по модулю f (x).

Перемножение двух элементов требует порядка п¹ умножений коэффициентов мономов (сложение коэффициентов менее трудоемко). Деление на f (x) требует порядка О (п) делений целых чисел по модулю р и 0(п²) умножений целых чисел по модулю р. Умножение целых чисел по модулю р требует порядка 0(og²p) операций, а деление целых чисел по модулю р с использованием, например, алгоритма Евклида требует по следствию 1 из теоремы 2.7 порядка 0(og³p) операций. Тогда общее число операций равно 0(n²og²p + nog³p), что не больше O (nog³p) двоичных операций.

Чтобы получить такую же оценку для деления, покажем, что обратный элемент можно найти за 0(nog³p) операций. Используя алгоритма Евклида для многочленов над F_/;, требуется записать 1 как линейную комбинацию f (x) и элемента поля, т. е. многочлена степени меньше п. Это включает 0(п) делений многочленов степени меньше п, а каждое деление требует 0{n²og²p + nog³p). Тогда общее время не выше 0(nog³p) двоичных операций.

Возведение в степень методом повторного возведения в квадрат потребует O (logA) умножений и всего 0(nogkog³p) двоичных операций. ?