Общее равновесие в производстве

Проанализируем теперь другую сторону экономики — производство. Пусть в экономике производится два товара (X и Y). В производственном процессе задействовано два вида ресурсов — труд L и капитал К. Общий объем трудовых ресурсов составляет L; общий объем капитальных ресурсов равен К. В производстве товара X задействовано L_x труда и К_х капитала. В производстве товара Y занято L_y труда и К_у капитала, так что.

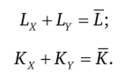
Рассмотрим экономику конкурентных рынков. Цены товаров и цены ресурсов заданы равновесными состояниями соответствующих рынков. Фирмы не могут оказать влияние на цены, фирмы являются ценополучателями. Цель фирм заключается в максимизации прибыли при технологическом ограничении, заданном производственной функцией. Цель потребителей — максимизация полезности от покупок товарных наборов. Производственные функции и функции полезности представлены стандартными моделями.

Используем для анализа диаграмму Эджуорта (рис. 21.7). По горизонтальной оси будем откладывать объемы применяемого труда, по вертикальной — объемы капитальных ресурсов. Факторы производства для выпуска товарах изображены в стандартном представлении: изокванты возрастают слева направо. Факторы производства для выпуска товара Y даются в перевернутом виде: изокванты возрастают справа налево.

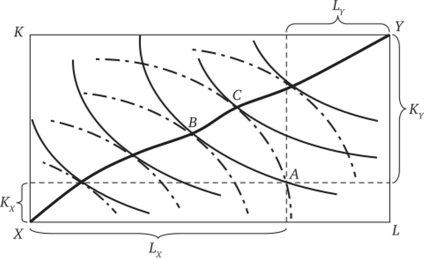
Рис. 21.7. Диаграмма Эджуорта для общего равновесия в производстве.

Пусть первоначальное распределение ресурсов в экономике представлено точкой А. В этой точке две изокванты двух производственных процессов пересекаются. Является ли эта точка оптимальной с точки зрения общего равновесия? Согласно критерию Парето точка А не является точкой эффективного распределения производственных ресурсов в экономике между выпусками товаров X и У. Путем перераспределения факторов производства, например в точку В или точку С, можно увеличить совокупный выпуск хотя бы одного из товаров, не сокращая производство другого изделия. Так как точки, А и В расположены на одной и той же изокванте для товара X, то переход из точки А в точку В увеличит выпуск товара Y без уменьшения производства товара X. Поскольку точки, А и С расположены на одной и той же изокванте для товара У, то переход из точки, А в точку С увеличит выпуск товара X, не сокращая объема производства товара У. Перераспределение ресурсов вдоль линии ВС будет способствовать росту выпуска и одного, и другого товара.

Как найти точки В и С и аналогичные им?

Возьмем две репрезентативные фирмы, одна из который занимается выпуском только товара X, а другая производит только товар У. Каждая фирма стремится нанять ресурсы в таком соотношении, чтобы максимизировать свою прибыль. Так как речь идет о конкурентной экономике и фирмы не могут оказывать влияние на ценовые параметры производства, то задача максимизации прибыли сводится к задаче максимизации выпуска:

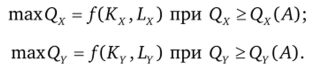
Решая эту задачу, получаем результат: MTRS*, = MTRS^Y_Kl. Эффективность общего равновесия в производстве наблюдается там, где изокванты соответствующих выпусков касаются друг друга, так что предельные нормы технологического замещения ресурсов в производстве разных товаров равны между собой. Эти точки формируют кривую производственных контрактов (утолщенная линия ХУ на рис. 21.7). Кривая производственных контрактов показывает альтернативные комбинации ресурсов и альтернативные комбинации товаров, которые могут быть произведены при эффективном использовании факторов производства.

Поскольку общий объем каждого ресурса в экономике фиксирован в каждый данный момент, то кривая производственных контрактов одновременно показывает границу производственных возможностей этой экономики. Выразив кривую производственных контрактов в виде функции: Q_x = f (Q_Y), получим кривую производственных возможностей (рис. 21.8), хорошо известную нам по гл. 2.

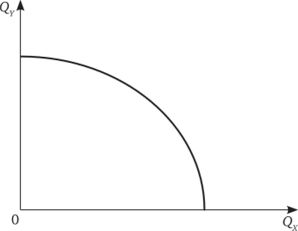
Рис. 21.8. Кривая производственных возможностей экономики.

Теперь можно проанализировать детально наклон КПВ. Наклон кривой производственных возможностей показывает предельную норму продуктовой трансформации — пропорцию, в которой выпуск одного товара (скажем, товара X) может быть заменен производством другого товара (товара У) с сохранением эффективности производства.

Предельная норма продуктовой трансформации (marginal rate of product transformation — MRPT) равна.

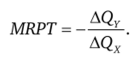
С другой стороны, кривая производственных возможностей может трактоваться как кривая затрат общества на выпуск двух товаров: С (Х; У). Эффективное производство требует полного использования имеющихся ресурсов, объем которых фиксирован. Поэтому вдоль КВП полный дифференциал функции затрат будет равен нулю:

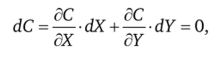
дС.

где — = МС_Х — предельные затраты общества на выпуск товара X;

ил.

дС

— = MC_Y — предельные затраты общества на выпуск товара Y; X и У — 8Y

объемы производства двух товаров.

ззо Перегруппировав слагаемые, получим еще одно выражение для предельной нормы продуктовой трансформации:

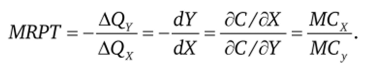
Таким образом, предельная норма продуктовой трансформации оценивает относительные издержки выпуска товаров, т. е. показывает альтернативные издержки производства.

Задача, иллюстрирующая концепцию Пусть в экономике используется один фактор производства — труд. Общий объем трудовых ресурсов составляет 100 чел.-ч. Экономика может производить товар X и товар У в соответствии с производственными функциями: X

и У=^-

Чему равна граница производственных возможностей экономики?

Чему равна предельная норма продуктовой трансформации в этой экономике?

Решение

Запишем общий объем труда в экономике: L_x+L_y =100. Подставим в это выражение значения ресурсов из соответствующих производственных функций:

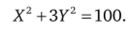
Это и есть функция КПВ данной экономики. Ее форма — эллипс при X > 0; У > 0. Найдем полный дифференциал данной функции.

Откуда получаем предельную норму продуктовой трансформации 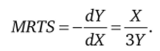Таким образом, альтернативные издержки выпускав составляют ЗУ.

Используя рассуждения, аналогичные ситуации, исследованной в денежной экономике обмена, можно доказать, что в денежной экономике производства равновесные цены ресурсов должны быть такими, чтобы:

MRTSu = MRTS^y_kl = Линия цен ресурсов в оптимуме будет касаться изоквант каждого вида производства. Если производственные функции представлены выпуклыми изоквантами (например, при стандартной модели в виде функции Кобба — Дугласа), то такая точка касания будет единственной для экономики с производством.