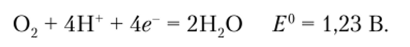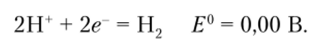Участие растворителя в окислительно-восстановительной реакции

В определенных случаях реагенты и продукты реакции могут вступать в окислительно-восстановительное взаимодействие с растворителем, в частности окислять или восстанавливать воду. Так, под действием достаточно сильного окислителя вода может быть окислена до кислорода в соответствии с полуреакцией.

Сильные восстановители, напротив, могут восстановить воду до водорода в соответствии с полуреакцией.

Оба эти потенциала уменьшаются с ростом pH, как показано на рис. 16.4.

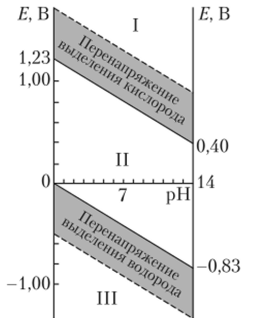
Рис. 16.4. Зависимость потенциалов окисления и восстания воды от pH.

Очевидно, что с точки зрения термодинамики все восстановители, имеющие потенциалы ниже потенциала восстановления воды, могут вытеснять водород из водных растворов. Практически из-за кинетических затруднений выделения молекулярного водорода граница восстановительной устойчивости воды на несколько десятых вольта меньше нуля. Эта дополнительная разность потенциалов, называемая перенапряжением выделения водорода, определяется механизмом реакции и зависит, в частности, от природы восстановителя и характера его поверхности. Например, перенапряжение выделения водорода на черненой платине, катализирующей этот процесс, равно нулю, а на ртутном электроде составляет около 0,8 В. На рис. 16.4 пунктирной линией показан средний эффективный потенциал выделения водорода с учетом перенапряжения в 0,5 В. Практически это означает, например, что большинство металлов реагирует с кислотами с выделением водорода, а наиболее активные — щелочные, щелочноземельные, лантаноиды и актиноиды — с водой и даже со щелочными растворами.

Средняя граница практической устойчивости окислителей в водных растворах (пунктирная линия на рис. 16.4) также превышает линию потенциала окисления воды примерно на 0,5 В — среднее значение перенапряжения выделения кислорода.

Таким образом, область между пунктирными линиями приближенно отражает диапазон устойчивости окислителей и восстановителей в водных растворах: окислители, имеющие более высокий потенциал, могут разлагать воду с выделением кислорода, а восстановители с более низким потенциалом — с выделением водорода. Отметим, что в отдельных случаях эти процессы идут довольно медленно, благодаря чему, например, при обычных условиях устойчивы в течении продолжительного времени водные растворы КМп0₄ [?⁰(МпО₄/Мп²⁺) =1,51 В] или солей церия (1У) [?°(Се⁴⁺/Се³⁺) = 1,61 В].