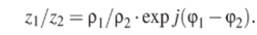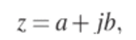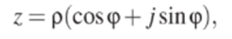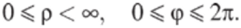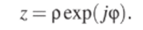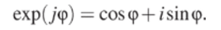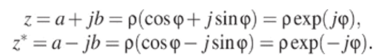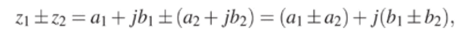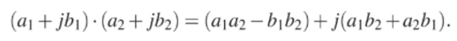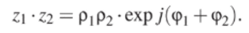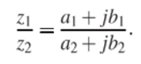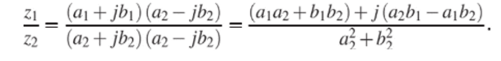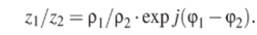Комплексные числа. 
Физика

Формально мнимой единицей j называют число, дающее в квадрате «минус единицу'': j2 = — 1.

Введение

мнимой единицы позволяет определить комплексные числа. Алгебраической формой комплексного числа называют выражение вида.

где а и b — произвольные действительные числа. Величину а называют реальной, а b — мнимой частью комплексного числа. Соответствующие обозначения имеют вид а = Re (z), b = lm (z). Частными случаями комплексного числа являются действительное число Im (z) = 0 и чисто мнимое число Re (z) = 0.

Комплексные числа наглядно изображаются векторами в комплексной плоскости, причем проекция этого вектора на ось абсцисс соответствует действительной части комплексного числа, а на ось ординат — мнимой. Комплексные числа равны, только если равны их и действительные, и мнимые части. Векгоры, изображающие равные комплексные числа, совпадают. Знак алгебраического неравенства в отношении комплексных чисел, вообще говоря, неприменим, и понятий «больше» — «меньше» для комплексных чисел не существует.

Тригонометрической формой записи комплексного числа называют выражение вида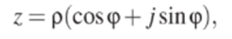

где р — модуль или абсолютная величина комплексного числа р = z = >/а*+7?, (р — его аргумент, ф = arctg (b/c*). Естественно, здесь.

Переход от алгебраической к тригонометрической форме представления комплексного числа эквивалентен переходу от декартовой к полярной системе координат в векторной алгебре.

Показательной формой представления комплексного числа называют выражение.

Для перехода от тригонометрической к показательной форме удобно использовать известную формулу Эйлера.

Два числа z и z* называют комплексно — сопряженными, если их действительные части (модули) одинаковы, а мнимые части (аргументы) отличаются только знаком:

Векторы, изображающие комплексно-сопряженные числа, расположены симметрично относительно действительной оси.

Сложение и вычитание комплексных чисел z и zi определяется формулой.

т.е. действия над действительной и мнимой частью производятся независимо.

Умножение комплексно — сопряженных чисел z и zi осуществляется по обычному правилу умножения многочленов.

Наиболее удобна при умножении показательная форма представления комплексного числа.

Наконец, деление комплексных чисел аналогично случаю действительных чисел определяется как действие, обратное умножению.

От «мнимости'' в знаменателе удобно избавиться, для чего числитель и знаменатель умножают на число z%₉ комплексно сопряженное делителю.

Таким образом, деление сводится к умножению делимого на число, комплексно сопряженное делителю, с последующим делением на квадрат его модуля (т.е. на действительное число). При использовании показательной формы все упрощается: