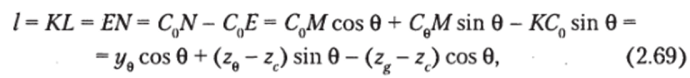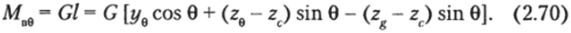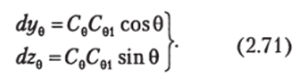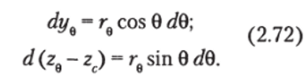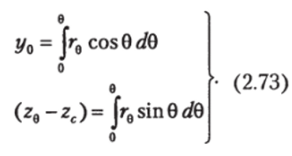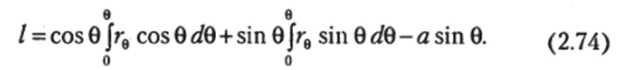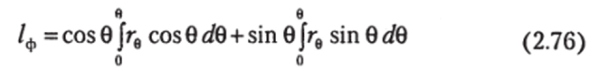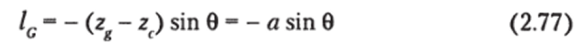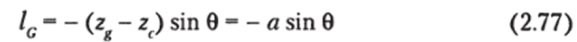Остойчивость на больших углах крена
В (2.69) и (2.70) фигурируют пока неопределенные координаты ЦВ в наклоненном положении. Для их нахождения приладим судну, накрененному на угол 0, дополнительное бесконечно малое наклонение dQ (рис. 2.12). Приращения координат ЦВ при этом запишутся. Где ус, zc — координаты ЦВ-точки С0 в первоначальном положении 0 — 0; yQ, ze — координаты ЦВ-точки С0 при наклонении судна на угол 0… Читать ещё >
Остойчивость на больших углах крена (реферат, курсовая, диплом, контрольная)
Полученные выше зависимости и выводы справедливы при малых углах наклонения. Для морских судов традиционной формы с достаточно большим отношением L/B > 5 дифферент в процессе эксплуатации не превышает обычно 3—4°, следовательно начальная остойчивость охватывает все реально возможные углы наклонения в продольной плоскости.
Иначе обстоит дело с поперечной остойчивостью: даже в условиях не очень суровой бортовой качки углы крена могут достигать 20°, известны случаи, когда они доходили до 50е и более. Поэтому возникает необходимость изучения наряду с начальной остойчивостью поведения судна при больших углах наклонения в поперечной плоскости. В этом случае заметно меняется площадь действующей ВЛ, соответственно претерпевают изменения момент инерции этой площади и метацентрический радиус [см. (2.8)]. Траектория центра величины перестает быть дугой окружности, метацентр меняет свое положение в процессе наклонения (рис. 2.10).
Линии действия сил тяжести судна G и поддержания yV перестают совпадать, возникает восстанавливающий момент. Чтобы найти плечо этого момента — плечо статической остойчивости — рассмотрим рис. 2.11, выполненный в более крупном масштабе. Очевидно, что искомое плечо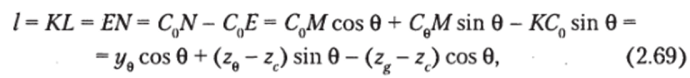 
где ус, zc — координаты ЦВ-точки С0 в первоначальном положении 0 — 0; yQ, ze — координаты ЦВ-точки С0 при наклонении судна на угол 0. Восстанавливающий момент — произведение силы на плечо
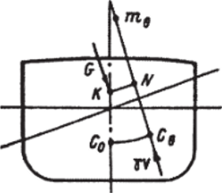
Рис. 2.10. Накренение на большой угол.
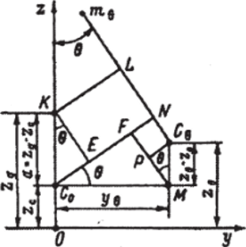
Рис. 2.11. К определению плеча статической остойчивости.
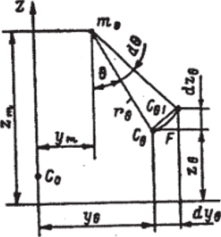
Рис. 2.12. К определению координат ЦВ накрененного судна.
В (2.69) и (2.70) фигурируют пока неопределенные координаты ЦВ в наклоненном положении. Для их нахождения приладим судну, накрененному на угол 0, дополнительное бесконечно малое наклонение dQ (рис. 2.12). Приращения координат ЦВ при этом запишутся
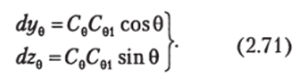
Учитывая, что при О, хорду можно заменить соответствующей дугой, т. е. С0С01, = гс/0, окончательно получим.
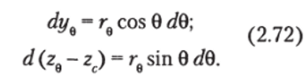
Проинтегрировав перемещения ЦВ за все время наклонения, найдем его координаты при угле крена 0:
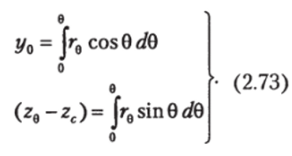
Тогда с учетом (2.69) для определения плеча статической остойчивости при больших углах наклонения будем иметь выражение.
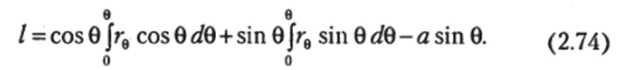
По аналогии с (2.20) запишем (2.74) в виде двух составляющих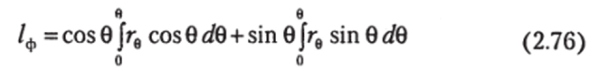 
где.
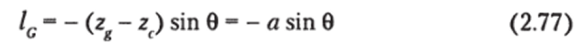
— плечо остойчивости формы и.
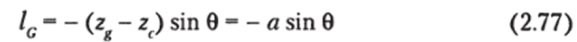
— плечо остойчивости веса, определяемое при заданном водоизмещении только положением ЦТ по высоте и углом крена.