Маятниковый маршрут с обратным холостым пробегом

На практике при планировании работы автомобилей по маятниковым маршрутам с обратным холостым пробегом руководствуются единственным правилом: последний пункт разгрузки автомобилей должен быть как можно ближе к автохозяйству. Считается, что при соблюдении этой основанной на здравом смысле рекомендации обеспечивается минимум пробега без груза. Анализ рассматриваемой задачи методом линейного программирования показал, что такое решение совсем неочевидно. Для доказательства рассмотрим пример.

Допустим, что с базы, А необходимо доставить продукцию потребителям Б1 и Б2. К ним автомобиль может сделать за время в наряде две ездки. Составьте маршрут движения автомобиля, дающий минимум порожнего пробега. Условия задачи, схема размещения потребителей, на примере решения которой составляется маршрут движения, приведены на рис. 11.14.

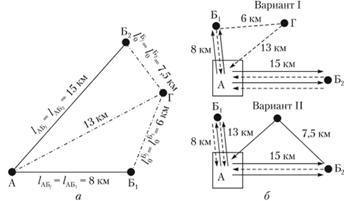
Рис. 11.14. Схема размещения потребителей (а) и варианты организации перевозок (б):

Г — автотранспортное предприятие; А — предприятие по поставке продукции; Б1, Б2 — потребители продукции; ГА — расстояние первого нулевого пробега; Б2Г, Б1Г — расстояние второго нулевого пробега При решении этой задачи могут возникнуть два варианта:

• 1) продукция поставляется в пункт Б2, а затем в Б1, из автомобиль поступает в АТП;
• 2) продукция поставляется в пункт Б1, а потом в Б2, автомобиль возвращается в АТП.

Для выбора варианта перевозки продукции произведем расчет коэффициента использования пробега автомобиля? и полученные значения сведем в табл. 11.3.

Таблица 11.3

Коэффициент использование пробега автомобиля

Как видно из таблицы, наиболее эффективен второй вариант, поскольку коэффициент использования пробега во втором случае выше, чем в первом.

Однако если руководствоваться правилом, что наименьший пробег достигается, когда первый пункт погрузки и последний пункт разгрузки находятся по близости от автотранспортного предприятия, целесообразен первый вариант (6 км < 7,5 км). Чтобы проверить правильность выбора, решим задачу математическим методом.

Задача составления рациональных маршрутов, обеспечивающих минимальный порожний пробст транспортных средств, сводится к следующей задаче линейного программирования:

минимизировать линейную формулу.

(11.11).

при условиях.

и 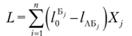(11.12).

Допустим, что пункты назначения занумерованы в порядке возрастания разностей :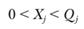

(11.13).

Тогда оптимальное решение таково:

(11.14).

где L — порожний пробег, км; 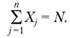 — расстояние от пункта Б, до автотранспортного предприятия (второй нулевой пробег), км; lАБ; - расстояние от, А до Бj (груженый пробег), км; j — номер (индекс потребителя; j = 1,2,…, п) Xj — количество автомобилей, работающих на маршрутах с последним пунктом разгрузки Бj; N — число автомобилей, работающих на всех маршрутах; Q, — объем перевозок (в ездках автомобиля).

Решая эту задачу, мы должны знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное число автомобилей заканчивает работу в пунктах назначения с минимальными разностями 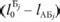, т. е. второго нулевого и груженого пробегов.

Для решения задачи необходимо исходные данные записать в специальную таблицу (матрицу), с помощью которой произвести все необходимые вычисления по составлению маршрутов (табл. 11.4).

Таблица 11.4

Исходные данные

Пункт назначения.	Количество груженых ездок.	Столбец разностей.

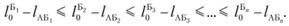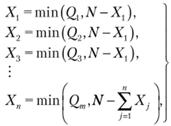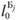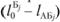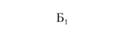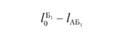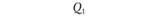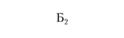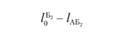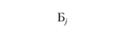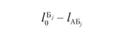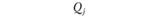Для каждого пункта назначения, т. е. по каждой строке, рассчитывают алгебраические разности 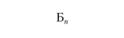, которые записывают в соответствующие клетки столбца разностей.

Рассмотрим применение предложенного алгоритма на примере, воспользовавшись исходными данными, приведенными на рис. 11.14.

Исходя из этих условий составляем таблицы объема перевозок (ездок) и расстояния перевозок (табл. 11.5 и 11.6).

Таблица 11.5

Объем перевозок (ездки)

Таблица 11.6

Расстояние перевозок, км

Таблица 11.7

Рабочая матрица условий

Наименьшую оценку (-7,5) имеет пункт Б2, в который необходимо сделать две ездки. Принимаем его последним пунктом маршрута А-Б2-Г, т. е. получаем маршрут варианта II (табл. 11.7).

Расчет экономической эффективности применения экономико-математических методов при маршрутизации перевозок определяют по формуле.

(11.15).

где Lгр — пробег автомобиля с грузом, км; ?1, ?2 — коэффициент используемого пробега, вычисленный до и после применения оптимизации; С1 — средние затраты на 1 км пробега автомобиля, коп.; З — расходы на выполнение расчетов по решению задач, руб.

После оптимизации маршрутов составляется сводная ведомость (табл. 11.8), в которой записано, сколько необходимо перевезти продукции потребителям, количество обслуживаемых автомобилей и время поступления автомобиля на склад и потребителю.

Таблица 11.8

Сводная маршрутная ведомость

№ маршрута.	Обозначение маршрута.	Расшифровка маршрута.				Показатели маршрута.
		АТП.	Склад.	Потребитель.	Склад.	Количество ездок.	Объем перевозок, т.	Количество автомобилей, ед.	Коэффициент использования пробега.
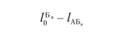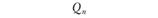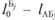	Г-А-Б.	Г.	А.	Б.	А …	nc.	Q	А,•.