Анализ временных рядов с учетом сезонной компоненты

О чем пойдет речь

• • Какие подходы к учету сезонной компоненты существуют при прогнозировании возможности ухудшения финансового положения?
• • Какие возможности открывает использование модели с аддитивной компонентой?
• • Какие особенности имеет модель с мультипликативной компонентой?

Какие подходы к учету сезонной компоненты существуют при прогнозировании возможности ухудшения финансового положения?

Мы познакомились с основными моделями, используемыми в прогнозировании. В некоторых простых случаях (для первичной оценки или относительной «прозрачности» будущего) их вполне достаточно для расчетов и планирования. Но более детальный анализ данных позволяет существенно повысить качество прогноза. Например, учет сезонной компоненты позволяет отличить сезонные колебания от изменений, которые могут свидетельствовать о неблагополучии и возможном развитии кризиса.

В качестве меры ответственности можно использовать ошибку прогноза — разницу между реальными данными и данными, полученными в результате расчетов. Обычно применяют среднее абсолютное отклонение (Mean Absolute Deviation, MAD):

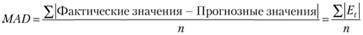(5.8).

и среднюю квадратичную ошибку (Mean Square Error, MSE):

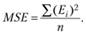(5.9).

Отметим, что MSE при наличии высоких ошибок резко возрастает.

Для моделирования временных рядов используются два типа моделей — аддитивная и мультипликативная. В каждой из них предполагается, что фактическое значение переменной А состоит из трендового значения Т, сезонной вариации S и ошибки Е. Как легко догадаться, в модели с аддитивной компонентой используется сложение отдельных компонент:

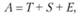(5.10).

а в модели с мультипликативной — их умножение:

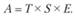(5.11).

Алгоритм проведения анализа одинаков в обеих моделях и состоит из четырех последовательных пунктов.

• 1. Расчет значений сезонной компоненты.
• 2. Десезонализация данных (вычитание сезонной компоненты из фактических значений) и построение тренда на их основе.
• 3. Расчет ошибок (разность между фактическими и трендовыми значениями, полученными на предыдущем этапе).
• 4. Расчет среднего абсолютного отклонения и среднеквадратичной ошибки (для проверки соответствия модели или выбора наилучшей).

На начальном этапе работы возникает естественный вопрос: чем же руководствоваться при выборе модели? Здесь важную роль играет динамика сезонных колебаний. Если со временем сезонная вариация остается достаточно ровной, это указывает на целесообразность выбора модели с аддитивной компонентой. Если же сезонная компонента не является константой, то лучше воспользоваться моделью с мультипликативной компонентой.

Какие возможности открывает использование модели с аддитивной компонентой?

Аддитивная модель прогнозирования может дать высокую точность результатов, если внутрисезонные колебания практически не меняются из года в год. Основными этапами ее использования являются:

• • нахождение центрированной скользящей средней, которую можно сравнивать с реальным значением за тот же период;
• • уменьшение значения ошибок и усреднение сезонной компоненты:
• • построение линейного прогноза на основе уравнения

x = at + b,

где t — номер периода (обычно квартала); х — десезонализированный тренд.

Для лучшего понимания рассмотрим конкретный пример.

Пример 5.5

В табл. 5.7 приведены данные о числе посетителей фитнес-центра «Самбо — Симба» по кварталам с января 2010 г. по июнь 2013 г.

Таблица 5.7

Количество посетителей фитнес-центра «Самбо — Симба» за 14 кварталов.

Отметим, что внутрисезонные колебания практически не меняются из года в год, что и позволяет выбрать для исследования аддитивную модель.

Чтобы исключить влияние сезонной компоненты, воспользуемся методом простого скользящего среднего. Просуммировав первые четыре значения, получим общий объем продаж за первый год, а поделив эту сумму на четыре — средний объем продаж в этом году. Причем это значение уже не содержит сезонной компоненты и соответствует середине первого года между 2 и 3 кварталами. «Скользя» но исходному ряду (повторяя эти вычисления и находя средние по 2−5 кварталу, 3−6 кварталу и т. д.), мы получим оценку искомого тренда.

Полученные таким образом значения тренда можно использовать для оценки сезонной компоненты. Нужно отметить, что для взвешенной оценки сезонной компоненты недостаточно только скользящих средних значений. Для первого года в нашем распоряжении их две: одна соответствует точке между 2 и 3 кварталами, вторая — между 3 и 4. Это связано с тем, что усредняя значения за четыре квартала, мы получаем число посетителей, соответствующее середине года. Однако нам необходимо получить десезонализированные оценки для квартальных значений, а не для промежуточных точек. Рассчитав среднюю из первой и второй оценки, мы получим среднюю на 3 квартал. Именно эту величину, называемую центрированной скользящей средней, мы и будем сравнивать с реальным значением за тот же период. С ее помощью проведем первичную оценку сезонной компоненты, воспользовавшись следующей формулой:

А — Т= S + Е. (5.12).

Результаты расчетов по которой приведены в табл. 5.8.

Таблица 5.8

Центрированная скользящая средняя и первичная оценка сезонной компоненты

Теперь для каждого квартала мы имеем оценку сезонной компоненты, включающую в себя ошибку. Для уменьшения значения ошибок и для усреднения сезонной компоненты проведем следующие преобразования: найдем средние значения для каждого сезона и скорректируем их таким образом, чтобы в сумме они давали ноль (этого легко добиться, прибавив к каждом}' их сумму, деленную на четыре, табл. 5.9).

Таблица 5.9

Расчет средних значений сезонной компоненты

Справочно: аналогичным образом определяется сезонная вариация за любой промежуток времени. Так, например, рассматривая вместо сезонов дни недели, уместно рассчитывать скользящую среднюю для семи дней. В этом случае значение тренда будет соответствовать середине недели, т. е. четвергу, и процедура центрирования не будет нужна. Объединим полученные результаты в табл. 5.10.

Таблица 5.10

Десезонализированные данные по компании «Самбо — Симба»

Здесь новые оценки значений тренда еще содержат ошибку, но на их основе с помощью метода проецирования тренда нетрудно построить линейный прогноз (x = at + b; в нашем случае t — номер квартала; х — десезонализированпый тренд (T + E)). Уравнение тренда имеет вид:

Т+Е= 1,93t+ 21,4.

Для расчета ошибок и прогнозирования по аддитивной модели построим таблицу, содержащую все итоговые компоненты (табл. 5.11).

Таблица 5.11

Итоговые данные

Последний столбец этой таблицы используем при расчете среднего абсолютного отклонения или средней квадратичной ошибки. В нашем случае MAD = 1,17; MSE = 1,68, что демонстрирует устойчивость и хорошее приближение при составлении краткосрочных прогнозов.

Сам прогноз по аддитивной модели рассчитывается следующим образом:

F=T+ S, (5.13).

где Т находим из уравнения линейного тренда, a S — это сезонная компонента, соответствующая прогнозируемому кварталу.