Количественные критерии эффективности

Из содержания параграфов 11.3 и 11.4 следует, что при количественной оценке эффективности инвестирования недостаточно ограничиться сравнением доходности портфеля 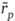с доходностью рынка 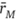. Обязателен также учет риска портфеля. Для этого были предложены различные показатели эффективности, явно учитывающие риск. Большинство из них действует в контексте модели САРМ.

Приведем наиболее распространенные показатели. Коэффициент Йенсена («апостериорная альфа»).

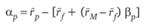
выражает отклонение по вертикали точки на плоскости (?, 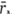), соответствующей реальному портфелю, от SML. Коэффициент Йенсена выражается в процентах (как и сама доходность г) и имеет смысл дополнительной доходности, которая получена сверх ожидаемой теоретически.

Коэффициент Трейнора

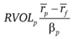
соотносит дополнительную (по сравнению с безрисковой) доходность портфеля с его рыночным риском.

Коэффициент Шарпа

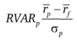
соотносит дополнительную доходность портфеля с его общим риском. Это наиболее важный и употребительный количественный показатель эффективности.

Пример 11.8

Средняя процентная ставка без риска равна 12% годовых, средняя доходность портфеля А составляет 16% годовых, портфеля В — 20% годовых. Стандартное отклонение доходностей портфелей А и В равны 3 и 7% соответственно. Используя формулу расчета коэффициента Шарпа, определим, при управлении каким портфелем будет достигнута большая эффективность:

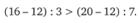
Ответ: А.

Поскольку различные коэффициенты предназначены для сравнения различных характеристик портфелей, может оказаться так, что из двух портфелей один является более предпочтительным по одному коэффициенту, но уступает по другому. «Точкой отсчета» .

для всех коэффициентов можно считать соответствующие характеристики рыночного портфеля:

¦ для коэффициента Йенсена — нулевой уровень;

¦ для коэффициента Трейнора — дополнительную доходность рынка ;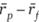

¦ для коэффициента Шарпа — величину .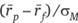

Метод V@R

Метод V@R («value at risk», «сумма под риском») — широко применяемый в риск-менеджменте метод оценки возможных убытков с заданным уровнем вероятности. Сама величина V@R с уровнем доверия р указывает на максимальный уровень потерь, который может быть достигнут с заданной вероятностью. Например, 95%-ная V@R 1 млн руб. означает, что с вероятностью 95% потери не превысят 1 млн руб. В «оставшихся» 5% случаев потери могу оказаться больше, чем 1 млн руб. (и даже значительно больше), однако такие исходы считаются крайне маловероятными, и ими пренебрегают.

Наиболее часто применяются два варианта метода — параметрический и исторический.

В параметрическом варианте метода V@R предполагается, что распределение доходностей портфеля является нормальным. Для расчета нужно знать параметры этого нормального распределения — математическое ожидание и стандартное отклонение (которое также называется волатильностью). Из смысла метода V@R следует, что требуется находить левые односторонние квантили нормального распределения.

Обычно используются следующие уровни доверия и соответствующие им односторонние квантили стандартного нормального распределения:

Если доходность портфеля имеет нормальное распределение с математическим ожиданием 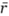и волатильностью (стандартным отклонением) ?, то р%-ная V@R портфеля равна.

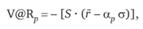
где S — стоимость портфеля в настоящий момент; ?р — р%-ная квантиль стандартного нормального распределения.

Знак «минус» перед выражением в правой части стоит потому, что V@R принято понимать как размер убытков.

Пример 11.9

Стоимость портфеля инвестора составляла 3 млн руб. Волатильность за месяц — 2,5%, ожидаемая доходность за месяц -1,5%. В портфель добавили безрисковый актив на сумму 2 млн руб. Доходность безрискового актива за месяц — 0,5%. Определим одномесячные ожидаемые потери (V@R) нового портфеля (в млн руб.) с уровнем доверия 95%. Распределение стоимости портфеля будем считать нормальным.

Для рисковой части портфеля.

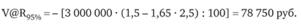
За то же время безрисковый актив принесет прибыль.

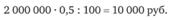
В сумме ожидаемые потери составят.

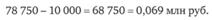
В соответствии с методиками JP Morgan RiskMetrics считается, что волатильность, а пропорциональна корню квадратному из продолжительности временно? го горизонта, для которого рассчитывается V@R. Поэтому, если волатильность известна для одного срока, a V@R нужно найти для другого срока, следует умножать ее на корень квадратный из отношения второго срока к первому. Кроме того, на коротких и средних сроках, следуя RiskMetrics, математическое ожидание дневной доходности полагается равным нулю.

Пример 11.10

Величина V@R для заданного портфеля финансовых инструментов, рассчитанная с уровнем доверия 95% и временны? м горизонтом 1 день, составляет 1 млн руб. Какой примерно будет величина VaR этого портфеля для уровня доверия 99% и временного горизонта 10 дней, если дневные доходности независимы и нормально распределены?

Решение:

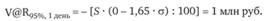
Тогда.

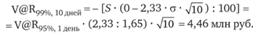
Исторический способ расчета V@R основан на использовании имеющихся исторических данных о стоимости или доходности портфеля. Соответствующая выборка должна быть достаточно большой (желательно, несколько сотен наблюдений), чтобы на ее основе можно было делать выводы о распределении значений и оценивать вероятность того, что в будущем эти значения окажутся в определенных пределах. Алгоритм сводится к следующим действиям:

• 1) принять имеющиеся наблюдения (N штук) за 100%;
• 2) для заданного уровня доверия р% рассчитать соответствующее ему количество наблюдений Np = N • р : 100;
• 3) отсчитывать наблюдения, начиная с наилучших исходов, пока их число не станет равным или превысит Np;
• 4) наихудший уровень потерь, соответствующий последнему учтенному наблюдению, равен р%-ному V@R.

Пример 11.11

После проведения исторических симуляций распределение приращений стоимости портфеля имеет такой вид:

Оценим ожидаемые потери портфеля (в тыс. руб.) с уровнем доверия 90%.

Решение:

Всего имеется.

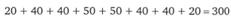наблюдений.

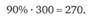
В 280 случаях приращение стоимости портфеля составляло 15 тыс. руб. или более.

Ожидаемые потери не превысят 15 тыс. руб. с вероятностью 90%.

Применение метода V@R к нахождению оптимального портфеля

Пусть у инвестора имеются обязательства в размере U, которые должны быть погашены в конце некоторого периода. Для их покрытия в начале указанного периода инвестируется капитал S. Предполагается, что распределения доходности всех эффективных портфелей нормальны. Среднее ожидаемое значение доходности 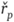и ее стандартное отклонение ар зависят от выбора портфеля р. Задача ставится следующим образом: определить минимальный капитал S и соответствующий портфель р, которые обеспечат покрытие обязательств с вероятностью 1 — ?.

Из свойств нормального распределения следует, что S находится из условия.

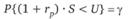
или.

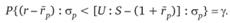
Здесь случайная величина распределена стандартно нормально. Следовательно.

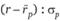
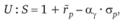
где ??, — квантиль стандартного нормального распределения уровня ?.

Таким образом, критерий выбора инвестиционного портфеля состоит в максимизации величины.

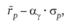
где? зависит от уровня доверия. При у 0.

Получается семейство кривых безразличия в виде прямых линий с положительным наклоном, зависящим от ?. Оптимальный портфель будет точкой касания одной из прямых с эффективной границей, и его положение на этой границе зависит от уровня доверия: чем бо? льшая требуется уверенность в результате (т.е. чем меньше у), тем больше ??, больше наклон кривых безразличия, оптимальный портфель получается более консервативным, а начальный капитал S — бо? льшим.