Расчет рам на действие температуры

Расчет на действие температуры будем производить исходя из предположения, что от совокупности нагрузок и температуры все элементы рамы работают в пределах упругих деформаций. Это позволяет выполнять расчет отдельно от действия нагрузок и от действия температур, а затем суммировать результаты.

Канонические уравнения метода сил при расчете на действие температуры будут иметь следующий вид:

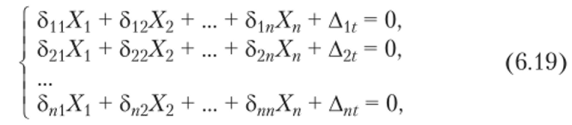
где Д_1г, Д₂г,А_{п (} — перемещения в основной системе по направлению лишних неизвестных от действия температуры. Коэффициенты вычисляются так же, как при расчете на действие нагрузки.

После решения канонических уравнений окончательная эпюра моментов строится на основании равенства.

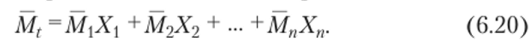
Заметим, что в основной системе (являющейся статически определимой системой) от действия температуры возникают только перемещения, а внутренние усилия равны нулю. Последние возникают только в статически неопределимых системах.

Пример 1. На рис. 6.21, а показана статически неопределимая рама. Температура внутри помещения +20°С, снаружи — 8 °C. Жесткости обоих стержней одинаковы и равны EJ. Длины элементов показаны на чертеже. Высота сечения ригеля h = 0,4 м,.

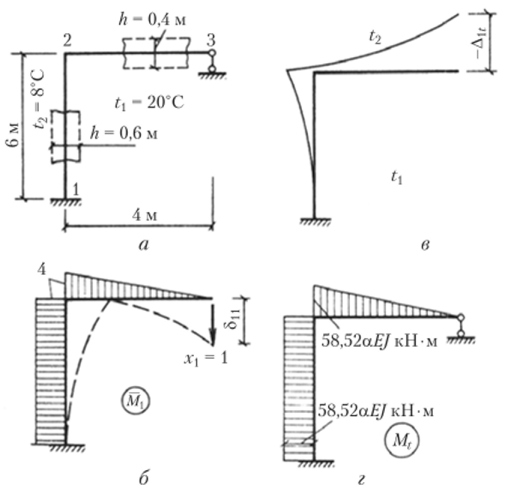
стойки h = 0,6 м. Основная система и эпюра изображены на рис. 6.21, б. На этом же рисунке пунктиром показано деформированное состояние рамы от неизвестного Х = 1. На рис. 6.21, б показано состояние рамы от действия температуры. По эпюре М находим.

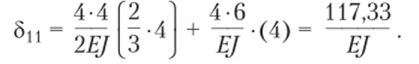
По формуле (5.33) имеем.

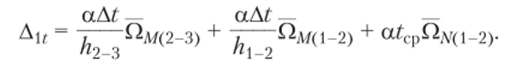
Два первых слагаемых учитывают температурные деформации, создающие искривление стержня^ третье слагаемое учитывает удлинение стойки (для ригеля Ц-⁼ 0). Вычисления дают.

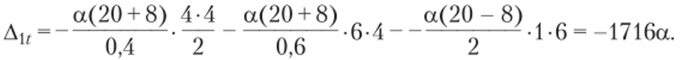
Знак «минус» перед первыми двумя слагаемыми взят потому, что кривизны от действия Х = 1 и температуры разных знаков (см. рис. 6.21, б и в). Третье слагаемое также оказалось отрицательным, так как от действия силы Х = 1 стойка укорачивается, а от температурного воздействия удлиняется.

Каноническое уравнение 8цХ + А_и = 0 имеет решение.

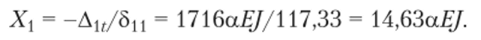
Окончательная эпюра показана па рис. 6.21, г. Обратим внимание на то, что моменты и жесткости выражены в одних и тех же единицах — килоньютонах на метр.

Пример 2. Рассмотрим замкнутый четырехугольник, обладающий двумя осями симметрии х—х и у—у (рис. 6.22, а). Основная система с гремя лишними неизвестными показана на рис. 6.22, б. Два из них Х и Х₂ симметричны относительно оси у—у у а третье Х₃ — кососимметричное. Температура внутри контура равна t = 20 °C, а наружная температура для всех четырех стержней одинакова и равна -10°С. В целом температурное воздействие симметрично относительно обеих осей симметрии. Вследствие сказанного кососимметричное неизвестное = 0. Остается определить два неизвестных Х и Х₂. Единичные эпюры М1, М₂ и N[_t N₂ от каждого из них показаны на рис. 6.22, в — е. По ним находим.

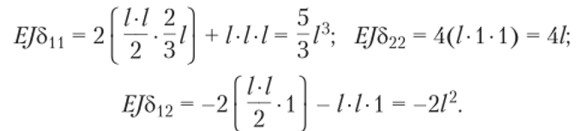
Рис. 6.22.

Далее имеем: At = 20 — (-10) = 30 °C; ?_ср = (20 — 10)/2 = 5 °C; h_{ = h₂ = h = ^ = ОД/.

По формуле (5.33) находим.

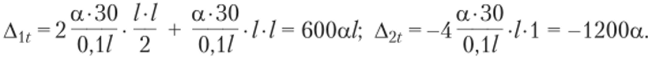
В выражениях для А_и и Д_2г знаки определены путем сравнения деформаций от единичных значений неизвестных и от температуры. Так, например, первое слагаемое в выражении для А_и имеет знак «плюс», так как кривизны от температуры и от нагрузки имеют одинаковые знаки, а у Д₂, — разные знаки. Второе слагаемое в обоих перемещениях равно нулю, так как Q. vB общих случаях равна нулю.

Канонические уравнения будут.

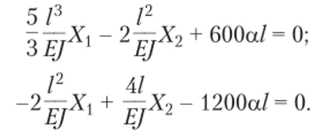
Если второе уравнение умножить на ½ и сложить с первым, то получим Х = 0.

Таким образом, Х = 0, Х₂ = 300аEJ/1.

Полученный результат не является неожиданным. Дело в том, что система симметрична относительно двух осей. При температурном воздействии, также симметричном относительно двух осей, окончательная эпюра моментов должна быть симметричной, но отношению к обеим осям. Такая симметрия возможна только при Х = 0, так как эпюра симметрична только относительно одной оси. Окончательная эпюра М₍ показана на рис. 6.22, ж.

При проверке правильности построения М_г следует обратить внимание на то, что применявшийся ранее способ, по которому результат перемножения окончательной эпюры моментов на какую-либо из единичных эпюр равнялся нулю, недействителен:

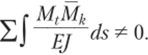
Результат такого перемножения даст только ту часть канонического уравнения, которая содержит неизвестные Х, Х₂, Х_п. Однако в каноническом уравнении содержится также слагаемое A_t, поэтому.

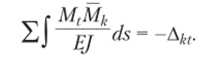
Это равенство и будет являться проверкой эпюры M_t.