Вероятность. 
Политический анализ и прогнозирование. 
Часть 1

Означает ли невозможность точно предсказать значения случайной переменной невозможность выявить количественные закономерности в ее поведении? Разумеется, нет; в противном случае существование статистики как науки было бы невозможным. Так, при подбрасывании игральной кости нельзя точно предсказать результат каждого конкретного броска. Однако некоторые общие характеристики достаточно большой серии бросков вполне поддаются прогнозированию, более того — с очень высокой степенью точности. Точно так же мы потерпим поражение, пытаясь точно предсказать выбор каждого конкретного избирателя; однако мы вполне в состоянии численно оценивать общие свойства электоральных предпочтений большой группы избирателей. И уже на основании этих общих свойств мы можем строить вероятностные оценки поведения отдельных ее представителей.

Чтобы дать определение вероятности, необходимо ввести еше несколько понятий. Элементарными исходами (элементарными событиями) являются результаты случайного испытания, которые нельзя разложить на составляющие и которые взаимно исключают друг друга. Например, выпадения орла при подбрасывании монеты или двойки при броске игральной кости являются элементарными исходами. Если мы припишем этим исходам числа (например, орел — 1, решка — 0), получатся значения номинальной переменной. Переменная является номинальной потому, что орел и решка — качественно разные исходы. Приписанные им числа не отражают никакого количественного смысла.

Элементарные исходы обозначаются обычно греческой буквой со («омега» строчная). Все мыслимое множество таких неразложимых на составные части результатов называется пространством элементарных исходов и обозначается греческой буквой ?2 («омега» заглавная). Так, для случайного испытания по подбрасыванию игрального кубика пространство элементарных исходов следующее:

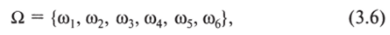
где со, соответствует числу выпавших очков. Для однократного подбрасывания монеты ?2 = {(0[, со₂}, где со, — орел, о>2 — решка. Для одновременного броска двух монет ?2 = = {со, со₂, со₃, со₄}, где со, соответствует орлу на первой монете и решке на второй; сог — решке на первой монете и орлу на второй; со, — орлам на обеих монетах; со₄ — решкам на обеих монетах. Порядок нумерация исходов, вообще говоря, не важен; важно, чтобы выполнялись условия взаимной исключаемости и неразложимости на более элементарные составляющие.

В каждом из приведенных примеров пространство элементарных исходов дискретно, состоит из отдельных результатов, которые можно перечислить. Однако оно может быть и непрерывным. Например, на выборах пространство элементарных исходов для отдельной партии представляет собой (по крайней мере, теоретически) непрерывное множество от 0 до 100% голосов избирателей:

Событие может совпадать с элементарным исходом, но в более общем случае оно представляет собой некоторую их совокупность, подмножество множества И. Событие (обозначается большой латинской буквой) «выпало четное число очков» (А) не является элементарным, так как оно «раскладывается» на три составляющих, соответствующих выпадению двойки, четверки и шестерки: А = {со₂, со₄, со₆}. В теории вероятностей говорят, что элементарные исходы «выпало два», «выпало четыре» и «выпало шесть» благоприятствуют событию «выпало четное число очков». Это означает, что реализация любого из этих исходов приводит к реализации события А.

Событие «выпало четное число очков» является случайным: оно может произойти или не произойти. Если событие происходит всегда, оно называется достоверным и совпадает с пространством элементарных исходов: А = П. Например, таковым является событие «выпало четное или нечетное число очков». Событие, которое не происходит никогда, называется невозможным и обозначается 0 (пустое множество). Так, событие «выпало четное и нечетное число очков в результате одного броска» является невозможным.

Событиям может быть сопоставлено число, являющееся мерой возможности их реализации, — вероятность. Вероятность события обозначается большой латинской буквой Р_у в скобках после нее указывается событие, вероятность которого оценивается: например, Р{А). Это очень напоминает школьную запись у =/(?*)> и действительно: вероятность — это функция. Как числовая функция вероятность обладает следующими основными свойствами.

• • Вероятность любого события принимает значения между нулем и единицей: 0 < Р (А) < 1. Отметим, что часто используемая в обиходной речи «процентная» характеристика вероятностей в научном смысле не вполне корректна.
• • Вероятность достоверного события равна единице: Р (П)= 1.
• • Вероятность невозможного события равна нулю: /40) = 0.

В целом, в теории вероятностей выделяется четыре подхода к ее формальному определению: классический, статистический, геометрический и аксиоматический. Мы остановимся на классической и статистической вероятности; понимание первой требуется для изучения общих основ, вторая же представляет собой один из важнейших математических инструментов анализа данных.

С классической вероятностью мы имеем дело в тех испытаниях, в которых элементарные исходы равновозможны. Так, при подбрасывании монеты мы с равной возможностью ожидаем выпадения орла и решки. Это заложено в условиях испытания: монета должна быть «правильной», не обладать смещенным центром или каким-то другим свойством, обусловливающим тот или иной элементарный исход. О таких испытаниях говорят, что они обладают симметрией элементарных исходов.

Свойство равновозможности позволяет нам определить классическую вероятность наступления события А как отношение числа элементарных исходов, благоприятствующих событию, к общему числу элементарных исходов:

где п_А — число исходов, благоприятствующих событию Л_у п — общее число исходов.

Пусть в испытании, представляющем собой однократное подбрасывание игральной кости, интересующим нас событием является выпадение четного числа очков. Ему благоприятствует три элементарных исхода: двойка, четверка и шестерка. Общее число возможных исходов — шесть. Вероятность выпадения четного числа является отношением 3/6 или 0,5. Аналогичным образом, вероятностью события «выпало число очков меньше трех» является 2/6 или 1/3, так как ему благоприятствует два исхода из шести возможных.

Рассмотрим тот же пример через призму измерительных шкал. Событие А представляет собой переменную номинального уровня измерения с двумя значениями, соответствующими выпадению решки и орла. А — случайная переменная, но не случайная величина, так как величина — это параметрическая, а не категориальная числовая характеристика. А вот п_А — число благоприятствующих исходов — это случайная величина, измеренная по шкале отношений. Когда мы работаем с качественно разными исходами, для получения случайной величины нам требуется их каким-то образом посчитать. Поэтому в формальном смысле случайная величина представляет собой числовую функцию, определенную на пространстве элементарных исходов.

Еще раз на другом примере: «пол респондента» — случайная переменная, принимающая два значения (например, 1 — мужчина, 2 — женщина). Но это не случайная величина. «Количество мужчин в изучаемой совокупности» — случайная величина.

К сожалению, классическая вероятность имеет очень ограниченное применение в политическом анализе. Причина в том, что в политике мы почти не имеем дела с симметричными испытаниями, элементарные исходы которых равновозможны. Например, испытание состоит в получении ответов респондентов на вопрос об оценке существующего политического курса. Элементарные исходы следующие: со, — «оцениваю крайне отрицательно», 002 — «оцениваю отрицательно», со₃ — «оцениваю положительно», со₄ — «оцениваю высоко положительно». Применив классическую схему, мы оценим вероятность события «получена положительная оценка» как 2/4 (или 0,5): ему благоприятствует два исхода (Л = {со₃, со₄}) из четырех. Если бы такой расчет имел какойто смысл, были бы сэкономлены очень значительные средства, затрачиваемые на социологические опросы: их попросту не нужно было бы проводить. Однако очевидно, что появление каждого варианта ответа обладает далеко не одинаковой возможностью. Реальное распределение ответов будет зависеть, как минимум, от проводимого политического курса и от характеристик разных групп респондентов, влияющих на их восприятие политики. Образно говоря, в политике мы имеем дело с «неправильными» монетами и игральными кубиками.

Для расчета вероятности событий в несимметричных испытаниях используется статистический подход; получаемое число будет называться, соответственно, статистической вероятностью. Она имеет экспериментальную природу. В «классическом» случае мы могли ни разу не подбросить монету и, тем не менее, определить вероятность выпадения орла. В статистическом случае невозможно рассчитать вероятность события без проведения серии испытаний. Причем, как будет показано далее, чем большее число испытаний включает серия, тем более обоснованную оценку вероятности мы получим.

Расчет статистической вероятности основан на подсчете частоты интересующего нас события при проведении серии испытаний. Частота (обозначается латинской буквой п) показывает, сколько раз встречается данное событие в серии, это результат счета. Как мы указывали выше, в результате счета мы всегда получаем случайную величину.

Пусть для приведенного выше примера с отношением к политическому курсу мы имеем следующие частоты (количество респондентов, давших именно такой ответ на вопрос, табл. 3.2).

Таблица 3.2

Располагая частотами каждого события, можно рассчитать относительные частоты, представляющие собой отношение частоты данного события к общему числу испытаний, или суммарной частоте: 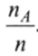. В нашем примере опрошено 1000.

респондентов (в статистическом смысле проведено 1000 испытаний — или зарегистрировано 1000 наблюдений) и относительные частоты составят соответственно: 200/1000 = = 0,2; 300/1000 = 0,3; 400/1000 = 0,4; 100/1000 = 0,1. Понятие относительной частоты — ключевое в определении статистической вероятности. Последняя представляет собой предел относительной частоты события, когда число испытаний стремится к бесконечности:

Это строгое математическое определение статистической вероятности имеет один существенный недостаток: работая с реальными данными, мы будем иметь лишь ограниченный (часто очень ограниченный) и фиксированный набор чисел и не сможем определить, что произойдет при устремлении числа случаев к бесконечности. Поэтому для решения практических задач анализа пользуются формулой оценки вероятности Р (Л) И в этом случае все совсем просто: оценка статистической вероятности события равна его относительной частоте:

Если в практических исследованиях вероятность — это всего лишь относительная частота, зачем обращать внимание на значительно менее ясную формулу (3.9)? На самом деле различие между моделями (3.9) и (3.10) очень важно: это одно из проявлений фундаментального для статистического мышления различения истинных (закономерных) значений параметров и их оценок. Мы разберем его подробно на простом примере.

Возьмем испытание с однократным броском монеты. Оно обладает равновозможными исходами, поэтому мы можем рассчитать вероятность по классической схеме. Для этого разделим 1 — число исходов, благоприятствующих событию «выпал орел», на общее число исходов — 2 и получим ½, или 0,5. Причем это «истинная», закономерная вероятность в том смысле, что она заложена в самих условиях эксперимента; «правильная» монета «устроена» таким образом, что при добросовестном броске ложится с равной вероятностью на каждую из сторон.

Для дискретных переменных сумма вероятностей всех значений, которые она может принимать, равна единице: 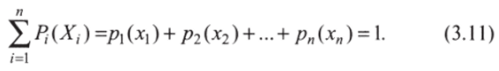^[1]

Оператор суммирования 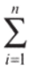показывает, что складываются числа от 1 до //. В нашем примере сумма вероятностей выпадения орла (0,5) и решки (0,5) равна 1.

Теперь представим, что мы не знаем о симметричности этого испытания или подозреваем нечестную игру. Попытаемся оценить вероятность выпадения орла статистически, т. е. по результатам серии бросков. Результаты испытаний будем записывать в таблицу, где для каждого испытания будем фиксировать:

• • п — общее число проведенных испытаний; с каждым броском оно будет увеличиваться на единицу; фактически, п будет отражать номер испытания;
• • Л — результат испытания, причем выпадению орла («успех») будем приписывать значение 1, выпадению решки — 0 (понятие «успеха» в статистике не имеет оценочной нагрузки, мы лишь отмечаем, что произошло какое-то определенное событие);
• • п_А — общую (накопленную) частоту выпадения орла; с каждым успехом она будет увеличиваться на единицу;

п_А Д.

• —-Р — относительную частоту выпадения орла, явля;

п

ющуюся одновременно оценкой вероятности этого события.

Результаты испытаний для броска монеты могут выглядеть, например, так (см. табл. 3.3).

После десяти бросков статистическая оценка вероятности составляет 0,4, после двадцати — 0,45, после тридцати — 0,48, после пятидесяти — 0,49. С увеличением числа испытаний оцененное значение стремится к истинному значению, — в этом суть формулы (3.9). В нашем примере статистическая вероятность стремится к классической вероятности, если число испытаний устремлено к бесконечности. Кроме того, этот пример показывает, почему в статистике важно иметь многократные испытания. Чем больше число случаев, тем надежнее получаемые оценки, тем ближе они к истинным, закономерным значениям. Данный принцип иллюстрируется на графике (рис. 3.1), где по оси абсцисс отложено число испытаний л, по оси ординат — оценки вероятности выпадения орла.

Разумеется, конкретные значения Л, соответствующие выпадению орла, в разных сериях испытаний будут разТаблица 3.3

Относительные частоты округлены до третьего знака после запятой.

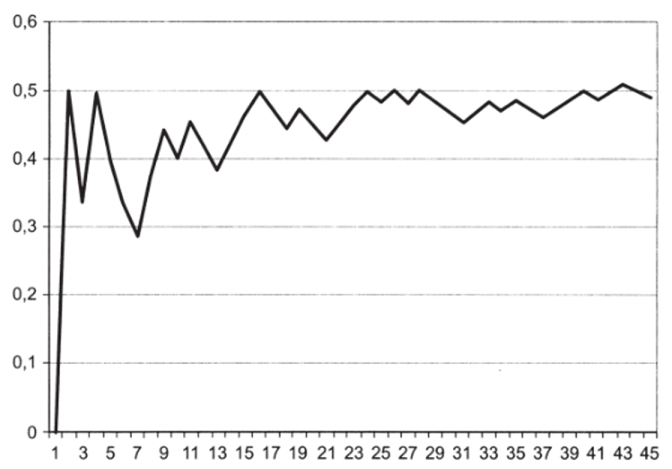
Рис. 3.1

личаться. Говоря более научно, каждая серия испытаний будет давать нам иную реализацию случайной переменной А, а вслед за ней — и случайных величин п_А и njn. Соответственно, в результате вы получите другой график зависимости статистической вероятности от числа испытаний. Но общий принцип — сходимость относительной частоты к значению 0,5 — останется без изменений, так как это значение является закономерным. Статистику в целом можно охарактеризовать как науку, которая ищет закономерности в таких явлениях, где присутствует случайная составляющая.

Можно было бы провести эксперимент с реальной монетой, но мы поступим иначе. Построим компьютерную модель броска монеты с помощью программы Excel. Для этого упражнения (как и для многих других в этой книге) необходимо, чтобы в Excel была установлена надстройка «Пакет анализа». Чтобы ее установить, в версиях до 2003 г. включительно необходимо войти в меню «Сервис» и в нем найти опцию «Надстройки». В более поздних веосиях программы следует щелкнуть мышкой по значку в левом верх нем углу и найти опцию «Параметры Excel». В параметрах выберите «Надстройки», в надстройках — «Пакет анализа» (рис. 3.2).

Рис. 3.2.

Упражнение 3.1

• 1. Озаглавьте столбец, А «Значения». «Успеху» соответствует значение 1, иному исходу — значение 0.
• 2. Озаглавьте столбец В «Вероятности». При броске монеты вероятность успеха («орел») составляет 0,5, равно как и вероятность неуспеха.

Таблица 3.4

В результате получим табл. 3.4.

3. Войдите в меню «Данные», в нем выберите «Анализ Данных» (в версиях до 2003 г. —.

«Сервис / Надстройки / Пакет анализа или Анализ данных»). Среди «инструментов анализа» выберите позицию «Генерация случайных чисел» (рис. 3.3).

Рис. 3.3.

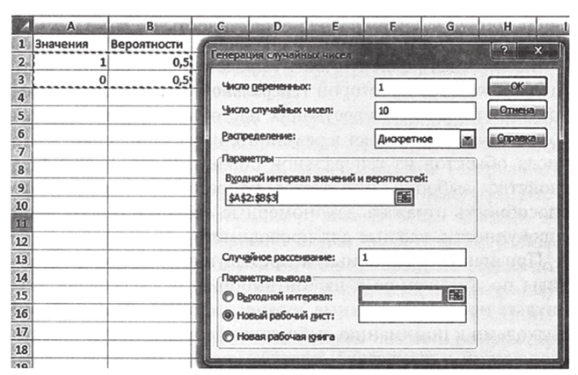
Рис. 3.4.

Рис. 3.5.

ваться нужной функцией =СЧЕТ (А1 :А 10). Эта функция пересчитывает все числовые значения в заданном интервале.

8. Наконец, по формуле статистической вероятности (3.10) разделим число успехов на число испытаний.

В моем случае оценка вероятности равна 0,4. У вас почти наверняка получится другое число, так как реализация случайной переменной в столбце, А будет отличаться от той, что на рис. 3.5. Но по мере увеличения числа испытаний п оценка статистической вероятности будет все ближе подходить к закономерному значению 0,5.

• [1] Здесь и в дальнейшем знаком «крышки» мы будем обозначать оценкунекоторого параметра.