Итерационные методы уточнения корней

Метод простой итерации Применим принцип сжимающих отображений для уточнения значения корня уравнения. Для этого заменим уравнение (1) равносильным уравнением.

(4).

Сделать это можно множеством способов. Простейший и очевидный — добавить х к левой и правой частям уравнения (4).

Пусть — корень уравнения (4), а — полученное каким — лио способом на этапе отделения корней грубое приближение к корню. Подставляя в правую часть уравнения (4), получим некоторое число. Проделаем то же самое с, получим и т. д. последовательно применяя рекуррентное соотношение образуем итерационную последовательность:

(5).

Процесс построения итерационной последовательности имеет простую геометрическую интерпретацию. На рис. 6. изображены два случая, показывающие, что последовательность приближений может быть как сходящейся, так и расходящейся. Как следует из принципа сжимающих отображений, условием сходимости итерационной последовательности является то, что функция осуществляет сжимающее отображение в окрестности корня.

Предположим, что существует отрезок, содержащий все члены последовательности (5). Если на отрезке функция возрастает, то итерационная последовательность является монотонной. Если убывает, то она является колеблющейся.

Условие того, что функция является сжимающей функцией на отрезке, приобретает в данном случае следующий вид: для всех, а также существует такое число, что для любых х, выполняется соотношение.

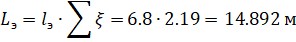
(6).

Условие (6) имеет в математической литературе собственное название: условие Липщица.

Однако практически проверить выполнимость условия Липщица весьма затруднительно. Для этого следовало бы перебрать все возможные пары значений (x, y) из отрезка, что практически невозможно. Применим теорему Лагранжа для (6), которая гласит, что если функция дифференцируема на отрезке, то на нем найдется такая точка с, что будем иметь формулу:

(7).

Называемая формулой Лагранжа (или формулой конечных приращений) Сравнивая (6) и (7) приходим к выводу: если существует такое число, что для любых.

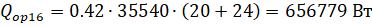
(8).

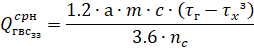
то функция является сжимающей на отрезке. При этом роль константы Липщица играет .

Итак, общая схема решения уравнения (1) методом итерации такова:

• 1. Выполнить, полностью или частично, отделение корней. Выбрать тот корень, который принадлежит уточнению, и соответствующий ему отрезок, содержащий этот корень и не содержащий иных корней данного уравнения.
• 2. Преобразовать уравнение (1) к равносильному уравнению вида (4).

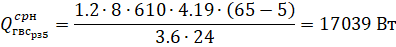
• 3. Найти и проверить, является ли функция сжимающей на отрезке .
• 4. Если сжимаемость имеет место:

a) Задаться точностью е нахождения приближенного значения корня;

b) Задаться первым членом итерационной последовательности — начальным приближением к корню;

c) Построить следующий член итерационной последовательности (6);

d) Всякий раз, получив очередной член итерационной последовательности, проверять, выполняется ли условие: или.

(9).

e) Если условие (9) выполняется, то принять за результат, иначе вновь выполнить пунк с).

Принятие в качестве результата, полученного с точностью е, означает, что вместо полной погрешности решения использована погрешность метода.

Если подбирать вслепую, можно пустую потратить массу времени. Есть общие приемы, которые позволяют избежать этой ситуации.

Рассмотрим простейший из них. Преобразуем уравнение (1) к равносильному уравнению.

(10).

где — константа, отличная от нуля.

Таким образом,. Условие (8) приобретает вид, или, иначе.

(11).

Если удастся подобрать значение так, чтобы условие (11) выполнялось, то метод итераций применим.

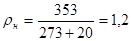
Рассмотрим в начале случай, когда. Второе из неравенств (11) сводится к условию > 0, а первое — к условию. Полагая.

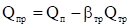
(12).

Получим из (10) итерационную формулу.

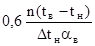
(13).

Критерий выхода из итерационного процесса:

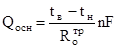
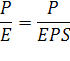
Поскольку считается, что, то, где .

Если, то, рассуждая аналогично, получим и итерационную формулу.

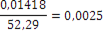
(14).

Уточнить корень уравнения методом простой итерации на отрезке [0,4;0,5] с заданной точностью.

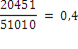
Исходное уравнение можно привести к виду, в этом случае. Подберем константу из условия (12). Поскольку производная на отрезке положительна и монотонно возрастает, то достигает максимума в точке 0,5.. Следовательно, положим. Таким образом, имеем рекуррентное соотношение Найдем критерий выхода из итерационного процесса:

.

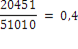
где .

Малое значение q обеспечивает быструю сходимость итерационного процесса.

Программа на языке Turbo Pascal имеет следующий вид, также сразу покажем результат работы программы: