Алгоритмы бикластерного анализа

В данном разделе мы рассмотрим два подхода к бикластерному анализу матриц. Первый был представлен в статье Диллона «Co-clustering documents and words using Bipartite Spectral Graph Partitioning», а второй в статье Бориса Миркин и Андрея Крамаренко «Approximate Bicluster and Tricluster Boxes in the Analysis of Binary Data». Также здесь представлен новый жадный алгоритм, основанный на результатах работы Миркина и Крамаренко.

1) Спектральное разложение двудольного графа.

В статье «Co-clustering documents and words using Bipartite Spectral Graph Partitioning» Диллон предложил идею одновременной кластеризации текстов и ключевых слов. Эта идея строится на том, что типичная схема кластеризации документов основана на идее представления документов в виде векторов ключевых слов с весами (релевантностями). В то же время, кластеризация слов часто основывается на симметричной модели: слова сравниваются по векторам их принадлежности к документам в коллекции.

Такая симметричность подходов кластеризации двух типов объектов подтолкнула Диллона к рассмотрению совместной модели: двудольный граф, где вершинами выступают слова (в одной части графа) и тексты (в другой части). Рёбра в таком графе означают принадлежность слова к тексту, а веса могут быть назначены по различным метрикам релевантности, например, одной из рассмотренных выше.

Задача разбиения такого графа на две части (два кластера) становится задачей нахождения минимального разреза в графе. Разрез вершин на два подмножества вершин определяется как:

.

где — это матрица смежности графа. На основе этого определяется вес разреза для большего количества подмножеств вершин:

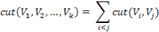
Рассмотрим теперь общую матрицу релевантности слово/текст A. Заметим, что матрицу смежности соответствующего двудольного графа можно записать как:

.

где вершины графа расположены так, что сначала идут вершины, соответствующие словам, а затем вершины для документов.

Теперь, чтобы определить понятие «сбалансированного» разреза нужно ввести диагональную матрицу W, для которой элементы равняются весам вершин в графе. Вес подмножества вершин определяется как сумма весов всех его вершин. После этого вводится следующий критерий для минимизации:

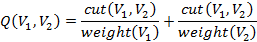
Заметим, что такой критерий был до этого предложен Ши и Маликом для решения задачи о разбиении произвольного графа (необязательно двудольного). Этот критерий позволяет говорить о разбиении с сбалансированными весами частей. В дополнение, Диллон доказывает следующую теорему о векторе разбиения q:

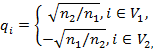
где. Такой вектор q удовлетворяет уравнению:

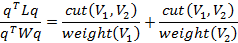
Матрица L в данном уравнении является матрицей Лапласа и определяется как:

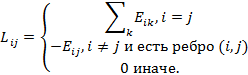
Отсюда получаем, что необходимо минимизировать функцию:

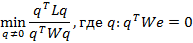
Утверждается, что минимум достигается, когда q — это собственный вектор, соответствующий второму по величине (снизу) собственному числу:

— искомое собственное число. Вместо того, чтобы искать собственный вектор, Диллон прибегает к понятиям сингулярных векторов матрицы и показывает, как пользоваться методом сингулярного разложения для матрицы Лапласа на основе двудольного графа. Определим диагональные матрицы :

— сумма весов рёбер смежных со словом i,.

— сумма весов рёбер смежных с текстом j.

Диллон доказал, что задача нахождения собственного вектора матрицы L, отвечающего второму наименьшему собственному числу эквивалентно задаче нахождения левого и правого сингулярных векторов матрицы, соответствующих второму наибольшему сингулярному числу.

А второй собственный вектор матрицы L равен:

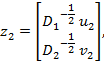
где — левый и правый сингулярные векторы матрицы соответственно.

Для решения задачи разбиения графа на два бикластера, необходимо, чтобы вектор разбиения был бимодальным, то есть содержал в качестве значений только два числа. Для того, чтобы привести вектор к такому виду, автор статьи предлагает обработать его алгоритмом k-средних (k-means clustering), то есть центры двух кластеров будут как раз выступать в роли двух значений итогового вектора разбиения. Для нахождения большего количества бикластеров Диллон предлагает использовать сразу несколько сингулярных векторов (по количеству требуемых кластеров) и подавать их как матрицу на вход алгоритма k-средних.

Программная реализация данного метода присутствует в довольно популярной библиотеке алгоритмов машинного обучения для Python — Scikit-Learn. Эта реализация и была использована в данной работе для предоставления метода спектрального разложения двудольного графа.

2) «Коробочная» кластеризация — BBox.

Для удобства будем считать, что матрица связей между объектами имеет бинарный вид, то есть матрица содержит единицу, если соответствующие два объекта связаны между собой, и ноль в противном случае. Пусть дана матрица R =, где — объекты первого типа, — объекты второго типа, тогда назовём бикластером пару подмножеств, , таких, что:

.

при этом нельзя расширить подмножества V или W, не нарушив это свойство.

Однако такое ограничение на все единицы на пересечении двух подмножеств кажется слишком сильным условием. Поэтому Миркин и Крамаренко предложили модель бикластеризации, которая для каждого бикластера стремится минимизировать остатки следующего вида:

.

где — остаток, l — константа для бикластера, а и — бинарные векторы принадлежности множествам V и W соответственно, то есть тогда и только тогда, когда. Данная модель приводит к следующему критерию для минимизации суммы квадратов остатков:

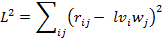
В свою очередь, было показано, что данный критерий привёл к оптимальному l, равному плотности бикластера:

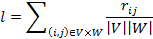
Что привело авторов к основному критерию для максимизации:

Можно видеть, что в представленной здесь модели не используется тот факт, что матрица является бинарной, а значит, модель может быть легко обобщена для матриц небинарного вида. На основе данного критерия Миркин и Крамаренко предложили алгоритм нахождения оптимального бикластера для заданной начальной строки бинарной матрицы:

Алгоритм BBox (i):

• 1. Инициализация: V = {i}, W = {j| };
• 2. Для всех ;
• 3. Для всех ;
• 4. Для всех ;
• 5. Для всех ;
• 6. Найти максимум среди всех и, и, если он больше, добавить/удалить соответствующую строку/столбец из бикластера, после чего перейти к шагу 2. Иначе вернуть текущий бикластер.

В дополнение, авторы статьи показали, что для бикластера, найденного по алгоритму BBox, верно следующее:

• · Для всех плотность однострочного бикластера меньше половины плотности всего бикластера ;
• · Для всех плотность однострочного бикластера больше или равна половине плотности бикластера ;
• · Аналогичное свойство выполняется и для столбцов матрицы.

Данная модель бикластеризации была также обобщена авторами для нахождения трикластеров и даже кластеров большей размерности (P-кластеры).

1) Новый жадный алгоритм.

Более формально, представленные выше свойства оптимального бикластера, найденного алгоритмомо BBox, можно записать так:

• · ;
• · ;
• · ;
• · .

Здесь .

Основываясь на этих свойства, мы теперь предлагаем новый жадный алгоритм бикласетризации:

Алгоритм GreedyBBox.

Вход: матрица и индекс начального ряда k.

Выход: бикластер

• 1. ;
• 2. ;
• 3.
• 4. Добавить все ряды к, для которых ;
• 5. Удалить все столбцы из, для которых ;
• 6. ;

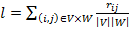
• 7. ;
• 8.
• 9. Если перейти к шагу 3, иначе вернуть бикластер .

В данном алгоритме на каждом шагу мы либо добавляем новые ряды в бикластер, удаляем столбцы из бикластера или делаем и то, и то. Это означает, что для входной матрицы размером алгоритм сделает не более операций. Для квадратной матрицы, как в случае с матрицей схожести между ключевыми фразами, алгоритм выполнит не более итераций, если сама матрица порядка. Отсюда следует, что общая сложность алгоритма равна, так как подсчёт плотности для одного ряда/столбца имеет сложность порядка, а подсчёт изменённой плотности можно производить при каждом удалении/добавлении столбца/строки в билкастер за. Например, если добавить новый ряд с плотностью равной, то изменённую плотность всего бикластера легко посчитать по формуле:

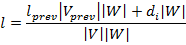
Данный алгоритм можно также применять к транспонированной матрице, так как он работает несимметрично в отношении столбцов и строк. При бикластерном анализе матрицы релевантности фраза/текст такое поведение — расширение по рядам и сужение по столбцам — кажется выгодным. В самом деле, нам интересны большие группы ключевых слов, релевантные для сравнительно малых групп текстов, то есть потенциальных доменов в таксономии.

В силу того, что алгоритм GreedyBBox основан на жадном итеративном подходе, получаемые бикластеры могут быть похожи на локальные оптимумы, получаемые алгоритмом BBox, но, всё же, несколько отличаться. В ходе экспериментирования над аннотациями к научным статьям было замечено, что среди бикластеров, полученных алгоритмом GreedyBBox, содержится очень большое число похожих бикластеров — отличающихся на один-два элемента по строкам и/или столбцам. В связи с этим, полученные бикластеры фильтруются на основе схожести между ними. Схожесть между бикластерами высчитывается на основе коэффициента Жаккарда:

.

.

где — сравниваемы между собой бикластеры. Таким образом, бикластеры считаются схожими, если коэффициент Жаккарда для рядов и коэффициент Жаккарда для столбцов двух бикластеров выше некоторого порогового значения. Если два бикластера схожи, то при фильтрации оставляется тот, для которого выше параметр .

2) Мемоизация в BBox.

Помимо нового алгоритма бикластеризации, в данной работе была предпринята попытка ускорить существующий алгоритм BBox при помощи запоминания результатов. При обработке входной матрицы алгоритмом BBox, ему на вход последовательно подаются все строки матрицы в качестве начальных. При этом итоговый оптимальный бикластер, найденный алгоритмом, часто не зависит от индекса входной строки. В связи с этим, кажется разумным для всех промежуточных состояний (промежуточных неоптимальных бикластеров) запомнить конечный результат. В таком случае, на каждой внутренней итерации алгоритма можно проверять, не был ли текущий бикластер уже ранее сформирован для другой начальной строки, и завершить работу с текущей начальной строкой, если был.

Для реализации этой идеи в работе используется хеш-множество, хранящее в качестве элементов финальные и промежуточные бикластеры, полученные на предыдущих итерациях. На роль аргумента для хеш-функции бикластера был выбран параметр, который является основным критерием для максимизации. Таким образом, значение параметра округляется до пятого знака после запятой и подаётся на вход стандартному алгоритму хеширования дробных чисел, реализованному в языке Python. Выбор пал именно на этот параметр, так как он зависит как от значений в подматрице, образованной бикластером (а именно, от среднего значения в подматрице), так и от размера бикластера. В связи с этим, можно ожидать минимальное число хеш-коллизий между различными бикластерами.

Если в какой-то момент на внутренней итерации цикла промежуточный бикластер будет совпадать с уже имеющимся бикластером в хеш-множестве, то все предыдущие промежуточные бикластеры будут добавлены во множество, и алгоритм перейдёт к обработке следующей строки матрицы.