Метод а.н. Крылова

Отыскание собственных значений матрицы

Академик А. Н. Крылов в 1931 году одним из первых предложил довольно удобный метод раскрытия определителя (2).

Суть метода А. Н. Крылова состоит в преобразовании определителя D () к виду.

(1).

Равенство нулю определителя D () есть необходимое и достаточное условие для того, чтобы однородная система линейных алгебраических уравнений.

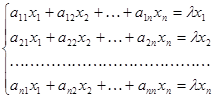
(2).

имела решение х1, х2, …, хn, отличное от нулевого.

Преобразуем систему (2) следующим образом. Умножим первое уравнение на и заменим x1, …, xn их выражениями (2) через x1,…, xn.

Это дает.

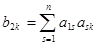
(3) где (4).

Умножим далее уравнение (3) на и заменим снова x1, …, xn их выражениями через x1,…, xn. Получим.

.

Повторяя этот процесс (n-1) раз, мы перейдем от системы (2) к системе.

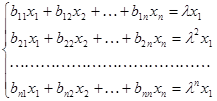
(5).

коэффициенты которой будут определятся по рекуррентным формулам.

(6).

Очевидно, что определитель системы (5) будет иметь вид (1).

Система линейных алгебраических уравнений (5) имеет ненулевое решение для всех значений, удовлетворяющих уравнению D ()=0. Таким образом, D1()=0 при всех, удовлетворяющих уравнению D ()=0.

Покажем, что.

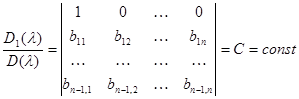
(7).

Пусть все корни D () различны. Так как все корни D () являются корнями D1(), то D1() делится на D (). Так как, кроме того, степени D1() и D () одинаковы, то частное должно быть постоянным. Сравнивая коэффициенты при n, получим.

D1()=СD () (8).

В случае, если D () имеет кратные корни, равенство (8) сохраняется.

Рассмотрим теперь коэффициенты bik, определяющие D1(). Введем в рассмотрение векторы Bi с компонентами bi1, bi2, …, bin. Равенства.

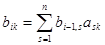
(i=1,2,…, n).

показывают, что Bi=ABi-1, где A — матрица, транспонированная к данной. Из этого следует, что.

Bi=A i-1B1, B1=AB0, (9).

где В0=(1,0,…, 0).

Если С0, то уравнения D1()=0 и D ()=0 эквивалентны. Если же С=0, то это преобразование ничего не дает. А. Н. Крылов предлагает в этом случае особый прием, рассмотренный ниже. Возьмем в качестве вектора В0 произвольный вектор В0=(bi1,bi2,…, bin) и получим с его помощью по формулам (9) векторы Вi.

Пусть u=b01×1+b02×2+…+b0nxn (10).

где x1, x2,…xn — решения системы (1/). Тогда повторяя прежние рассуждения, получим:

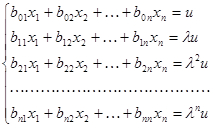
(11).

Решая эту систему как систему линейных однородных уравнений с n+1 неизвестными u, x1, x2,…xn, получим, что ненулевое решение возможно в том и только в том случае, когда.

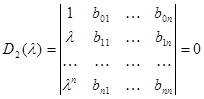
(12).

Повторяя прежние рассуждения, найдем, что.

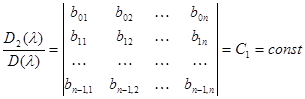
(13).

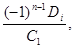
если С10, то коэффициенты рi характеристического многочлена определяются как отношения где Di — алгебраические дополнения элементов n-i в определителе D ().

Но сущность метода Крылова и состоит в том, чтобы находить эти коэффициенты, не подсчитывая миноры.

Воспользуемся теоремой Гамильтона — Кэли о том, что матрица является корнем своего характеристического уравнения, т. е.

(A) n+p1(A)n-1+…+pn-1A+pnE=0, (14).

где рi — коэффициенты характеристического многочлена.

Умножая равенство (14) на b0, получим:

bn+p1bn-1+p2bn-2+…+pn-1b1+pnb0=0 (15).

Это векторное равенство дает систему линейных алгебраических уравнений для определения коэффициентов характеристического многочлена. Определитель этой системы равен С1. Решать полученную систему можно любым из известных методов, например, методом Гаусса.

Можно было бы применить теорему Гамильтона — Кэли и для самой матрицы А, получили бы тогда систему сn+p1сn-1+p2сn-2+…+pn-1с1+pnс0=0 (15/).

здесь ci=Aic0, c0.

— произвольный начальный вектор.

Пример. Пусть матрица A имеет вид:

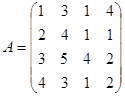
в качестве вектора В0 возьмем вектор В0=(1,0,0,0). Тогда получим векторы.

В1=АВ0, В2=А2В0= АВ1, В3=А3В0=АВ2, В4=А4В0=АВ3:

Система линейных алгебраических уравнений для определения коэффициентов характеристического многочлена имеет вид:

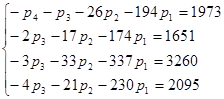
Решив эту систему, получим: р1=-11, р2=7, р3=72, р4=-93. Поэтому характеристический многочлен примет вид:

D ()= 4 -113 + 72 +72 -93.

В приведенном примере С10.

В случае, если С=0, такая система не даст возможности определить коэффициенты характеристического уравнения. Матрица, А и транспонированная к ней матрица, А удовлетворяет своему характеристическому уравнению D (A)=0. Но может оказаться, что существуют многочлены () степени меньше n, для которых также выполняется равенство (А)=(А)=0. Среди таких многочленов имеется единственный многочлен со старшим коэффициентом 1, имеющим наименьшую степень. Этот многочлен называется минимальным. Если минимальный многочлен матрицы не совпадает с характеристическим, то С=0 при любом выборе начального вектора. В этом случае АС0=0 и векторы С0, АС0, …, Аn-1C0 линейно зависимы.

На практике при использовании метода Крылова такая ситуация может возникнуть лишь при особых обстоятельствах.

Можно подсчитать, что при раскрытии характеристического многочлена матрицы с помощью метода Крылова потребуется 0,5(2п3+п2+п) операций умножения и деления.