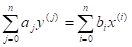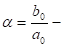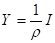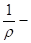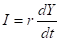Введение. 
Математические методы исследования обратных экономических динамических систем

В данной статье сформулирована обратные задачи экономических динамических систем[1]: акселератор и модель Кейнса.

Метод решения проиллюстрирован на статистическом материале по Северо-Кавказскому округу[6].

Для этой модели предложен метод решения обратной задачи, основанный на сведении обратной задачи к задаче квадратичного программирования.

Задачу квадратичного программирования предлагается решать инструментальными средствами: с помощью надстройки «Поиск решения» в среде MS Excel.

Цель проведённого исследования - разработать математические методы решения обратных задач экономических динамических систем и использовать полученные результаты для анализа и прогноза развития экономик Северо-Кавказского и Южного федеральных округов в целом и Карачаево-Черкесской республики, в частности.

Постановка задачи линейной динамической системы

Линейный динамический элементго порядка задаётся следующим дифференциальным уравнением[1]:

. (1).

На практике часто встречается элементы нулевого порядка: мультипликатор и акселератор.

Определение 1. [1] Мультипликатор-это линейное статическое звено, задаваемое уравнением:

или, (2).

где коэффициент усиления.

Валовые инвестиции, например, связаны с валовым внутренним продуктом (ВВП) следующим образом:

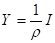
(3).

где доля валовых инвестиций в ВВП, а коэффициент усиления или мультипликатор, который показывает, насколько должен быть увеличен ВВП для увеличения валовых инвестиций на единицу.

Прямая задача: по заданным и определить .

В рамках модели (3) рассмотрим обратную задачу: по заданным и найти коэффициент усиления.

Подробнее остановимся на следующем звене — акселераторе.

Определение 2. 1] Акселератор — это дифференцирующее звено нулевого порядка, выход которого пропорционален скорости входа.

Инвестиции могут быть выражены через скорость изменения ВВП следующим образом:

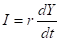
(4).

где валовый внутренний продукт;

валовые инвестиции;

коэффициент акселерации.

Коэффициент акселерации показывает прирост потребности в инвестициях при увеличении ВВП на единицу.

Прямая задача: по заданным в (4) коэффициента акселерации и изменениям найти инвестиции.

В этой статье в рамках модели (4) рассматривается другая задача [2]: по заданным модели в текущий момент времени и изменениям валового внутреннего продукта найти неизвестные коэффициенты акселерации, т. е. прирост потребности в инвестициях при увеличении ВВП на единицу.

Сформулированную задачу будем называть обратной задачей в рамках модели (4).

Постановка обратной задачи имеет смысл в силу того, что прямая задача поставлена корректно[3].

Действительно, данное уравнение является линейным с коэффициентом будем предполагать, что является непрерывной функцией на .

Тогда (4) имеет единственное решение, которое непрерывно зависит оти. Следовательно, задача (4) поставлено корректно, а значит, в силу (4) поставлена и обратная задача.