Дискретные модели линейных стационарных систем и стационарных случайных процессов

Рассмотрим линейную стационарную динамическую систему при действии возмущений, заданных в виде стационарных случайных процессов. Полагаем, что случайные процессы выражаются с помощью формирующих фильтров (2.7) через белый шум. Последовательно соединение исходной системы и формирующего фильтра образует эквивалентную систему.

Такая система может быть описана векторным дифференциальным уравнением.

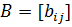
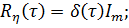
где x — n-мерный вектор состояния, — матрицы постоянных коэффициентов размеров и — mмерный гауссовский белый шум с нулевым средним и матричной корреляционной функциейединичная матрица. Начальные условия представляют собой гауссовский вектор — корреляционная матрица инезависимые случайные векторы.

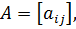
Дискретизация системы.

Для моделирования системы (2.34) на цифровой ЭВМ перейдем к дискретной модели. Выразим через матричный экспоненциал.

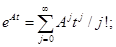
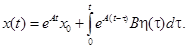
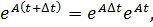
Используя свойство представим процесс и момент в следующем виде:

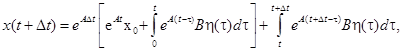
гдешаг дискретизации .

Соотношению (2.37) соответствует рекуррентное уравнение.

где.

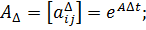
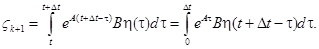
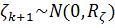
Векторы являются независимыми, гауссовскими, и не зависит от Корреляционная матрица имеет вид.

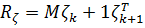
Представим в виде.

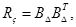
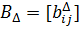
гдематрица порядкаранг.

Здесь матрица находится по с помощью алгоритмов (1.62)-(1.64) гл. 1. Тогда может быть выражен через равенством. Отсюда и из формулы (2.38) следует уравнение Уравнение (2.42) может использоваться для моделирования системы (2.34) на ЭВМ, а также для получения реализации стационарных случайных процессов, заданных уравнением формирующего фильтра вида (2.34). Моделирующий алгоритм, основанный на уравнении (2.42), не имеет методических ошибок. Алгоритм позволяет воспроизводить на ЭВМ случайные последовательности с заданными корреляционными функциями.

Корреляционные моменты. Определение начальных условий для компенсации переходных процессов.

Корреляционная матрица как следует из уравнения (2.42), определяется рекуррентным соотношением.

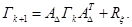
Примем далее, что матрица, А в системе (2.34) -Гурвицева, т. е. её собственные числа удовлетворяют условию.

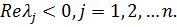
В силу (2.36) матричная корреляционная функция при равна.

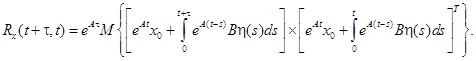
Отсюда, учитывая некоррелированность процесса и его независимость от, после взятия математического ожидания получаем формулу.

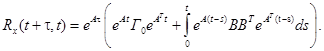
Здесь выражение в скобках равно корреляционной матрице процесса. При справедливо равенство.

.

После замены переменной интегрирования функция примет вид.

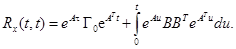
Для Гурвицевых матриц имеет последовательно равенства:

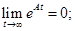
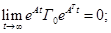
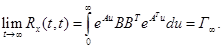
Эти равенства означают, что в системе (2.34) асимптотически устанавливаются стационарные случайные процессы с нулевым средним и корреляционной матрицей Матрица находится предельным переходом в уравнении (2.43) при Переходя в формуле (2.43) к пределу, получаем линейно алгебраическое уравнение.

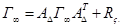
Матрицу можно также найти из соотношения (2.10). Если положить в (2.43), то из формулы (2.44) получаем равенства:

.

Это означает, что корреляционные свойства процесса не изменяются с течением времени. В системе (2.34) отсутствуют переходные процессы, а стационарный процесс устанавливается, начиная с момента, поэтому для устранения переходных процессов в уравнении (2.42) необходимо положить.

Матрица находится из матричной системы дифференциальных уравнений интегрированием выражения (2.45) на промежутке при начальной условии. После интегрирования получаем. Для приближенных вычислений модно пользоваться формулой (2.35), ограничиваясь конечным числом членов:

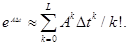
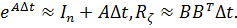
Рассмотрим, какой вид имеет уравнение (2.42) при малом шаге В (2.46) отбросим члены второго и высшего порядка малости. Тогда получим После подстановки этих выражений в формулу (2ю42) следует приближенное равенство.

.

При стремлении к нулю получаем.

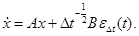
Это выражение соответствует формуле (2.14), выведенной ранее другим способом.

Моделирующий алгоритм.

Алгоритм цифрового моделирования включает следующие операции [93]:

• 1. Модель динамической системы или формулирующего фильтра приводится к виду (2.34)
• 2. Вычисляется n-мерная матрица Для этого n раз интегрируется система

гдеj-й столбец единичной матрицымерный вектор. Решение системы (2.48) в момент даетй столбец матрицы .

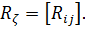
3. Вычисляется матрица В соответствии с формулой (2.40) её элементы равны.

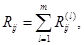
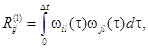
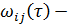
где компонент матрицы.

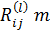
Для определения раз интегрируется системы дифференциальных уравнений:

.

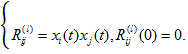
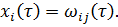
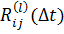
Здесьй столбец матрицы B, В результате суммирования величин по l находятся элементы симметрической матрицы .

• 4. По рекуррентному алгоритму (2.43) вычисляется корреляционная матрица. В качестве можно принять любую неотрицательно определенную симметрическую матрицу, например нулевую. Выбор оказывает влияние только на время переходного процесса. Итеративный процесс (2.43) заканчивается, когда матрица примет с заданной точностью установившееся значение.
• 5. С помощью алгоритмов (1.62)-(1.64) вычисляется матрица размера определяемая соотношением (2.41).
• 6. Разыгрывается вектор начальных условий; или при моделировании стационарных процессов и установившихся режимов движения (2.34). Для этого также применяются алгоритмы (1.62)-(1.64). Разыгрыванием начального условия заканчивается подготовительный этап вычислений.
• 7. Выполняется цифровое моделирование динамической системы или стационарного случайного процесса по формуле (2.42).

Сравнивая алгоритм (2.42) с методами моделирования стационарных процессов, рассмотренными в п. 2.1, можно отметить следующее: алгоритм не содержит методических ошибок, т. е. статические характеристики генерируемой последовательности и выборки с шагом из реализации процесса с непрерывным временем совпадают; подготовительный этап не содержит операций, выполняемых только аналитическими методами, — все операции выполняются численно с использованием стандартных процедур; при моделировании отсутствуют переходные нестационарные процессы; исходными данными являются не спектральные и корреляционные характеристики, а матрицы A, B марковского процесса (2.34), определение которых, как правило, не вызывает трудностей. Причем для векторных процессов задание пары A, B на практике часто являются более естественным способом описания, чем матричные корреляционные или спектральные характеристики. Данный метод может иметь преимущества перед известными для процессов со спектрами относительно высокого порядка. векторный линейный стохастический корреляционный.

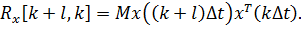
С использованием дискретной модели (2.42) могут решаться задачи статического анализа линейных стационарных систем. Дисперсии и корреляционные моменты фазовых координат системы (2.34) являются компонентами матрицы или матрицы в установившемся режиме. Эти матрицы находим из уравнений (2.43) и (2.44). Рассмотрим матрицу Её элементы представляют собой корреляционные и взаимные корреляционные функции. Как следует из уравнения (2.42),.

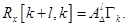
В установившемся режиме для стационарных процессов соотношение (2.51) принимает вид.

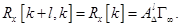
При большом n в выражении (2.34) применение формул (2.43), (2.44) и (2.51), (2.52) позволяет значительно сократить объем промежуточных вычислений по сравнению с известными методами анализа непрерывных систем [112, 124].

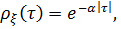
Пример 2.1. Частным случаем системы (2.34) является марковский гауссовский стационарный процесс первого порядка. Его нормированная корреляционная функция равна уравнение (2.34) имеет вид.

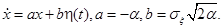
Формулы (2.38)-(2.41) дают для коэффициентов дискретной модели (2.42) следующие выражения:

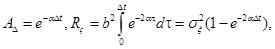
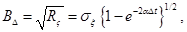
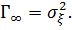
Модель (2.42) примет вид.

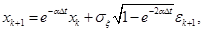
Пример 2.2. Рассмотрим стационарный случайный процесс, имеющий спектры второго порядка.

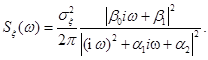
Используя соотношения (2.8) и (2.9), представим его в виде компоненты марковского процесса.

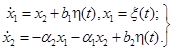
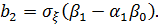
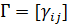
где Для исключения переходных процессов в уравнении (2.56) необходимо, чтобы начальное условие моделировалось в виде двумерного гауссовского вектора где корреляционная матрица находится из (2.10) или (2.44). Решение уравнения (2.10) для данной системы дает следующие значения :

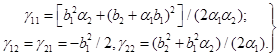
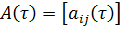
Для построения алгоритма (2.42) найдем матрицы и. Дифференциальные уравнения для определения имеют вид.

Первый столбец матрицы получаем, решая эту систему при начальных условиях второйпри начальных условиях В результате имеем:

а) при >0, ,.

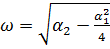
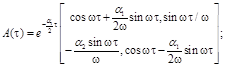
б) при.

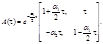
Из формул (2.40) и (2.49) следует, что матрица равна.

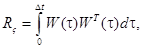
где решение системы (2.58) с начальными условиями. В силу линейности системы (2.58) имеем.

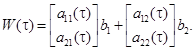
Отсюда получает формулы для элементов :

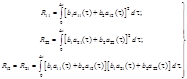
Матрицу определяем из соотношения (2.41) с помощью формул (1.62)-(1.64). Элементы равны :

,.

.

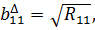
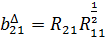
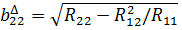
В результате окончательно получаем.

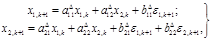
где.

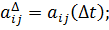
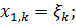
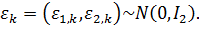
Приведенные в данном примере формулы позволяют моделировать случайные процессы с различными типами корреляционных функций, встречающиеся в практике.

Пример 2.3. Рассматривалась система стабилизации высоты полета, заданная системой дифференциальных уравнений.

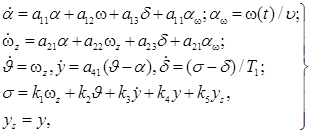
где вектор состояния системы; возмущение (турбулентность атмосферы), стационарный случайный процесс с нулевым средним, корреляционной функцией [43];

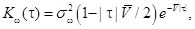
и спектральной плотностью.

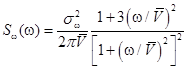
вида (2.55). Здесь дисперсия скорости ветра; масштаб турбулентности.

Система (2.64) дополняется уравнением (2.56) формирующего фильтра для процесса и приводится к виду (2.34). С использованием алгоритма (2.48)-(2.50) на ЭВМ строилась дискретная модель соответствующая системе дифференциальных уравнений (2.64). Здесь вторая компонента в уравнении (2.56); матрицы порядка.

С помощью дискретной модели (2.67) выполнялось моделирование системы стабилизации (2.64) на ЭВМ. Дискретная модель (2.67) использовалась при полунатурном моделировании, а также для обработки реализации случайных процессов при вычислении эффективных и квазиэффективных оценок их характеристик. На основе рекуррентных алгоритмов (2.43), (2.44), (2.51), (2.52) определялись корреляционные функции процессов в системе стабилизации.

Нормированные корреляционные функции процессов и результаты их аппроксимации типовыми функциями показаны на рис. 2.1. График аппроксимировался функциями при аппроксимации функциями получили соответственно.

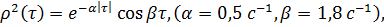
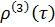
Аппроксимацию функцией следует применять тогда, когда учитывается свойство дифференцируемости процессов. Сравнение с методом непрерывного анализа подтвердило эффективность рекуррентных алгоритмов. Так применение рекуррентных алгоритмов позволило на порядок сократить время счета на ЭВМ при вычислении корреляционных функций.