Метод осреднения Ван-дер-Поля

Рассмотрим один из вариантов методов осреднения — метод Ван-дерПоля, или метод медленно меняющихся коэффициентов. Этот подход был предложен Ван-дср-Полем для приближенного решения уравнения колебаний с малым возмущением вида.

где 0 < е 1 — малый параметр.

Метод медленно меняющихся коэффициентов основан на методе вариации произвольных постоянных. В случае когда правая часть уравнения (4.40) имеет вид.

уравнение (4.40) называется уравнением Ван-дер-Поля.

Представим решение уравнения (4.40) в виде функции, являющейся решением обычного уравнения колебаний, т. е. уравнения (4.40) без правой части:

где а = a (t) и (р = <�р (Р) являются, соответственно, медленно меняющимися амплитудой и фазой. Эти величины находят из решения системы двух обыкновенных дифференциальных уравнений. Выведем их, для чего уравнение (4.40) представим в виде.

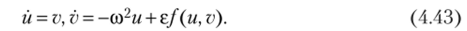
В случае е = 0 имеем.

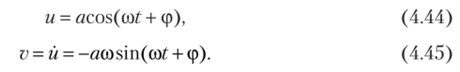
Будем искать решение в виде (4.44), (4.45), для чего продифференцируем уравнение (4.42) и сравним его с выражением для v (t). После этого получим.

Далее продифференцируем выражение (4.45) по t и подставим в уравнение (4.40), имеем.

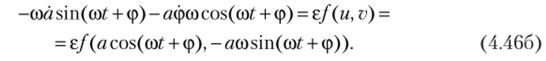
Разрешая систему (4.46а), (4.466) относительно а и ф, получаем.

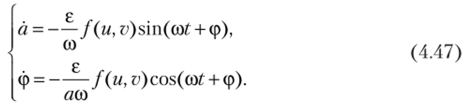
Отсюда ясно, что а и (р являются медленно меняющимися переменными, так как правые части системы пропорциональны малому параметру в.

Заметим, что правые части системы (4.47) периодические по t с периодом 2п/со. Их можно разложить в ряды Фурье по t. Тогда получим.

Здесь f*j, g^k — коэффициенты разложения.

В этой системе Ван-дер-Полем был предложен следующий способ осреднения по времени: опустить осциллирующие члены, т. е. оставить лишь нулевые гармоники. В этом случае система принимает вид.

где А (а) = -/₀¹ (а), В (а) = -g$(a), или.

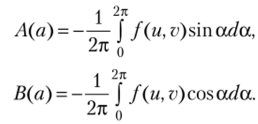
Проиллюстрируем изложенный метод на каноническом примере — приближенном решении уравнения Ван-дер-Поля.

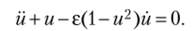
Переходим к новым переменным и получаем систему.

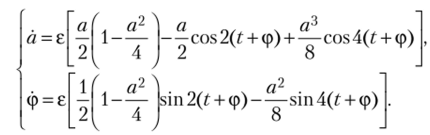
Оставим в ней только нулевые гармоники. Соответственно, система приобретает вид.

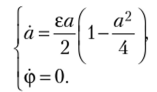
Умножая первое уравнение на 2а, получим 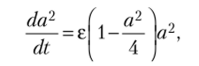или.

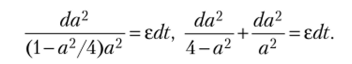
Интегрируя полученное уравнение при начальном условии а (0) = а₀, получим.

Окончательное решение запишем в виде

Приведем пример приближенного решения уравнения Дюффинга:

с помощью метода Ван-дер-Поля.

Решение, как и в предыдущем случае, ищем в виде.

полагая, что а и ф зависят от времени. Дифференцируя первое уравнение для и по t и сравнивая сто со вторым, для v получим.

Дифференцирование уравнения для v по t и последующая подстановка результатов в исходное уравнение (4.49) дают.

Разрешая два последних полученных дифференциальных уравнения относительно а и ф, получим.

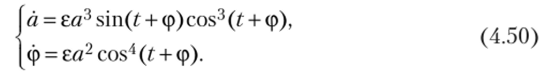
Воспользовавшись тождествами.

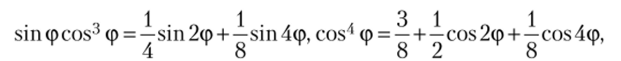
перепишем полученную систему в виде.

где введено обозначение, а = t + ф.

В соответствии с методом Ван-дер-Поля получим, оставляя лишь нулевые гармоники:

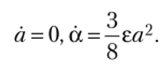
Решая эту систему относительно а и а, находим зависимость от времени амплитуды и фазы:

где а_{) = я (0), а₍₎ = а (0) — начальные условия. Окончательное решение исходного уравнения будет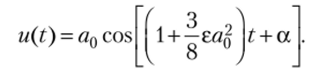

Получим тот же результат с помощью другого метода осреднения. Усредняя правые и левые части уравнений (4.50) по интервалу периодичности функций в правых частях [0; л], получаем следующие выражения:

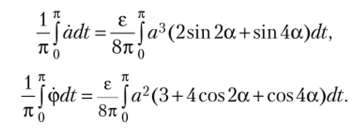
Вследствие медленного изменения функций а и ср на [0; л] будем полагать, что они на этом интервале постоянны. Тогда.

Проведем замену переменных, а = t + (р, тогда do. = dt и, соответственно, уравнение для амплитуды имеет вид.

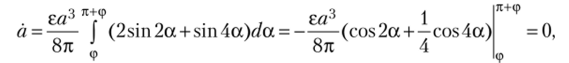
а для фазы.

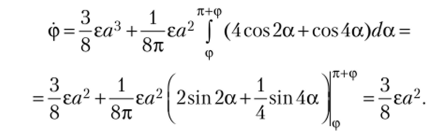
Отметим, что последний способ осреднения по периоду представляется более обоснованным, нежели метод Ван-дер-Поля.