Применение встроенной функции pdepe для решения системы уравнений в частных производных параболического типа

Общий вид системы относительно неизвестной вектор-функции может быть представлен следующим уравнением:

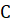
. (2.43).

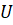
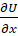
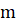
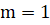
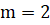
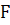
Здесь матрица, векторы и зависят от переменных, ,,. Матрица является диагональной, по крайней мере, один элемент ее должен быть ненулевым. Для уравнения теплопроводности вектор определяет поток, а вектор описывает источники.

Введение

параметра позволяет решать одномерные задачи для радиальной координаты в цилиндрической или полярной () а также сферической () системах координат.

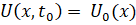
Начальные условия определяются для вектора неизвестных:

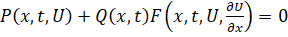
. (2.44).

Краевые условия задаются в следующем виде:

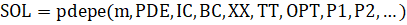
. (2.45).

Обращение к функции решения системы уравнений в частных производных имеет вид:

.

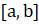
Здесь параметр определяет систему координат: 0 отвечает декартовым координатам, 1 — цилиндрическим, 2 — сферическим.

Вычисление правой части рассматриваемой системы производится в функции PDE, данные о начальных условиях берутся из функции IC, а краевые условия задаются функцией ВС.

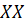
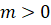
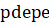
Сетка по координате на интервале должна содержать не менее трех узлов и задается массивом, содержащим узлы в порядке возрастания координаты. Лучше использовать более мелкий шаг между узлами в тех областях, где решение меняется значительно, и более крупный шаг в местах плавного изменения решения. Для (цилиндрические или сферические координаты) не обязательно сгущать сетку в окрестности особой точки, и при значение не может быть отрицательным.

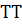
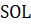
Для интегрирования задачи по времени в функции используются команды для решения задачи Коши, а применяемый метод и шаг интегрирования выбираются функцией. Массивом определяется набор временных слоев, в которых будут запомнены решения, таких слоев должно быть не менее трех.

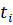
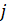
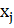
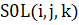
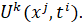
Решение выводится в трехмерный массив, причем первый индекс () отвечает временному слою, второй индекс () определяет номер узла, а третий индекс дает номер компоненты вектора решения. Таким образом, элемент дает значение решения.

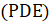
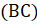
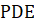
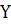
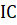
Рассмотрим заголовки функций вычисления правой части и задания начальных () и краевых условий. Входными параметрами для функции вычисления правой части с именем являются точка отрезка, вектор значений в этой точке и параметры задачи, и т. д. Выходные данные представлены диагональной матрицей и векторами, :

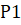
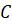
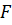
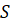
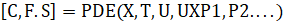
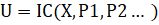
Начальные условия даются функцией:

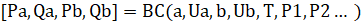
Краевые условия обрабатываются функцией:

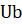
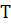
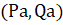
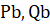
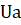
Здесь векторы и дают значения вектора на разных концах интервала , — время, а выходные параметры представлены векторами на левом и правом () концах интервала.

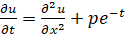
Рассмотрим применение команды для решения уравнения теплопроводности с источником (- параметр):

.

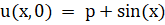
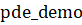
Начальное распределение температуры есть и заданы следующие краевые условия: Дирихле (первого рода) на левом конце и Неймана (второго рода) на правом конце.

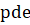
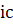
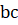
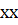
Создадим m-функцию, в которой будут использованы операторы подготовки и вычисления решения, а также вспомогательные функции вычисления правой части, задания начальных () и краевых () условий. Указывая имена этих подфункций в качестве параметров команды, используем префикс @.

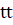
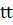
Обозначения переменных практически повторяют использованные для описания параметров команды. Концы отрезка изменения переменной есть и , — параметр, число ячеек на отрезке —, переменная определяет узлы сетки по, а переменная задает временные слои.

Пример реализации m-файла приведен в приложении В.

На рисунке 2.5 приведены графики, полученные в результате запуска функции .

График справа дает распределение температуры на последнем из рассчитанных временных слоев, сплошной линией представлено имеющееся для данной задачи точное решение, а кружками — результаты расчета при помощи функции. Видно, что при остывании стержня сохраняется форма начального распределения.

Уравнение решалось численно с помощью разработанной программы при значениях параметров:

a=0;

b=3*pi/2;

n=16;

p=1;

tt=0:.2:3;

C = 1;

F = DuDx;

S = -p*exp (-t);

u0 = p+sin (x);

Pa = ua-p*exp (-t);

Qa = 0;

Pb = 0;

Qb = 1;

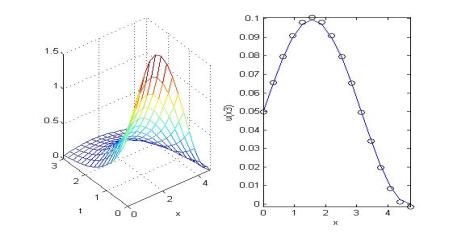
Рисунок 2.5 Решение уравнения теплопроводности.