Классификация автоматов. 
Разработка недетерминированных программных систем на основе вероятных автоматов

Используемые на практике автоматы принято делить на 2 класса — это автоматы Мили и автоматы Мура, названные так по имени американских экспертов, которые в первый раз начали их изучать. Функционирование автоматов строго подчиняется конкретным законам законы — функционирования автоматов. Законы функционирования автоматов описываются системами уравнений. Рассмотрим каждый из автоматов подробней.

Законы функционирования автомата Мили описываются последующей системой уравнений, представленные в таблице 2.

Таблица 2. Автомат Мили.

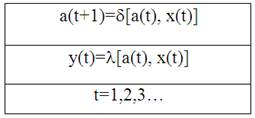
Функциональная схема автомата Мили представлена на рисунке 1.

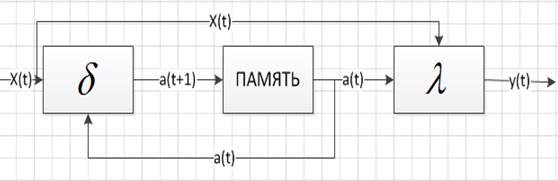
Рисунок 1. Схема автомата Мили Характерной особенностью автоматов Мили считается то, что их выходные сигналы находятся в зависимости, как от состояния автомата, так и от значения входного сигнала.

Законы функционирования автомата Мура описываются последующей системой уравнений, представленные в таблице 3.

Таблица 3. Автомат Мура.

Функциональная схема автомата Мили представлена на рисунке 2.

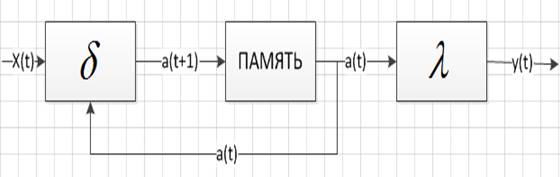
Рисунок 2. Схема автомата Мура.

Способы задания автоматов

Чтобы задать конечный автомат S, нужно описать все элементы множества S={А, Х, Y,, }. То есть нужно описать входной, выходной алфавиты и алфавит состояний, а также функции переходов и выходов. При этом среди большого количества А={а₀, а₁,…, а_n} нужно отметить начальное состояния а₀, в котором автомат располагаться в момент времени t=0. Существует некоторое количество способов задания работы автомата, однако наиболее часто используются табличный и графический.

Табличный способ. При табличном способе задания автомат Мили описывается 2-мя таблицами: таблицей переходов и таблицей выходов (таблицы 4,5).

Таблица 4. Таблица переходов.

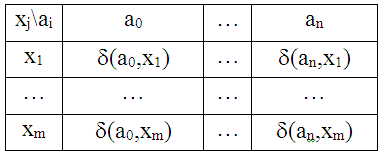
Таблица 5. Таблица выходов.

Строки данных таблиц соответствуют входным сигналам х (t), а столбцы — состояниям. На пересечении столбца а_i и строки х_j в таблице переходов ставится состояние а_s=[а_i, х_j], в которые автомат перейдет из состояния а_i под действием сигнала х_j; а в таблице выходов — соответствующий данному переходу выходной сигнал y_g=[а_i, х_j]. Время от времени автомат Мили задают совмещенной таблицей переходов и выходов, она в некоторых вариантах более удобна (таблица 6).

Таблица 6. Совмещенная таблица переходов и выходов автомата Мили.

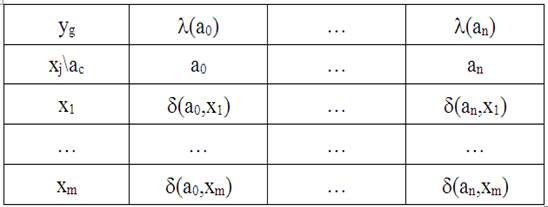
Задание таблиц переходов и выходов вполне описывает работу конечного автомата, поскольку задаются не только сами функции переходов и выходов, но еще и все 3 алфавита: входной, выходной и алфавит состояний. Так как в автомате Мура выходной сигнал однозначно определяется состоянием автомата, то для его задания требуется лишь 1 таблица, которая именуется отмеченной таблицей переходов автомата Мура (таблица 7).

Таблица 7. Отмеченная таблица переходов автомата Мура.

Примеры табличного задания автоматов Мили и Мура (таблицы 8,9).

Таблица 8. Автомат Мура.

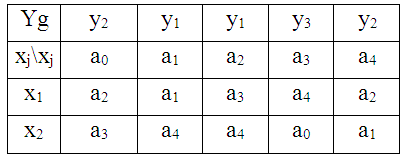
Таблица 9. Автомат Мили.

По этим таблицам можно найти реакцию автомата на любое входное слово: для автомата Мура в таблице 10, для автомата Мили в таблице 11.

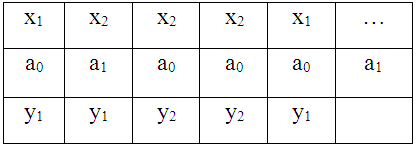
Таблица 10. Реакция автомата Мура.

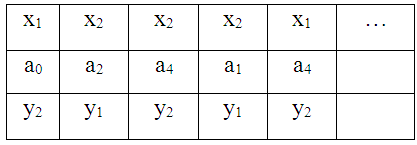
Таблица 11. Реакция автомата Мили.

Графический способ. При графическом способе задание автомата осуществляется с помощью графа. Граф для автоматов Мили и Мура представлен на рисунке 3 и 4 соответственно.

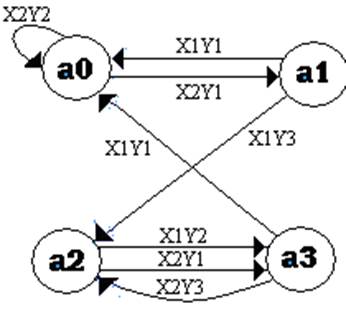
Рисунок 3. Граф для автомата Мили.

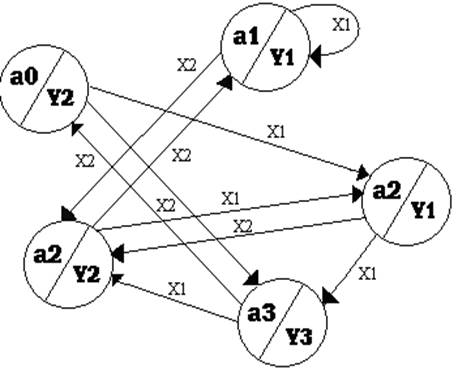
Рисунок 4. Граф для автомата Мура Данный способ базируется на применении ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги — переходам между ними. 2 вершины графа а_i и а_s объединяются дугой, направленной от а_i к а_s, если в автомате имеется переход из а_i в а_s, то есть а_s=(а_i, х_j).