Системы линейных уравнений и неравенств

1. Системы линейных уравнений.

Рассмотрим систему из n линейных уравнений с n неизвестными.

^a11^x1 + ***^a1n^xn = ^b1, (3.12).

^an1^X1 + ***^ann^xn = ^bn.

где Xi — неизвестные; ajj — коэффициенты системы; bi — свободные члены.

Система чисел (x₁, x₂,…, x_n) называется решением системы уравнений (3.12), если эти числа при подстановке в систему (3.12) превращают его в тождество.

Если система (3.12):

• а) не имеет ни одного решения, то она называется несовместной;
• б) имеет решение — совместной;
• в) если совместная система имеет бесконечное множество решений, то она называется неопределенной;
• г) если совместная система имеет единственное решение, то она называется определенной.

Пусть векторы aj — столбцы матрицы А, т. е. эту матрицу можно представить в виде, А = (a₁, а₂,., а_п).

Введем определители: |А| = |a₁, a₂,…, a_n| и |Ak| =|a₁, a₂,…, bk, a_n|, т. е. столбец а^ заменяется на столбец свободных членов bk.

Правило Крамера. Если определитель системы (3.12) отличен от нуля, т. е. |А| ^ 0, то система уравнений имеет единственное решение, вычисляемое по формуле.

Xk = ^ (k = 1, 2,…, n). (3.13).

ПРИМЕР 1.

Решить систему линейных уравнений методом Крамера:

x + 2y + z = 8 2x + y + z = 7 3x + 2y + 2z = 13.

Решение Вычислим определители:

• 8. (1.2 — 1. 2) —
• — 2. (7. 2 -1. 13) +

+ 1. (2. 2 — 3. 1) = - 1.

• 1. (7.2 — 1. 13) —
• — 8. (2. 2 -1. 3) +

+ 1. (2. 13 — 3. 7) = - 2.

• 1. (1.13 — 7. 2) —
• — 2. (13. 2 — 3. 7) +

+ 8. (2. 2 — 3. 1) = - 3.

По правилу Крамера:

Ответ: х — 1, у — 2, z — 3.

Метод Гаусса.

Представим метод Г аусса решения системы линейных уравнений на примере трех уравнений с тремя неизвестными х, y, z.

Метод Гаусса заключается в последовательном исключении неизвестных и приведении системы к диагональному виду:

х + с12 у + с 13 z = di.

у + С23 z = d2 (3.15).

z = d3.

Неизвестные x, y, z из полученной системы (3.15) последовательно вычисляются ''обратным ходом «.

Алгоритм метода Г аусса. 1-ый шаг.

Допустим, что а₁₁ * 0.

Делим тогда 1-ое уравнение в (3.14) на а₁₁ и получаем:

^х + ^(a12/^a11 ⁾ У + ^(a13/^a11 ^{) z} = ^d1^/a11.

Переобозначим коэффициенты:

х + с12 у + 013z = d1 (3.16).

2-ой шаг.

Умножаем уравнение (3.16) на (-а₂₁) и складываем со вторым уравнением (3.14).

Получаем:

^(-а21 + ^а21 ^)х + У^{(- c}12 ^a21 + ^a22 ⁾ + ^{z (- c}13 ^a21 + ^a23 ⁾ = ^b2 ^— d1 ^a21.

Разделим это уравнение на (- c₁₂ a₂₁ + a₂₂) и, переобозначив коэффициенты, получаем у + c23 z = d2 (3.18).

3-ий шаг.

Умножаем уравнение (3.16) на (-а₃₁) и складываем с третьим уравнением в (3.14):

^(-а31 + ^а31 ^)х + у (- С12 ^a31 + ^a32) + ^{z (} — C13 ^a3l + ^a33) = ^b3 ^— d1 ^a3i.

Переобозначим коэффициенты в предыдущем уравнении:

^С32 у + ^c33 ^z = ^d3.

В итоге после первого цикла из 3-х шагов система уравнений принимает вид:

X + с12 У + с 13 Z У + С23 Z С32 У + С33 Z.

= d1 = ^d2 = d3 (3.19).

4-ый шаг.

Умножаем второе уравнение в (3.19) на (-с₃₂) и складываем с третьим уравнением в этой системе:

^(-с32 + ^с32⁾ У + ^{z (-с}32 ^с23 + ^с33⁾ = ^d3 ^— d2 ^С32.

Откуда:

^z = ^(d3 ^— d2 ^С32^{) / (с}33 ^-с32 ^с23 ⁾ = ^d3.

В итоге получаем треугольную систему уравнений:

X + с12 у + с 13 Z = d1.

У + С23 Z = d2.

z = d3 (3.20).

Из которой неизвестные х, у, z получаем «обратным ходом»:

Z = (d3 — d2 С32) / (с33 -с32 с23).

У = d2 — + С23 Z.

X = d1 — с 12 У — (3.21).

ПРИМЕР 2.

Решить систему линейных уравнений методом Г аусса: 1.

2х + 4у + 2 z = 16 2х + у + z = 7 3х + 2у + 2z = 13.

Решение.

1 -ый шаг.

_Разделим первое уравнение на (2):

х+2у + z = 8.

2-ой шаг.

Умножим первое уравнение на (-2) и сложим со вторым уравнением:

• (-2+2)х +(-4 +1)у + (-2+1) = -16+7 = -9.
• 3-ий шаг.

Умножим первое уравнение на (-3) и сложим с третьим:

(-3 +3)х +(-6 +2)у + (-3+2) = -24+13 = -11.

После первого цикла получаем х + 2у + z = 8 у + z/3 = 3.

• 4у + z = 11
• 4-ый шаг.

Умножаем второе уравнение на (-4) и складываем с третьим (-4 +4)у + z (-4/3 + 1) = -12 = 11 В итоге получаем:

— z/3 = -1, z = 3.

Треугольная система уравнений принимает вид:

х + 2у + z = 8 у + z/3 = 3.

z = 3.

В результате обратного хода получаем:

у = 3 — 3/3 = 2, х = 8 — 2(2).

Ответ: х = 1, у = 2, z = 3.

2. Системы линейных неравенств.

Рассмотрим систему n линейных неравенств:

^a11 * ^х1 + ^a12 * ^х2 + — + ^a1n * ^xn < ^b1^;

^ ^a21 * ^х1 + ^a22 * ^х2 + — + ^a2n * ^xn < ^b2^; (3.22).

a_m1 * х1 + a_m2 * х2 + — + a_mn * хп < bm;

где а! j, bi, Cj — заданные постоянные величины, х = (х₁, х₂, — х_п) — векторстрока переменных.

Если система неравенств (3.22) совместна, она определяет некоторое множество, совокупность точек которого образует выпуклый многогранник.

Построить этот многогранник сравнительно просто, если задача содержит не более двухтрех свободных переменных, т. е. n-r < 2- 3, где n — число переменных, г — ранг матрицы А.

В качестве примера построим выпуклый многонранник, определяемый системой неравенств:

а_пх + а12 У < b1 (3.23).

< а21х + а22 У 0; У > 0.

Каждое из неравенств (3.23) системы ограничений геометрически определяет полуплоскость, ограниченную прямыми.

an х + a12 У = b1,.

a21 х + a22 У = b2, (3.24).

х = 0, У = 0.

В том случае, если система неравенств (3.23) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Каждая полуплоскость образует выпуклое множество, тогда множество их пересечений и образует выпуклый многогранник.

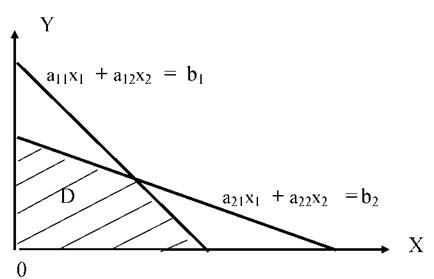
Рис. 3.5 Выпуклый многогранник D, заданный системой неравенств (3.23)

ПРИМЕР 3.

Построить многогранник D, заданный системой неравенств:

3х + 2 у < 6 2х + 3у 0; у > 0.

Решение Неравенства x > 0; у > 0 задают 1-ую четверть координатной плоскости Построим прямую: 3x + 2у = 6.

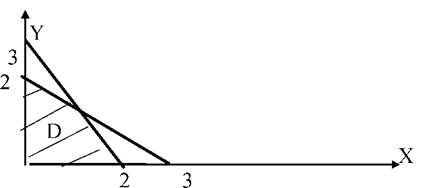
При х = 0: 2у = 6; у = 3; при у = 0: 3х = 6, х = 2. Следовательно, прямая проходит через точки (0, 3) и (2, 0). Построим прямую: 2x + 3у = 6.

При х = 0: 3у = 6, у = 2; при у = 0: 2х = 6, х = 3. Следовательно, прямая проходит через точки (0, 2) и (3, 0).

Область D определяется пересечением полуплоскостей:

3x + 2у < 6 2x + 3у < 6.

ЗАДАНИЕ.

1). Решить систему линейных уравнений методом Гаусса и формуле Крамера:

по.

2х + 4у + 6 z = 14 х + 2у + 3z = 7 3х + у + z = 8.

Ответ: х = 2, у = 1, z.

• 2). Решить систему линейных уравнений методом Гаусса и формуле Крамера:
• 2х + 3у + z = 7 2х + у — z = 1 4х + 2у — z = 4

Ответ: х = 1, у = 1, z = 2.

• 3). Построить многогранник, заданный системой неравенств:
• 2х + 4у < 8 3х + 2у 0; у > 0.
• 4). Построить многогранник, заданный системой неравенств:
• 2х + 5у < 10 2х + 2у 0; у > 0.
• 5). Построить многогранник, заданный системой неравенств:
• 2х + 5у < 10 5х + 2у < 6 5х + 5у 0; у > 0.