Округление чисел. 
Погрешность округления

При выполнении вычислений часто возникает необходимость в округлении чисел, т. е. в замене их числами с меньшим количеством значащих цифр.

Существуют три способа округления чисел:

Округление с недостатком до k-й значащей цифры состоит в отбрасывании всех цифр, начиная с (k+1)-й.

Округление с избытком отличается от округления с недостатком тем, что последняя сохраняемая цифра увеличивается на единицу.

Округление с наименьшей погрешностью отличается от округления с избытком тем, что увеличение на единицу последней сохраняемой цифры производится лишь в том случае, когда первая из отбрасываемых цифр больше 4.

Исключение: если округление с наименьшей погрешностью сводится к отбрасыванию только одной цифры 5, то последняя сохраняемая цифра не изменяется если она четная, и увеличивается на 1, если она нечетная.

Из вышеуказанных правил округления приближенных чисел следует, что погрешность, вызываемая округлением с наименьшей погрешностью, не превышает половины единицы последнего сохраняемого разряда, а при округлении с недостатком или с избытком погрешность может быть и больше половины единицы последнего сохраняемого разряда, но не более целой единицы этого разряда.

Рассмотрим это на следующих примерах.

1. Погрешность суммы. Пусть x — некоторое приближение величины а, у — некоторое приближение величины b. Пусть х и у — абсолютные погрешности соответствующих приближений х и у. Найдем границу абсолютной погрешности h_a+b суммы х+у, являющейся приближением суммы а+b.

Имеем.

a = x + х,

b = y + y.

Сложим эти два равенства, получим.

a + b = x + y + х + y.

Очевидно, что погрешность суммы приближений x и у равна сумме погрешностей слагаемых, т. е.

(x + y) = x + y

Известно, что модуль суммы меньше или равен сумме модулей слагаемых. Поэтому.

(x + y) = x + y x + y

Отсюда следует, что абсолютная погрешность суммы приближений не превышает суммы абсолютных погрешностей слагаемых. Следовательно, за границу абсолютной погрешности суммы можно принять сумму границ абсолютных погрешностей слагаемых.

Обозначив границу абсолютной погрешности величины а через h_a, а величины b через h_b будем иметь.

h_a+b = h_a + h_b

2. Погрешность разности. Пусть х и у — погрешности приближений x и у соответственно величин a и b.

Тогда.

a = x + х,

b = y + y.

Вычтем из первого равенства второе, получим.

a — b = (x — y) + (x — y)

Очевидно, что погрешность разности приближений равна разности погрешностей уменьшаемого и вычитаемого, т. е.

(x — y) = x — y),.

или.

(x — y) = x + (-y)

А тогда, рассуждая так же, как в случае сложения, будем иметь.

(x — y) = x + (-y) x + y

Отсюда следует, что абсолютная погрешность разности не превышает суммы абсолютных погрешностей уменьшаемого и вычитаемого.

За границу абсолютной погрешности разности можно принять сумму границ абсолютных погрешностей уменьшаемого и вычитаемого. Таким образом.

h_a-b = h_a + h_b (9)

Из формулы (9) следует, что граница абсолютной погрешности разности не может быть меньше границы абсолютной погрешности каждого приближения. Отсюда вытекает правило вычитания приближений, применяемое иногда при вычислениях.

При вычитании чисел, являющихся приближениями некоторых величин, в результате следует оставить столько цифр после запятой, сколько их имеет приближение с наименьшим числом цифр после запятой.

3. Погрешность произведения. Рассмотрим произведение чисел х и у, являющихся приближениями величин a и b. Обозначим через x погрешность приближения х, а через у — погрешность приближения у,.

Имеем.

a = x + х,

b = y + y.

Перемножив эти два равенства, получим.

Абсолютная погрешность произведения ху равна.

И поэтому.

Разделив обе части полученного неравенства на ху, получим.

Учитывая, что модуль произведения равен произведению модулей сомножителей, будем иметь.

Здесь левая часть неравенства представляет собой относительную погрешность произведения ху, — относительную погрешность приближения х, а — относительную погрешность приближения у. Следовательно, отбрасывая здесь малую величину, получим неравенство.

Таким образом, относительная погрешность произведения приближений не превышает суммы относительных погрешностей сомножителей. Отсюда следует, что сумма границ относительных погрешностей сомножителей является границей относительной погрешности произведения, т. е.

E_ab = E_a + E_b (10).

Из формулы (10) следует, что граница относительной погрешности произведения не может быть меньше границы относительной погрешности наименее точного из сомножителей. Поэтому здесь, как и в предыдущих действиях, не имеет смысла сохранять в сомножителях излишнее количество значащих цифр.

Иногда при вычислениях для сокращения объема работы полезно руководствоваться следующим правилом: При умножении приближений с различным числом значащих цифр в результате следует сохранить столько значащих цифр, сколько их имеет приближение с наименьшим числом значащих цифр.

4. Погрешность частного. Если x — приближение величины а, погрешность которого x, а у — приближение величины b с погрешностью y, то.

Вычислим сначала абсолютную погрешность частного:

а затем относительную погрешность:

Принимая во внимание, что y мало по сравнению с y, абсолютную величину дроби можно считать равной единице. Тогда.

из последней формулы вытекает, что относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. Следовательно, можно считать, что граница относительной погрешности частного равна сумме границ относительных погрешностей делимого и делителя, т. е.

5. Погрешность степени и корня. 1) Пусть u = aⁿ, где n — натуральное число, и пусть, а х. Тогда, если E_a — граница относительной погрешности приближения x величины a, то.

и поэтому.

Таким образом, граница относительной погрешности степени равна произведению границы относительной погрешности основания на показатель степени, т. е.

E_u = n E_a (11).

2) Пусть, где n — натуральное число, и пусть ах.

По формуле (11).

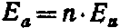
и, следовательно,.

погрешность вычитаемый вычисление Таким образом, граница относительной погрешности корня n-й степени в n раз меньше границы относительной погрешности подкоренного числа.

6. Обратная задача приближенных вычислений. В прямой задаче требуется найти приближенное значение функции u=f (х, у,…, n) по данным приближенным значениям аргументов.

и границу погрешности h_a, которая выражается через погрешности аргументов некоторой функции.

h_u = (h_x, h_y, …, h_z) (12)

На практике нередко приходится решать и обратную задачу, в которой требуется узнать, с какой точностью должны быть заданы значения аргументов х, у, …, z, чтобы вычислить соответствующие значения функции u = f (х, у, …, z) с наперед заданной точностью h_u.

Таким образом, при решении обратной задачи искомыми являются границы погрешностей аргументов, связанные с заданной границей погрешности функции h_u уравнением (12), и решение обратной задачи сводится к составлению и решению уравнения h_u = (h_x, h_y, …, h_z) относительно h_x, h_y, …, h_z. Такое уравнение или имеет бесконечное множество решений, или совсем не имеет решений. Задача считается решенной, если найдено хотя бы одно решение такого уравнения.

Для решения обратной задачи, которая часто бывает неопределенной, приходится вводить добавочные условия об отношениях искомых погрешностей, например считать их равными и тем самым сводить задачу к уравнению с одним неизвестным.