Теория вероятностей и математическая статистика

Оборудование после k лет может оказаться в одном из трех состояний: Q1 — оборудование вполне работоспособно и требует лишь небольшого текущего ремонта; Q2 — требуется серьезный капитальный ремонт; Q3 — дальнейшая эксплуатация оборудования невозможна. Вероятности этих состояний 0,2; 0,6; 0,2. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно М (х… Читать ещё >
Теория вероятностей и математическая статистика (реферат, курсовая, диплом, контрольная)
Задача 1
В партии из 20 изделий 5 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 4 изделий 2 изделия являются дефектными?
Решение:
Воспользуемся классическим определением вероятности:
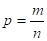
.
Где n — общее число исходов, m — число исходов, благоприятствующих событию. n — число вариантов взять наугад 4 изделия из 20 определяется по формуле:

Два дефектных изделия можно выбрать.
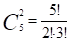
способами. Два годных изделия можно выбрать.
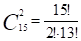
способами. По правилу произведения.
m =.
Находим искомую вероятность:
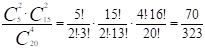
p = = 0,217.
Ответ: искомая вероятность равна 0,217.
Задача 2
В магазине выставлены для продажи 18 изделий, среди которых 6 изделий некачественные. Какова вероятность того, что взятые случайным образом 3 изделий будут некачественными?
Решение:
Посчитаем n — всевозможое число исходов — число способов выбрать 3 изделия из 18 имеющихся определяется по формуле:
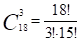
Посчитаем m — число исходов, благоприятных событию — количество способов выбрать 3 некачественых изделия из 6 имеющихся:

По классическому определению вероятности.
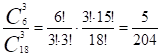
= = 0,025.
Ответ: искомая вероятность равна 0,025.
Задача 3
На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: 40 с первого завода, 35 со второго, 25 c третьего. Вероятность качественного изготовления изделий на первом заводе 0,9 на втором 0,7, на третьем 0,9. Какова вероятность того, что взятое случайным образом изделие будет качественным?
Решение:
Данная задача на применение формулы полной вероятности.
Пусть событие, А — взятое случайным образом изделие будет качественным.
Н1 — взятое случайным образом изделие изготовлено на 1-м заводе, Н2 — взятое случайным образом изделие изготовлено на 2-м заводе, Н3 — взятое случайным образом изделие изготовлено на 3-м заводе.
Н1, Н2 и Н3 — гипотезы; образуют полную группу событий.
Рассчитаем вероятности гипотез:
P (H1)= 40/(40+35+25) = 0,4.
P (H2)= 35/(40+35+25) = 0,35.
P (H3)= 25/(40+35+25) = 0,25.
По данным задачи условные вероятности равны:
PH1(A) = 0,9, PH2(A) = 0,7, PH3(A) = 0,9.
Найдем вероятность события, А по формуле полной вероятности:
Р (А) =.

P (A) = P (H1) · PH1(A) + P (H2) · PH2(A) + P (H3) · PH3(A) = 0,4 · 0,9 + 0,35 · 0,7 + 0,25 · 0,9 = 0,36 + 0,245 + 0,225 = 0,83.
Ответ: 0,83
Задача 4
Дано распределение дискретной случайной величины X.
Найти математическое ожидание и среднее квадратичное отклонение.
Xi. | — 6. | — 2. | ||
Pi. | 0,1. | 0,3. | 0,4. | 0,2. |
Решение:
Найдем М (Х) по формуле.
М (Х) =
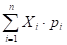
М (Х) = -60,1 + (-2)0,3 + 10,4 + 40,2 = -0,6 — 0,6 + 0,4 + 0,8 = 0.
Ско находим по формуле:
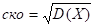
Найдем D (Х) по формуле.
D (Х) = M (X2) — [M (X)]2
M (X2) = 360,1 + 40,3 + 160,4 + 40,2 = 8,4.
D (Х) = M (X2) — [M (X)]2 = 8,4 — 02 = 8,4.
= 2,898.
Ответ: М (Х) = 0; ско = 2,898.
Задача 5
В городе имеются 3 оптовых базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0,1. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
Решение:
Обозначим через случайную величину Х — число баз, на которых искомый товар отсутствует в данный момент.
Случайная величина Х может принимать след. значения: 0; 1; 2; 3.
Наличие товара на той или иной базе — независимы один от другого события, вероятности отсутствия товара на каждой базе равны между собой, поэтому применима формула Бернулли.
Поскольку вероятность того, что товар на базе отсутствует, равна p=0.1, то вероятность того, что товар на базе есть q=1−0.1=0.9.
Найдем соответствующие вероятности:
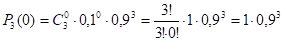
= 0,729.

= 0,243.

= 0,027.
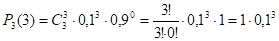
= 0,001.
Тогда закон распределения случайной величины Х в виде ряда распределения имеет вид:
X. | ||||
Pi. | 0,729. | 0,243. | 0,027. | 0,001. |
Ответ: закон распределения
Задача 6
Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно М (х) = 14, среднее квадратичное отклонение (ско) равно ско = 3. Найти вероятность того, что случайная величина в результате испытания примет значение в интервале (10, 15).
Решение:
Вероятность того, что нормально распределенная случайная величина Х примет значение, принадлежащее интервалу (б, в), равна:
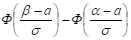
Р (б < X < в) = ,.
Где а — математическое ожидание, у — среднее квадратическое отклонение.
По условию задачи а = 14, у = 3, б = 10, в = 15. Следовательно, Р (10 < X < 15) = = =.

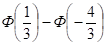
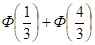
Находим значения по таблицам значений функции Лапласа.
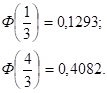
Тогда.

Р (10 < X < 15) = = 0,1293 + 0,4082 = 0,5375.
Ответ: Р (10 < X < 15) = 0,5375.
Задача 7
Рассчитать и построить гистограмму относительных частот по сгруппированным данным, где m — частота попадания в промежуток (xi, xi-1).
i. | xi < X < xi-1 | mi |
7−9. | ||
9−11. | ||
11−13. | ||
13−15. | ||
15−17. |
Решение:
Рассчитаем относительные частоты, как отношение частоты интервала к общему количеству вариантов.
Результаты занесем в таблицу:
i. | xi < X < xi-1 | mi | wi |
7−9. | 5/40= 0,125. | ||
9−11. | 4/40 = 0,1. | ||
11−13. | 8/40 = 0,2. | ||
13−15. | 12/40 = 0,3. | ||
15−17. | 11/40 = 0,275. | ||
Итого. |
Строим гистограмму.
Откладываем на горизонтальной оси (оси X) полученные интервалы. На них, как на основаниях, строим прямоугольники, высоты которых равны соответствующим относительным частотам интервалов. Полученная ступенчатая фигура и является искомой гистограммой.
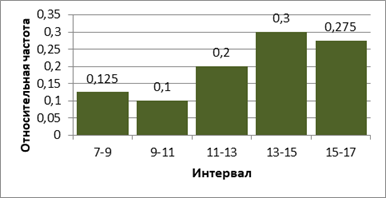
Рис. 1. Гистограмма интервалов
Задача 8
Найти несмещенную выборочную дисперсию на основании данного распределения выборки.
X. | 0,2. | 0,3. | 0,5. | 0,6. |
ni. |
Решение:
Несмещенную выборочную дисперсию находим по формуле:
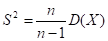
.
Где — выборочная дисперсия.
Найдем выборочную дисперсию по формуле:
D (Х) = M (X2) — [M (X)]2 ,.
М (Х) =

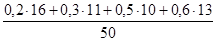
М (Х) = = 19,3/50 = 0,386.
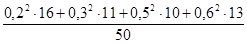
M (X2) = = 8,81 / 50 = 0,176.
Теперь можно найти выборочную дисперсию:
D (Х) = M (X2) — [M (X)]2 = 0,176 — 0,3862 = 0,027.
Находим несмещенную выборочную дисперсию:
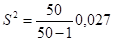
= 0,028.
Ответ: 0,028.
Задача 9
Решить задачу о замене оборудования, используя метод статистической игры без проведения эксперимента по критерию Байеса.
Оборудование после k лет может оказаться в одном из трех состояний: Q1 — оборудование вполне работоспособно и требует лишь небольшого текущего ремонта; Q2 — требуется серьезный капитальный ремонт; Q3 — дальнейшая эксплуатация оборудования невозможна. Вероятности этих состояний 0,2; 0,6; 0,2.
Q1. | Q2. | Q3. | |
А1. | |||
А2. | |||
А3. |
Для предприятия возможны три стратегии: A1 — остановить оборудование в работе еще на год, проводя незначительный ремонт; A2 — провести капитальный ремонт; A3 — заменить оборудование. Потери, которые несет предприятие при различных стратегиях, даны в таблице.
Решение:
По критерию Байеса, оптимальной будет та стратегия Аi при которой минимизируется величина среднего риска (средних потерь).
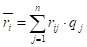
Рассчитаем средний риск для каждой стратегии:
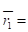
- 1?0,2 + 5?0,6 + 7?0,2 = 0,2 + 3 + 1,4 = 4,6
- 3?0,2 + 2?0,6 + 6?0,2 = 0,6 + 1,2 + 1,2 = 3
- 5?0,2 + 4?0,6 + 3?0,2 = 1 + 2,4 + 0,6 = 4


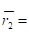
Среди найденных значений выбираем минимальное 3.
Следовательно, выбираем вторую стратегию А2.
Ответ: выбираем вторую стратегию А2 — провести капитальный ремонт.
Задача 10
Решить задачу выбора оптимального режима работы технологической линии по критерию Байеса.
На технологическую линию может поступать сырье с малым (Q1) и с большим (Q2) количеством примесей.
Априорные вероятности состоящий природы равны q1 = 0,4; q2 = 0,6. Для случаев использования различных видов сырья предусмотрены три режима работы технологической линии: А1, А2, А3. Потери, отражающие качество выпускаемой продукции и расходы сырья в зависимости от качества сырья и режима работы линии, приведены в таблице:
Q1. | Q2. | |
А1. | ||
А2. | ||
А3. |
вероятность математический квадратический выборка.
Решение:
По критерию Байеса, оптимальной будет та стратегия Аi при которой минимизируется величина среднего риска (средних потерь).
Рассчитаем средний риск для каждого режима технологической линии:
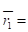
- 0?0,4 + 5?0,6 = 0 + 3 = 3
- 1?0,4 + 3?0,6 = 0,4 + 1,8 = 2,2
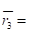
3?0,4 + 2?0,6 = 1,2 +1,2 = 2,4.
Среди найденных значений выбираем минимальное — 2,2.
Следовательно, выбираем второй режим работы технологической линии А2.
Ответ: выбираем второй режим работы технологической линии А2.
- 1. Баврин И. И. Теория вероятностей и математическая статистика. — М.: Высшая школа, 2005.
- 2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. — М.: Высшая школа, 2004.
- 3. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов.- М.: Высшая школа, 2009.
- 4. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов.— М.: ЮНИТИ, 2006.