Расчет сложных электрических цепей с постоянными и гармоническими напряжениями и токами по теоретическим основам электротехники

Расчет сложных электрических цепей с постоянными и гармоническими напряжениями и токами по теоретическим основам электротехники Задача № 1.

Для заданной схемы с постоянными во времени ЭДС и тока, принимая.

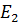
(t)=E; (t)=; j (t)=j.

Выполнить следующие:

Изобразить схему, достаточную для расчета токов во всех ветвях схемы и напряжение на источниках тока, используя два разных способа;

Рассчитать баланс вырабатываемой и потребляемой мощности;

Представить цепь относительно ветви ab активным двухполюсником, определить его параметры, построить внешнюю характеристику двухполюсника и по ней графически определить ток ветви 01 в;

Для любого контура без источника тока рассчитать и построить потенциальную диаграмму;

Определить показания вольтметра.

Задача № 2.

Для заданной схемы, с источником гармонических сигналов, принимая.

=314 рад/сек, М=L/2.

(t)= sin (t +).

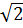
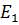
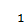
(t)= sin (t +).

J (t)= Jsin (t +).

Выполнить следующее:

Рассчитать комплексные сопротивления ветвей, соединяющих узлы, помеченные на схемах буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно п. 1 задачи 1, причем параллельное соединение R и C представить в виде одного комплексного сопротивления);

Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на источнике тока. Записать мгновенное значение тока ветви и ЭДС (t) и напряжение на источниках тока; напряжение ток электрический цепь Рассчитать баланс мощности активной и реактивной мощности;

Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжения;

Определить показания вольтметра;

Сделать развязку индуктивной связи и относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквивалентного генератора) Zr= * ЭДС генератора Er и ток Iab ветви ab, а затем при изменении сопротивления R ветви ab от 0 до 10*Zг рассчитать и построить зависимость активной мощности Pab=f®.

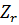
Проанализировать использованные методы расчета, результаты вычислений и сформировать выводы по работе.

Схема задания.

Введение

Цель данной работы состоит в ознакомлении с методами расчетов сложных электрических цепей с постоянными и гармоническими напряжениями и токами по теоретическим основам электротехники.

Линейные цепи постоянного тока Рассчитываем данную схему методом законов Кирхгофа:

Считаем, что нам известен один из токов (по условию I6=J=4 A), неизвестным будем считать напряжение на зажимах источника тока (Ucd).

Составим систему уравнений по законам Кирхгофа.

По первому закону:

Для узла а: I4 — I2 — I5 = 0.

Для узла b: I3 — I1 — I4 = 0.

Для узла с: J + I2 — I3 = 0.

По второму закону:

Для контура (dcbd): I3*2R — Ucd = E1.

Для контура (acba): I2*R + I3*2R + I4R = E2.

Для контура (dbad): I5*R + I4*R = -E1.

Cистема шести уравнений в матричной форме вида [A]*[X]=[B]:

X:=(А)-1 * В.

I1 = 4.347 A I2 = -1.306 A I3 = 2.694 A.

I4 = -1.653 A I5 = -0.347 A Ucd= 237.14 B.

Расчет методом контурных токов Считаем, что в цепи протекают три контурных тока I11, I22, I33. Один из контурных токов нам известен (I11=J=4 A), неизвестными будутI22, I33, Ucd.

Составим систему уравнений по методу контурных токов:

I контур (dcbd): I11*2R + I22*2R — Ucd = E1.

II контур (acba): I11*2R + I22*4R + I33*2R = E2.

III контур (dbad): I22*R + I33*2R = -E1.

В матричной форме виде [A]*[X]=[B] получим:

X:=(A)-1*B.

I22= -1.306 A I33= -0.347 A Ucd= 237.14 B.

напряжение ток электрический цепь По найденным контурным токам находим токи в ветвях:

I1 = I11 — I33 = 4.347 A I4 = I33 + I22 = -1.653 A.

I2 = I22 = -1.306 A I5 = I33 = -0.347 A.

I3 = I11 + I22 = 2.694 A I6 = J = 4 A.

Искомые величины в данном методе совпали с величинами, полученными методом законов Кирхгофа.

Баланс мощностей.

Вырабатываемая мощность:

PE1=E1*I1=140*4.347=608.57 Вт.

PE2=E2*I2=170*(-1.306)= -222.04 Вт.

PJ=Ucd*J=237.14*4=948.6 Вт.

P?ист=PE1 + PE2 + PJ= 608.57 + (-222.04) + 948.6= 1335.1 Вт Мощность потребляемая нагрузкой:

P1=I12*Rветви=0 Вт.

P2=I22*R=119.42 Вт.

P3=I32*2R=1016 Вт.

P4=I42*R=191.3 Вт.

P5=I52*R=8.426 Вт.

P?нагр= P1 + P2 + P3 + P4 + P5 = 1335.1 Вт.

P?ист = P? нагр

1335.1 = 1335.1 Вт.

Представим цепь относительно ветви ab активным двухполюсником и определим его параметры.

Для этого рассчитываем схему методом контурных токов. Считаем, что известно по условию I11=J= 4 A.

Контур (dcbd): I11X*2R — Ucdxx + I22X*2R = E1.

Контур (dacbd): I11X*2R + I22X*4R = E2 + E1.

— Ucdxx + I22X*2R = E1 — J*2R (1).

I22X*4R = E2 + E1 — J*2R (2).

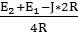
Из (2) I22X = = -0.893 A.

I2X = I22X = -0.893 A.

I3X = I11X + I22X = 3.107 A.

Из контура (dacbd) выразим Ubaxx:

I2X*R + I3X*2R + Ubaxx = E2.

Eген = Ubaxx = E2 — I2X*R — I3X*2R = - 202.5 B.

Находим Rген:

Схема активного двухполюсника:

Внешняя характеристика двухполюсника:

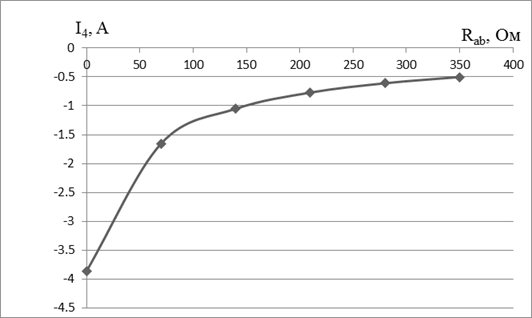
Потенциальная диаграмма.

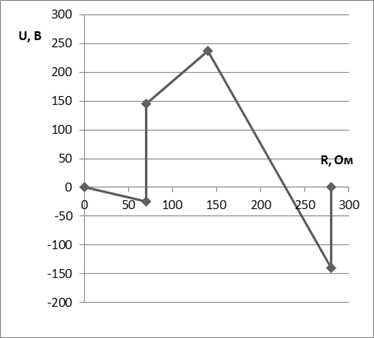
Показания вольтметра:

Uv = Ucb = I3*2R = 2,694*140 = 377,2 В Линейные цепи синусоидального тока.

e1(t) = *E1*sin (щt+ б1) = 140**sin (щt + 60o) B.

e2(t) = *E2*sin (щt+ б2) = 170**sin (щt — 30o) B.

J (t) = *J*sin (щt+ в) = 4**sin (щt+ 180o) A.

Взаимная индуктивность между катушками в ветвях ab и bc:

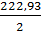
M = = = 111,465 мГн.

XМ = щ*M = 314*111,465*10−3= 35 Ом.

E1 = 140*e-j60 = 70 + j121,24 B.

E2 = 170*e-j30 = 147,22 — j85 B.

J = 4*ej180 = -4 + j0 A.

Рассчитываем комплексные сопротивления элементов ветвей соединяющих узлы:

XL= щ*L=314*222,93*10−3=70 Ом.

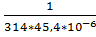
XC== = 70 Ом.

Z2 = R = 70 Ом.

Z3= 2R + jXL = 140 + j70 Ом.

Z4= R + jXL = 70 + j70 Ом.

Z5= = = 35 — j35 Ом.

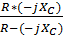
Не исключая индуктивных связей, определим комплексы действующих значений токов всех ветвей и напряжение на источнике тока.

По законам Кирхгофа составим систему уравнений:

По первому закону:

Для узла а: I4 — I2 — I5 = 0.

Для узла b: I3 — I1 — I4 = 0.

Для узла с: I + I2 — I3 = 0.

По второму закону:

Для контура (dcbd): I3*Z3 — I4jXМ — Ucd = E1.

Для контура (acba): I2*Z2 + I3*(Z3 — jXМ) + I4*(Z4 — jXМ) = E2.

Для контура (dbad): I5* Z5 + I4*Z4 — I3*jXМ = -E1.

Cистема шести уравнений в матричной форме вида [A]*[X]=[B]:

X:=(А)-1 * В.

Мгновенные значения:

i1 = 2.762**sin (щt + 99.7) A.

ucd = 309.921**sin (щt — 162.5) B.

Рассчитываем токи методом контурных токов с учетом магнитных связей.

Считаем, что в цепи протекают контурные токи I11, I22, I33(соответственно контурам схемы I, II, III).

Выразим токи в ветвях через контурные токи:

I1 = I11 — I33 I3 = I22 + I11 I5 = I33.

I2 = I22 I4 = I33 + I22 I6 = I11 = J = -4 + j0.

Подставим в (2):

(I22 + I11) Z2 — (I33 + I22) jXМ — Ucd = E1.

I22*Z2 + (I22 + I11) Z3 — (I33 + I22) jXМ + (I33 + I22) Z4 — (I22 + I11) jXМ = E2.

I33*Z5 + (I33 + I22) Z4 — (I22 + I11) jXМ = -E1.

I11*Z3 + I22(Z3 — jXМ) + I33(-jXМ) — Ucd = -E1.

I11(Z3 — jXМ) + I22(Z2 + Z3 — jXМ + Z4 — jXМ) + I33(-jXМ + Z4) = E2.

I11(-jXМ) + I22(Z4 — jXМ) + I33(Z5 + Z4) = -E1.

В матричной форме виде [A]*[X]=[B] получим:

X:=(A)-1*B.

I1= I11-I33= -0.467 + j2.722 A I4 = I33 + I22=-0.335 — j2.203 A.

I2 = I22= 3.199 + j0.519 A I5 = I33 = -3.534 — j2.722 A.

I3=I22+I11=-0.801+ j0.519 A Ucd = -295.66 — j92.95.

Искомые величины в данном методе совпали с величинами, полученными методом законов Кирхгофа.

Баланс мощностей.

Мощность нагрузки:

Љ2= I22*Z2 =(2.762)2*70 = 735.012 Вт.

Ucb= I3*Z3 — I4*jXМ = -225.66 + j28.29 B.

Љ3= Ucb*I3*=(-225.66 +j28.29)(-0.8014 — j0.519)= 195.54 + j94.46 Вт.

Uba= I4*Z4 — I3*jXМ = 148.96 — j149.63 B.

Љ4= Uba*I4*=(148.96 — j149.63)(-0.335 + j2.203)= 279.8 + j378.3 Вт.

Љ5= I52*Z5= (4.461)2*(35 — j35) = 696.4 — j696.4 Вт.

Љ?нагр= Љ2+ Љ3+ Љ4+ Љ5= 1907 — j223.62 Вт Мощность источников питания:

Љe1= E1*I1* =(70 + j121.24)(-0.467 — j2.722)= 297.41 — j247.13 Вт.

Љe2= E2*I2*=(147.22 — j85)(3.199 — j0.519)= 426.71 — j348.3 Вт.

ЉJ=Ucd*J*=(295.65 — j92.95)(-4 -j0)= 1183+j371.8 Вт.

Љ?ист= Љe1+ Љe2+ ЉJ= 1907 — j223.62 Вт.

Љ?нагр = Љ?ист Сделаем развязки индуктивных связей в схеме, выделим из схемы ветвь ab и определим параметры активного двухполюсника.

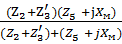
Zген=Zabxx= = 30.1 + j0.7 Ом.

Oпределим параметры активного двухполюсника.

I11X (Z3' + jXM) + I22X (Z3' + jXM) = E1 + Ucdxx.

I11X (Z3' + jXM) + I22X (Z3' + jXM + Z5 + Z2)= E1 + E2 (2).

Из (2) I22X= = 3.29 + j0.821 A.

I2X= I22X= 3.29 + j0.821 A.

I3X= I11X + I22X= -0.71 + j0.821 A.

Ubaxx + I2X*Z2 + I3X*Z3'=E2.

Eген=Ubaxx=E2 — I2X*Z2 — I3X*Z3'= 45.133 — j232.51 B.

Изменяя сопротивление ветви ab от 0 до 10*Zген, рассчитываем и построим зависимость Pab = f (Rab).

Лучевая диаграмма и совмещенная с ней топографическая диаграмма напряжений.

Показания вольтметра:

Uv = [Ucb]= [цc — цb] = [-225,66 + j28,3] = [227,4ej172,9] = 227,4 В Заключение Данный курсовой проект предусматривает практическое применение изученных правил расчёта электрических цепей. Для расчёта тока применяется закон Ома и правило Кирхгофа. Различные методы расчёта предусматривают широкий диапазон использования схем соединения резисторов, катушек и конденсаторов, как для цепей постоянного тока, так и для цепей переменного тока. Правильность всех расчётов проверяется составлением баланса мощностей, что подтверждает положение о сохранении энергии. Построение векторных и типографических диаграмм для цепей переменного тока даёт чёткое представление о синусоидально изменяющихся напряжениях и токах, характеризующихся не только амплитудной (действующими значениями), но и начальной фазой.

Список литературы

Бессонов Э. А. «Теоретические основы электротехники» 2012.

Зевеке Г. В. «Основы теории цепей» 2010.

Стабеков Г. И. «Теоретические основы электротехники. Часть I» 2009.