Методы определения порядка реакции

I. Если дифференциальное кинетическое уравнение реакции имеет вид:

то порядок реакции (n) можно определить по результатам кинетического опыта:

одно из следующих способов:

• 1. метод подстановки (применяют, если есть основания полагать, что порядок реакции целый: n=1,2, или 3). По опытным значениям концентраций в различные моменты времени рассчитывают величину константы скорости по уравнению первого (1.14), второго (1.21) и третьего порядка. Можно считать, что процесс описывает то уравнение, для которого рассчитанные значения константы колеблются около некоторой средней величины с отклонениями в пределах возможной ошибки эксперимента.
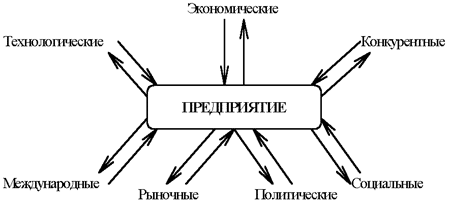
• 2. графический метод. Зависимость концентрации реагентов от времени для реакций различных порядков может быть изображена прямой линией, если выбрать соответствующую систему координат. Так для реакций 1-ого порядка прямая получается в координатах lnc — t (рис. 1.4), для 2-ого порядка при в координатах (рис. 1.6) и для 3-его порядка в системе координат 1/с² — t. Если прямая получается в какой-то из указанных систем координат, становится ясным порядком реакции, а по наклону прямой к оси абсцисс можно определить и ее константу.
• 3. по периоду полураспада. Чтобы определить порядок реакции этих методом следует выяснить, как зависит время полупревращения исходного вещества, А от его начальной концентрации c_0. Как уже было показано (см. уравнение (1.25)), время полупревращения (ф) обратно пропорционально начальной концентрации исходного вещества (c₀) в степени на единицу меньшей, чем порядок реакции. Если построить график в координатах отlgc₀, то порядок реакции можно определить по углу наклона прямой к оси абсцисс: tgб = n-1. Чтобы получить необходимые для построения прямойданные:

Начальная концентрация исходного вещества с0		…
Период полураспада ф.	ф1	ф2	ф3	…

Нужно провести несколько опытов с различной начальной концентрацией реагента (с₀) или проанализировать результаты одного опыта, принимая каждый из последующих моментов времени за нулевой, а концентрацию в этот момент за начальную концентрацию (см. рис. 1.8).

4. метод начальных концентраций. По этому методу нужно исследовать зависимость начальной скорости реакции (т.е. скорости при t= 0) от исходной концентрации реагента (с0).

Поскольку.

lg х₀ = lgk + nlgc₀ (1.28).

И в координатах lgх₀— lgc₀должна получиться прямая линия, тангенс угла наклона которой к оси абсцисс будет равен порядку реакцииn (tgб = n). Начальную скорость х₀можно определить по кинетической кривой, или используя выражение для средней скорости реакции за небольшой начальный период времени:

где ?tнебольшой интервал времени после начала реакции;

?сизменение концентрации за время? t.

Реакцию, как и в предыдущем случае, необязательно начинать каждый раз сначала. Можно принять любой момент времени за нулевой и определить в этот момент скорость реакции.

II. Если начальные концентрации реагентов неодинаковы, то для протекающей при постоянном объеме реакции:

х ₁А+х ₂В+ х ₃С>Продукты дифференциальное кинетическое уравнение имеет вид:

где n=n₁+n₂+n₃— порядок реакции.

Для определения порядка реакции в целом (n) необходимо сначала установить порядок реакции по каждому из реагирующих веществ (n₁, n₂, n₃). Сумма порядков по каждому веществу и дает порядок реакции в целом. В таких случаях обычно применяют Метод понижения порядка реакции.

Чтобы определить порядок реакции по веществу A, нужно при проведении кинетического опыта создать такие условия, при которых в процессе реакции менялась бы только концентрация вещества A, а концентрации остальных реагентов оставались бы практически постоянными, для этого все реагирующие вещества, кроме A, берут в таком большом избытке, чтобы изменением их концентрации во времени можно было бы пренебречь. Поскольку концентрации веществ B и C остаются постоянными (C_В=const, C_С=const), дифференциальное уравнение (1.30) можно переписать в виде.

и определить n₁ одним из четырех описанных выше методов.

Затем проводят кинетический опыт так, чтобы, А и С были в большом избытке по сравнению с В и определяютn₂ в уравнении:

И, наконец, для определения порядка реакции по веществу С (n₃) проводят опыт при большом избытке, А и В.

Задача № 1.

Реакция при температуре 50? С протекает за 2 мин 15с. За сколько времени закончится эта реакция если при температуре 70? С, если в данном температурном интервале температурный коэффициент скорости реакции равен 3?

Решение.

При увеличении температуры с 50? С до 70? С скорость реакции в соответствии с правилом Вант-Гоффа возрастает.

где, а и — скорость реакции при данных температурах. Получаем.

т.е. скорость реакции увеличится в 9 раз.

В соответствии с определением скорость реакции обратно пропорциональна времени реакции, следовательно,.

где — время реакции при температурах .

Отсюда получаем.

Учитывая, что =135с (2мин 15с), определяем время реакции при температуре :

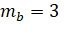
Задача № 2.

Провести численный расчет кинетики реакции Лотки-Вольтера.

.

получить в символьном виде выражения для стационарных решений и собственных значений для системы дифференциальных уравнений, описывающей концентрации X и Y.

Решение.

Решим данную задачу с помощью математического пакета Mathcad.

Запишем исходные данные и систему дифференциальных уравнений.

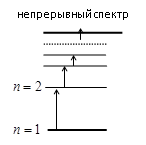
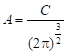
Для выяснения особенностей кинетики данной реакции достаточно рассмотреть подсистему из (2) и (3) уравнений, поскольку продукты D и E далее ни в каких реакциях не участвуют.