Оценка качества последовательности случайных чисел

Оценка качества последовательности случайных чисел проводится методами математической статистики. Это стандартная задача проверки статистической гипотезы о типе распределения вероятности.

Допустим, что генератор создает последовательность случайных чисел с равномерным на интервале [0, 1) законом распределения вероятности (статистическая гипотеза). Определим вероятность этого предположения.

Для проверки гипотезы необходимо выполнить следующие действия:

• 1. разбить интервал [0, 1) на m частей (m = 20 — 50);
• 2. определить число v_j случайных чисел u_i, попадающих в каждый интервал;
• 3. определить теоретическое число w_j равномерно распределенных случайных чисел, которые должны попасть в эти интервалы;
• 4. вычислить значение критерия Пирсона ч²;
• 5. по таблице распределения ч² найти вероятность правильности статистической гипотезы.

Проведем проверку статистической гипотезы о равномерности распределения последовательности случайных чисел, полученной в п. 1.2.

Разобьем интервал 0? x < 1 на m = 5 частей (в последовательности всего N = 25 чисел).

Построим гистограмму попаданий случайных чисел экспериментальной и теоретической последовательности в эти интервалы.

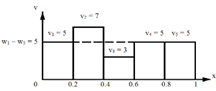
v₁ — v₅ — экспериментальная,.

w₁ — w₅ — теоретическая.

Рисунок 1. Гистограммы попаданий случайных чисел в интервалы.

Рассмотрим функцию равномерного распределения плотности вероятности на интервале [0, 1).

Рисунок 2. Функция плотности вероятности для последовательности равномерно распределенных случайных чисел.

Функция распределения вероятностей связана с функцией плотности распределения вероятностей следующим соотношением.

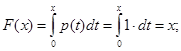
(1).

График функции равномерного распределения вероятности представлен на следующем рисунке.

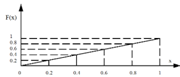
Рисунок 3. Функция распределения вероятности для последовательности равномерно распределенных случайных чисел.

Вероятность попадания случайной величины в каждый интервал на оси x равна

(2).

Тогда число случайных чисел последовательности длиной N, которые теоретически должны попасть в каждый интервал, равно.

(3).

Гистограмма теоретического распределения числа попаданий равномерно распределенных случайных чисел в интервалы показана на рисунке 1 пунктиром.

Понятно, что чем ближе теоретическая и экспериментальная гистограммы, тем ближе распределение вероятности случайных чисел экспериментальной и теоретической последовательности. Это простое соображение положено в основу критерия согласия Пирсона (критерия ч²).

Количественную оценку близости теоретического и экспериментального распределения вероятности случайных величин по критерию Пирсона находят следующим образом. Вычисляем значение ч² по следующей формуле.

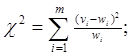
(4).

Для нашего примера значение ч² = 1.6; Дальше необходимо взять таблицу распределения ч² и по ней определить вероятность выдвинутой статистической гипотезы. В эту таблицу, кроме значения ч² входит второй параметр — число степеней свободы n. Число степеней свободы n на единицу меньше числа интервалов m на гистограмме.

(5).

Для рассматриваемого примера число степеней свободы n = 4.

В результате по таблице находим, что вероятность выдвинутой статистической гипотезы равна 0.81 (81%). Как относиться к этому результату? Понятно, что если вероятность правильности статистической гипотезы мала (обычно меньше 70%), то результат нельзя считать хорошим. Аналогично обстоит дело и с очень высокой вероятностью правильности статистической гипотезы (обычно больше 95%). В этом случае, возможно, что последовательность чисел не является случайной.

Проверку статистической гипотезы по критерию ч² удобно проводить средствами программы Microsoft Excel. Для этого необходимо загрузить числа из экспериментальной и теоретической гистограмм в ячейки программы Excel и вызвать функцию ХИ2ТЕСТ. Для примера на рисунке 1 получим:

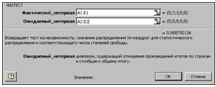
Рассмотренная схема проверки статистических гипотез работает и для случайных величин с произвольным распределением вероятности. Аналогичным образом строится экспериментальная и теоретическая гистограммы и вычисляется значение ч² по формуле (4). При построении теоретической гистограммы число случайных величин w_i, которые должны попасть в каждый интервал, вычисляется по формуле (3). Вероятность попадания числа в каждый интервал ДP_i определяется по формуле (2), при этом в общем случае эти вероятности разные.

При выполнении лабораторной работы число случайных чисел в последовательности N имеет порядок 15 — 20 тыс. Число интервалов m на гистограмме необходимо выбирать порядка 20 — 50. Удобнее всего выбирать m из ряда чисел 21, 31, 41 и т. д., что позволяет получить удобные значения для числа степеней свободы n = 20, 30, 40 и т. д. Эти числа обычно указываются в таблице распределения ч² .