Автоматные модели адаптивных систем управления

(СУ). Рассмотрим возможность применения ВА для задач моделирования адаптивных СУ, в частности систем, в которых реализован принцип обучаемости в поведении, исходя из анализа сигналов обратной связи. Особенность данного моделирования состоит в том, что оно осуществляется в условии отсутствия априорных сведений о модели объекта [11].

Моделирование целесообразного поведения автоматов в случайных средах. Структура взаимодействия автоматной системы с внешней средой приведена на рис. 5.2.

Выходные сигналы yt автоматной СУ, которую в дальнейшем будем называть автоматом, подаются на вход внешней среды. В терминологии теории игр эти сигналы называются действиями. Входные сигналы хt для автомата называются реакциями среды. Весь класс реакций подразделяется на два подкласса: класс положительных реакций и класс отрицательных реакций.

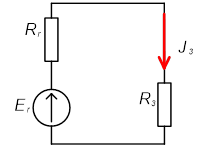
Рис. 5.2.

Модель случайной среды представим в виде вектора С=(a1,a2,…, ar), физический смысл элементов которого раскроем немного позже. Если автомат совершил действие yj (t) (j=1,2,…, r) в такте времени t, то с вероятностью qj он получит сигнал поощрения х1 либо с вероятностью рj сигнал наказания х2 в такте времени (t+1), причем вероятности определяются следующим образом:

Вероятности отвечают условию нормирования, а исходя из определения qj-рj=aj, мы видим, что аj есть математическое ожидание выигрыша автомата за действие yj.

Функционирование системы «автомат-среда» описывается марковской моделью. Доказать это можно следующим образом.

Смена состояний автомата определяется матрицами переходных вероятностей, которые зависят от входного сигнала. Пусть в такте t автомат находился в состоянии zt, а на выходе был сигнал yt. Вероятность перехода автомата из состояния zр в состояние zk определится.

ррk=qjрk (х1)+рjрk (х2),.

где рk — вероятность перехода из состояния zр в состояние zk при соответствующем входном сигнале х. Причем.

Строки стохастической матрицы ||ррk|| являются нормированными, следовательно, поведение системы «автомат-среда» описывается марковским процессом.

Если конструкция автоматов такова, что цепь Маркова будет эргодической, то существуют финальные вероятности состояний, не зависящие от начальных состояний.

Пусть финальные вероятности состояний — rj, а финальные вероятности действий — j. Финальная вероятность действия yj будет определяться суммой финальных вероятностей тех состояний, в которых автомат осуществляет действие yj.

Математическое ожидание выигрыша автомата в среде СМ (А, С) за один шаг будет определяться по формуле [12].

причем.

Если автомат выбирает любое из действий равновероятно, то математическое ожидание выигрыша определится по формуле.

Говорят, что автомат обладает целесообразным поведением, если математическое ожидание выигрышей за один шаг отвечает условию.

М (А, С)>М0.

Задача построения автомата, обладающего целесообразным поведением, на первый взгляд тривиальна.

Действительно, это автомат с одним состоянием и он выполняет одно действие, за которое получает максимальный выигрыш. Но это автомат с «априорной целесообразностью», который заранее знает действие, за которое получает наибольший выигрыш. Такие автоматы исследовать не имеет смысла.

Будем рассматривать автоматы, не обладающие «априорной целесообразностью» .

Модель среды задается в виде вектора С=(a1,a2,…, ar). Следовательно, автомат будет обладать целесообразным поведением тогда, когда его поведение целесообразно в r! средах, получаемых из среды С. Это говорит о том, что функция М (А, С) является симметрической функцией параметров аi. Автомат, обеспечивающий такую функцию, называется симметрическим автоматом.

Известны две модификации симметрических автоматов [12]. При выигрыше автомат сохраняет свое состояние, а при проигрыше автомат изменяет свое состояние с вероятностью либо сохраняет свое состояние с вероятностью 1-. Рассмотрим графы, которые отображают переходы автомата.

Для первой модификации автомата смена состояний при проигрыше осуществляется циклически, как это показано на рис. 5.3, а для второй модификации автомата при сигнале проигрыша возможен равновероятный переход в любое другое состояние.

Граф переходов автомата второй модификации приведен на рис. 5.4.

Матрица вероятностей функции переходов автомата первой модификации автомата (см. рис. 5.3) при получении сигнала наказания имеет вид.

Рис. 5.4.

Матрица вероятностей функции переходов автомата второй модификации автомата (см. рис. 5.4.) при получении сигнала наказания имеет вид:

Доказано [12], что симметрический автомат при любых 0 обладает в стационарной среде целесообразным поведением.

Математическое ожидание выигрышей симметрического автомата можно увеличить, если применить автомат, представляющий собой композицию двух автоматов: автомата памяти B и симметрического автомата Tr, как это показано на рис. 5.5.

Рис. 5.5.

Семейство асимптотически оптимальных автоматов. Рассмотрим построение автоматов, обладающих асимптотической оптимальностью.

Автомат с линейной тактикой символически обозначается как Lmr-автомат. В этом обозначении m — емкость памяти автомата, r — число действий. Структура данного автомата приведена на рис. 5.6.

Рис. 5.6.

Автомат памяти B, как это видно из рис. 5.6, состоит из r изоморфных подавтоматов, определенных «ветвями» состояний. Симметрический автомат Tr реализован на состояниях. Если автомат находится в состояниях, то он выдает действие yj.

При сигнале х1 (поощрение) автомат меняет состояние в сторону увеличения нижнего индекса, а если он находился в крайнем наибольшем по нижнему индексу состоянии zm, то сохраняет свое состояние.

При сигнале х2 (наказание) автомат, если он находился не в крайнем наименьшем по нижнему индексу состоянии, меняет свое состояние в сторону уменьшения нижнего индекса. Если же автомат находился в состоянии, то автомат переходит в состояние, а при ir — в состояние .

На рис. 5.7 приведен граф переходов автомата В. И. Кринского (доверчивый автомат), условно обозначаемого Dmr. При получении сигнала х1 (поощрение) он переходит в глубокое состояние. В остальном алгоритм работы соответствует автомату с линейной тактикой.

Известны асимптотически-оптимальные последовательности автоматов, в которых смена состояний осуществляется по рандомизированным правилам.

На рис. 5.8 приведен граф переходов автомата В. Ю. Крылова, обозначаемого символом Kmr. При выигрыше автомат Kmr ведет себя так, как и автомат Lmr, а при проигрыше автомат с вероятностью р+=0.5 увеличивает индекс состояния в большую сторону либо с вероятностью р-=0,5 уменьшает индекс состояния (ir). При j=1 автомат с вероятностью рможет изменить действие на yi+1, если ir, и на y1, если i=r.

На рис. 5.9 приведен граф смены состояний для автомата, известного под названием «квазилинейный автомат». Этот автомат имеет символическое обозначение Qmr.

При сигнале х1 смена состояний осуществляется в соответствии с вероятностями q+ (в сторону увеличения индекса) и q-(в сторону уменьшения индекса). При сигнале х2 смена состояний осуществляется с вероятностями р+ и ртак же, как и у автомата Kmr.

Рис. 5.8.

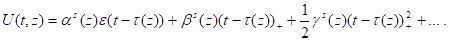
Формально смена состояний осуществляется следующим образом. Если в такте t-1 автомат был в состоянии и поступил в такте t сигнал х1, то при j= автомат с вероятностью qперейдет в состояние zij-1 и с вероятностью q+ перейдет в состояние .

Из состояния автомат с вероятностью qперейдет в состояние и с вероятностью q+ останется в состоянии. Из состояния с вероятностью q+ перейдет в состояние и с вероятностью qсменит действие, т. е. при ir перейдет в состояние, а при i=r перейдет в состояние .

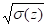
Рис. 5.9.

Если в такте t-1 автомат был в состоянии и в такте t поступил сигнал «наказание», то при j= автомат с вероятностью рпереходит в состояние и с вероятностью р+ переходит в состояние. Из состояния автомат с вероятностью рпереходит в состояние и с вероятностью р+ останется в состоянии. Из состояния автомат с вероятностью р+ переходит в состояние и с вероятностью рсменит действие. Если ir, то автомат переходит в состояние, а при i=r в состояние .