Лекция 2. Энтропия

Как уже говорилось выше, если источник выдает цифры 0 и 1 с одинаковой вероятностью ½, то количество информации, приходящейся на одну цифру равноlog₂(½)=1 биту. Предположим теперь, что цифры появляются с различной вероятностью, P (0)=p, P (1)=q=1-p. Тогда количество информации, содержащейся в одной цифре так же будет различным. Если P (0)=0.99 и P (1)=0.01, то количество информации, соответствующей цифре «0» будет равноlog₂(0.99)=0.0145 битов, а цифре «1» — -log₂(0.01)=6.64 бита.

Пусть мы имеем достаточно длинное (длины n) сообщение в таком алфавите. В нем «0» появится в среднем p*n раз, а «1» — q*n=(1-p)*n раз. Учитывая количество информации, содержащейся в каждой цифре, мы можем сказать, что общее количество информации в сообщении длины n равно.

— p*n*log (p) — q*n*log (q) = n*(- p*log (p) — q*log (q)),.

а среднее количество информации, приходящееся на один символ, равно.

— p*log (p) — q*log (q).

Переходя к общему случаю, мы получим следующий результат.

Пусть алфавит состоит из N различных символов, которые появляются с вероятностями p (1),…, p (N) независимо друг от друга. Тогда среднее количество информации, приходящееся на один символ, равно.

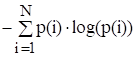
H = - p (1)*log (p (1)) — … — p (n)*log (p (N)) = .

Такая величина определяет среднее количество бит, приходящихся на один символ информационного потока, и называется энтропией заданного потока символов.

Для двухсимвольного алфавита, если вероятности появления символов одинаковы и равны ½, то энтропия потока равна 1 бит/символ. Если же P (0)=0.99, P (1)=0.01, то энтропия потока примерно равна 0.08 бит/символ. Подчеркнем, что эти рассуждения применимы только в потоку независимых символов, когда вероятность появления очередного символа не зависит от предыдущих.

Если в алфавите m символов и вероятности их появления равны (и составляют 1/m), то энтропия для одного символа данного алфавита будет равна.

.

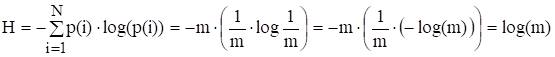
Считается, что нельзя закодировать текст таким образом, при котором среднее число битов на символ (средняя энтропия) будет меньше данного значения. Например, если сообщение состоит из букв русского алфавита, и вероятности появления всех букв одинаковы, то энтропия (среднее количество бит на один символ сообщения) будет равна.

H = log₂(33) = 5,44 394 бита.

При проектировании вычислительной техники в силу ее универсальности вероятности появления различных символов обычно считают одинаковыми. При этом энтропия показывает, какое минимальное количество бит требуется для кодирования одного символа заданного алфавита. Для 33 символов русского языка требуется, как показано выше, 5,044 бита. Однако для физической (аппаратной) реализации может быть выбрано только целое количество бит. Таким образом, округляя величину 5,044 к ближайшему большему целому, получаем, что для кодирования 33 символов требуется 6 бит. Если бы число букв в русском языке было равно 32, то энтропия была бы равной 5, и для кодирования букв требовалось бы ровно 5 двоичных разрядов.

Свойства энтропии:

• 1. Энтропия Н — величина вещественная, неотрицательная и ограниченная, т. е. Н 0. Это свойство следует из того, что такими же качествами обладают все ее слагаемые P (i) *log P (i).
• 2. Энтропия равна нулю, если сообщение известно заранее (в этом случае каждый элемент сообщения замещается некоторым знаком с вероятностью, равной единице, а вероятности остальных знаков равны нулю).
• 3. Энтропия максимальна, если все знаки алфавита равновероятны, т. е. Н_max = log m.

Для решения различных задач, связанных с кодированием текстовой информации, используется таблица частот появления букв русского алфавита. Аналогичные таблицы существуют для всех языков.