Решение задач. 
Задачи линейного программирования

Решение задачи линейного программирования

Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции.

Составим целевую функцию и зададим ограничения.

Пусть Х1, Х2, Х3, Х4, Х5 — неизвестные переменные Целевая функция: L (Х) = 14 х-9×2 — х4+6,4×5-> min;

Ограничения: g1: 0,9 х + 10×2−28×4 +5×5 245,.

g2: 0,8 х+ 1,7×2 -0,2×3 -0,5×4 =9,.

g3: 6 х + 4×3 — 7×4 + 6,3×5 54,.

g4: 8 х+6,2×2 -4,8×4 +2,9×5 17,.

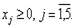
Ввод данных.

• 1. Введем на рабочий лист Excel необходимые данные. В ячейке В5 запишем выражение целевой функции, а в ячейках В8: В11 — левые части ограничений.
• 2. Командой Сервис, Поиск решения откройем диалоговое окно ІПоиск решенияІ (рис. 2) и заполним его данными. В поле Установить целевую ячейку введем адрес целевой функции $В$ 5, в поле Изменяя ячейки — адреса $B$ 3:$E$ 3. Переведите переключатель Равной в положение минимальному значению.

Чтобы ввести ограничения в окне ІПоиск решенияІ нажмем кнопку Добавить и на экране появится диалоговое окно ІДобавление ограниченияІ.

3. Начнем с первого ограничения. Установим курсор в поле Ссылка на ячейку и, выделяя на листе (рис. 1) ячейку В8, введем ее адрес $B$ 8 в это поле.

Кнопкой-стрелкой откроем список и выберем в нем знак <=. В поле Ограничение установите курсор и, выделяя на листе ячейку D8, введем ее адрес $ D $ 8 в это поле и нажмем кнопку Добавить.

4. Повторим действия п. 3 и введем остальные ограничения $В$ 9=$D$ 9, $В$ 10=$D$ 11, реализующие граничные условия. После ввода последнего ограничения $F$ 11<=$H$ 11 вместо кнопки Добавить нажмем кнопку ОК.

Таким образом, в окно ІПоиск решенияІ (рис. 2) будут введены ограничения.

Решение задачи.

1. Для задания необходимых параметров оптимизации нажатием кнопки Параметры откроем окно ІПараметры поиска решенияІ.

В этом окне оставьте неизменными установленные по умолчанию Максимальное время: 100 сек, выделяемое на поиск решения (возможно до 9 часов), Предельное число итераций: 100, Относительная погрешность: 0,1, Допустимое отклонение: 5%, переключатели в положении линейная, прямые, Ньютона.

Установим флажок Линейная, чтобы обеспечить применение симплекс-метода, и нажмите кнопку ОК.

2. В окне ІПоиск решенияІ нажмите кнопку Выполнить. На экране появится диалоговое окно ІРезультаты поиска решенияІ (рис. 5) с информацией «Решение найдено. Все ограничения и условия оптимизации выполнены», подтверждающей успешное решение задачи оптимального распределения ресурсов и количественные результаты (значения переменных, ограничений и целевой функции), приведенные на рис. 6.

x1 = А3 = 0, x2 = В3 = 14,43, x3 =С3 = 39,93, x4 =D3 =15,10, x5 =Е3=0 L= В5 = -144,99.

Анализ оптимального решения Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно ІРезультаты поиска решенияІ. С его помощью можно подготовить три типа отчетов: по результатам (опция Результаты), по устойчивости (опция Устойчивость), по пределам (опция Пределы).

1. Подготовим отчет по результатам (рис. 7).

Отчет состоит из трех таблиц.

В первой таблице (Целевая ячейка) приводятся сведения о целевой функции: исходное значение (в графе «Исходно») и оптимальный результат (в графе «Результат»).

Во второй таблице (Изменяемые ячейки) приводятся исходные (в графе «Исходно») и полученные в результате решения задачи (в графе «Результат») значения переменных x1, x2, x3, x4, x5.

Третья таблица (Ограничения) отображает результаты оптимального решения, касающиеся ограничений и граничных условий.

2. Щелчком на ярлычке Отчет по устойчивости откроем содержимое отчета на рабочем листе (рис. 8).

Отчет по устойчивости содержит две таблицы.

В первой таблице (Изменяемые ячейки) приводятся следующие значения переменных:

• · результаты решения задачи (графа «Результ. значение»);
• · нормированная стоимость, т. е. дополнительные двойственные переменные vj,, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

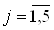
• · коэффициенты целевой функции (графа «Целевой коэффициент»);
• · предельные значения приращения коэффициентов Dcj целевой функции (последние две графы), при которых сохраняется набор переменных, входящих в оптимальное решение.

Во второй таблице приводятся значения ограничений:

• · значения используемых (графа «Результ. Значение») и заданных (графа «Ограничение, правая часть») ресурсов;
• · теневая цена, т. е. двойственные оценки zi, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
• · значения приращения ресурсов Дbi (последние две графы), при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
• 3. Отчёт по переделам (рис. 9) показывает, в каких пределах может меняться выпуск продукции, вошедшей в оптимальное решение, при сохранении его структуры:
  • · приводятся значения хi в оптимальном решении (графа «Значение»);
  • · даются нижние и верхние пределы изменения хi и соответствующие значения целевой функции (в графах «Целевой результат»).

линейный программирование транспортный симплекс.