Гидрогеологические расчеты водоносного горизонта

Задача 1

Определить единичного расхода для плоского потока грунтового водоносного горизонта.

Решение.

1. Определяем единичный расход для плоского потока грунтового водоносного горизонт q.

Так как водоносный пласт однороден по водопроницаемости и водоупорное ложе горизонтально, то для вычисления q можно применить уравнение.

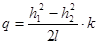
(1),.

где: k — коэффициент фильтрации пласта, м/сут;

h₁ — мощность водоносного горизонта в скважине, м;

h₂ — мощность водоносного горизонта в речной долине, м;

l — расстояние между скважинами, м;

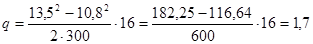
• 1,7 м³/сут — расход потока на 1 м.
• 2. Расход потока при заданной ширине 1,5 км будет равен

(2).

Где q — единичный расход потока, м³/сут;

Q — общий расход потока, м³/сут;

B — ширина потока, м.

Расход потока равен:

3. Определение ординат кривой депрессии выполняем по формуле:

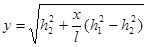
(3).

Где y — мощность потока воды на расстоянии x от речной долины, м Задаваясь различными значениями х получаем последовательно значения y₁, y₂ и т. д.

При х₁ = 50 м.

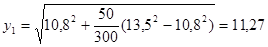
м;

Аналогично вычисляем значения у сотвествующие другим значениям х, данные расчета приведены в таблице 1.

грунтовый водоносный скважина суперпозиция Таблица 1.

По полученным данным строим кривую депрессии.

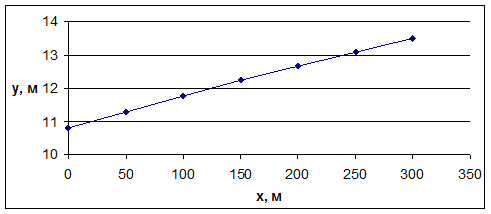
Рис. 2 Кривая депрессии через каждые 50 м

Ответ

Единичный расход потока грунтовых вод равен 1,7 м³/сут Расход при ширине 150 км равен 262,44 м³/сут Мощность потока воды увеличивается при расстоянии через каждые 50 м, по ним построена кривая депрессии.

Задача 2

Решение Определяя подпор в скважине № 1 имеем горизонтальный однородный пласт. Предположим, что расход потока при подпоре не измениться, тогда величину подпора можно определить по уравнению:

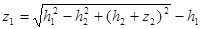
(4).

Где z₁ — подпор в скважине 1.

z₂ — известный подпор в реке.

h₁ — мощность потока в скважине 1.

h₂ — мощность потока уреза реки Величина подпора в скважине 1:

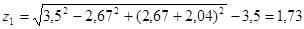
м Абсолютная отметка уровня грунтовых вод :

м Для расчета подпора в скважине 3, в которой наклонное строение пласта, используем формулу:

(5).

где h3 и h1 — мощность потока грунтовых вод соответственно в верхнем и нижнем сечениях;

H₃ и H₁ — абсолютные отметки уровня грунтовых вод в тех же сечениях;

z ₁ — известный подпор грунтовых вод в нижнем сечении;

z ₃ — неизвестный подпор грунтовых вод в верхнем, расчётном сечении.

Подпор в скважине 3:

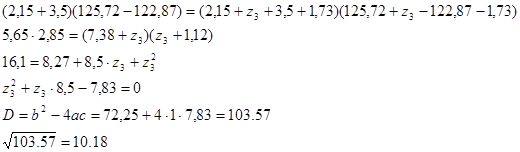
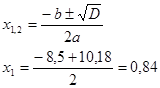
Величина подпора в скважине 3:

z₃ = 0,84 м Абсолютная отметка уровня грунтовых вод :

H₃ = 126.56 м.

Расчет подпора в скважине 2. Выполняем по той же формуле в которой наклонное строение пласта, используем формулу:

(6).

где h₂ и h₃ — мощность потока грунтовых вод соответственно в верхнем и нижнем сечениях;

H₂ и H₃ — абсолютные отметки уровня грунтовых вод в тех же сечениях;

z ₃ — известный подпор грунтовых вод в нижнем сечении;

z ₂ — неизвестный подпор грунтовых вод в верхнем, расчётном сечении.

Подпор в скважине 2:

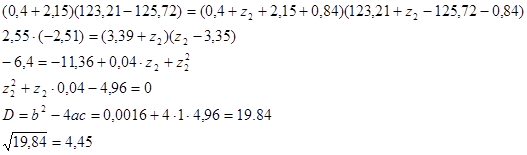
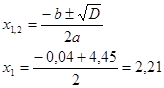
Величина подпора в скважине 3:

z₂ = 2,21 м Абсолютная отметка уровня грунтовых вод :

Н₂ = 125,42 м Ответ:

Подпор грунтовых вод в скважинах 1, 2 и 3 соответственно равны 124,6 м, 125,42 м и 126,56 м.

Задача 3

Решим задачу для водоносного горизонта с граничными условиями І-го рода. Для этого необходимо составить и решить следующую систему уравнений:

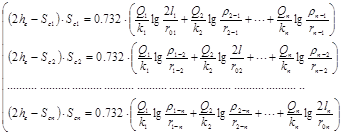
(7).

где: hе — естественная мощность водоносного горизонта, м;

Sп — понижение уровня воды в скважине, м;

r — расстояние между скважинами, м;

с — расстояние от расчетной скважины до зеркально отображенной, м;

Qп — дебит п-ной скважины, м³/сут.

Для расчета используем метод суперпозиции и зеркальных отражений. Расстояния от расчетной скважины до фиктивной выполняем с учетом параметра несовершенства гидравлической связи реки и водоносного горизонта (ДL), т.к. реальную границу необходимо отодвинуть относительно своего действительного положения на величину ДL (рис. 4).

Для случая, когда расстояние от скважины до реки 200 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 2.

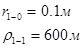
Используя полученные значения запишем систему (7) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

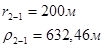
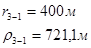
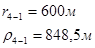
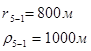
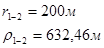
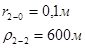
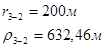
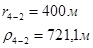
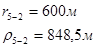
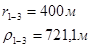
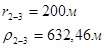
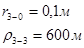
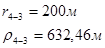
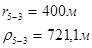
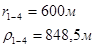
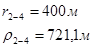
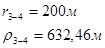
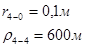
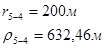
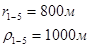
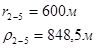
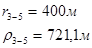
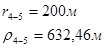
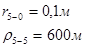
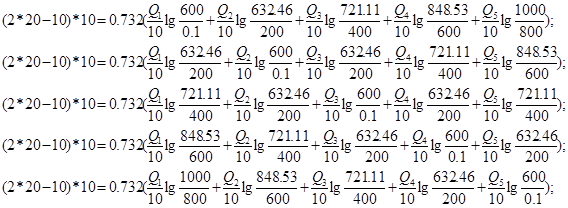
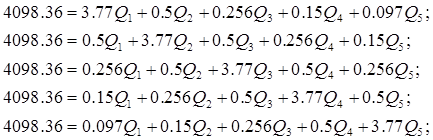
Решив систему с помощью Mathcad, имеем:

Q1= 878.079 м³/сут;

Q2= 781.76 м³/сут;

Q3= 760.484 м³/сут;

Q4= 781.76 м³/сут;

Q5= 878.079 м³/сут;

Qсум= 4080.162 м³/сут.

Для случая, когда расстояние от скважины до реки 500 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин.

Таблица 3

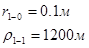
Используя полученные значения запишем систему (7) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

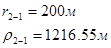
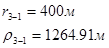
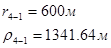
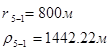
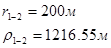
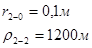
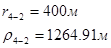
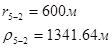
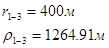
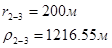
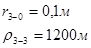
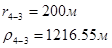
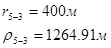
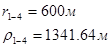
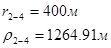
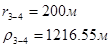
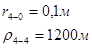
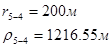
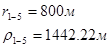
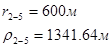
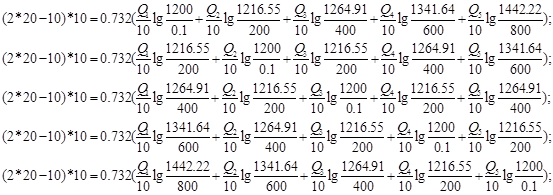
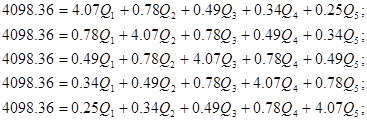
Решив систему с помощью Mathcad, имеем:

Q1=720.39 м³/сут;

Q2= 619.894 м³/сут;

Q3= 595.908 м³/сут;

Q4= 619.894 м³/сут;

Q5= 720.39 м³/сут;

Qсум= 3276.476 м³/сут.

Для случая, когда расстояние от скважины до реки 1000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 4.

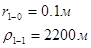
Используя полученные значения запишем систему (7) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

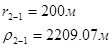
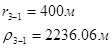
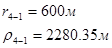
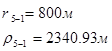
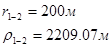
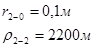
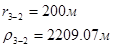
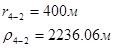
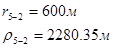
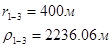
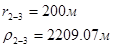
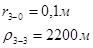
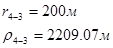
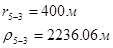
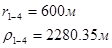
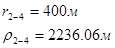
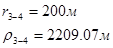
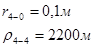
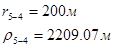
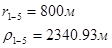
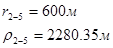
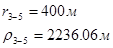
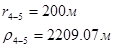
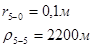
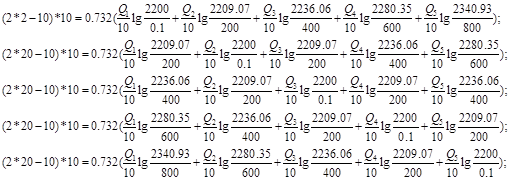
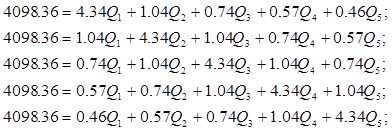
Решив систему с помощью Mathcad, имеем:

Q1=605.589 м³/сут;

Q2= 514.243 м³/сут;

Q3= 419.351 м³/сут;

Q4= 514.243 м³/сут;

Q5= 605.589 м³/сут;

Qсум= 2659.015 м³/сут.

Для случая, когда расстояние от скважины до реки 2000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 5.

Используя полученные значения запишем систему (7) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

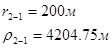
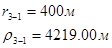
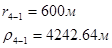
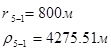
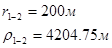
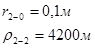
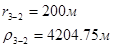
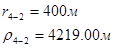
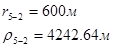
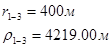
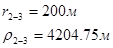
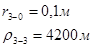
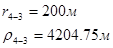
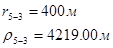
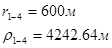
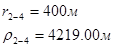
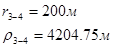
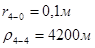
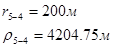
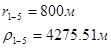
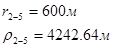
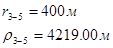
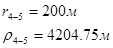
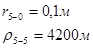
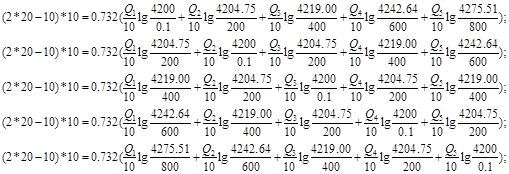
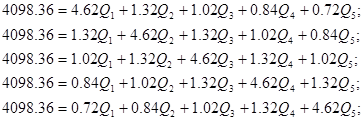
Решив систему с помощью Mathcad, имеем:

Q1=513.307 м³/сут;

Q2= 433.476 м³/сут;

Q3= 412.735 м³/сут;

Q4= 433.476 м³/сут;

Q5= 513.307 м³/сут;

Qсум= 2306.309 м³/сут.

Для случая, когда расстояние от скважины до реки 5000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин.

Таблица 6

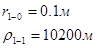
Используя полученные значения запишем систему (7) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

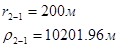
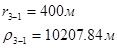
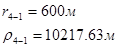
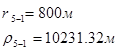
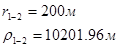
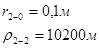
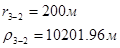
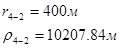
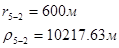
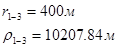
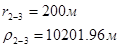
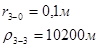
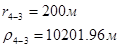
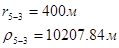
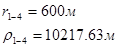
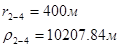
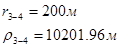
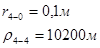
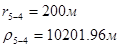
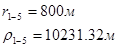
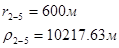
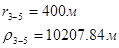
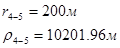
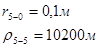
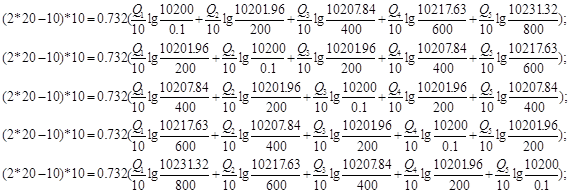
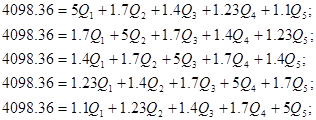
Решив систему с помощью Mathcad, имеем:

Q1=422.446 м³/сут;

Q2= 356.468 м³/сут;

Q3= 340.704 м³/сут;

Q4= 356.468 м³/сут;

Q5= 422.446 м³/сут;

Qсум= 1898.532 м³/сут.

Получив значения суммарного Qскв на различных расстояниях от реки, очевидно, что чем дальше от реки — тем меньше дебит скважин.

Решим аналогичную задачу для граничных условий ІІ-го рода. В этом случае параметр несовершенства гидравлической связи реки и водоносного горизонта не учитывается. Расчет дебитов скважин можем производить по следующей системе:

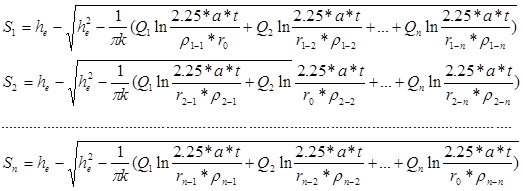
(8).

где: а — коэффициент уровнепроводности, м²/сут;

t — время, принимаемое 10 ⁴ сут;

hе — естественная мощность водоносного горизонта, м;

Sп — понижение уровня воды в скважине, м;

r — расстояние между скважинами, м;

с — расстояние от расчетной скважины до зеркально отображенной, м;

Qп — дебит п-ной скважины, м³/сут.

Для случая, когда расстояние от скважины до реки 200 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 7.

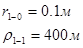
Используя полученные значения запишем систему (8) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

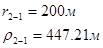
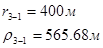
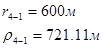
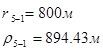
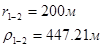
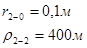
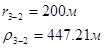
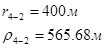
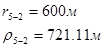
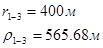
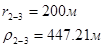
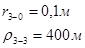
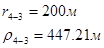
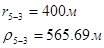
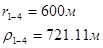
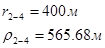
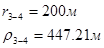
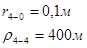
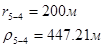
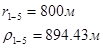
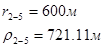
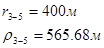
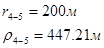
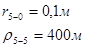
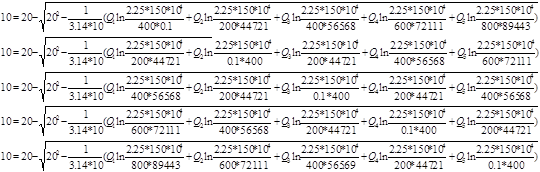
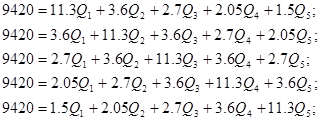
Решив систему с помощью Mathcad, имеем:

Q1=492.065 м³/сут;

Q2= 383.156 м³/сут;

Q3= 354.348 м³/сут;

Q4= 383.156 м³/сут; Q5= 492.065 м³/сут; Qсум= 2104.79 м³/сут.

Для случая, когда расстояние от скважины до реки 500 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 8.

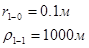
Используя полученные значения запишем систему (8) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

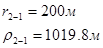
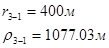
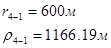
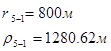
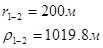
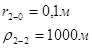
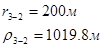
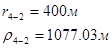
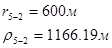
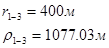
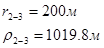
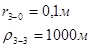
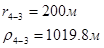
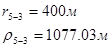
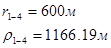
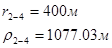
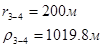
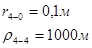
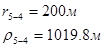
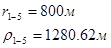
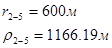
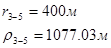
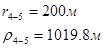
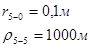
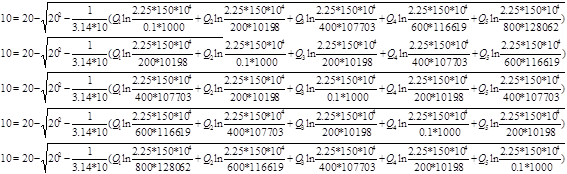
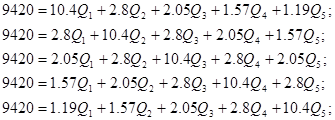
Решив систему с помощью Mathcad, имеем:

Q1=561.688 м³/сут;

Q2= 461.446 м³/сут;

Q3= 435.864 м³/сут;

Q4= 461.446 м³/сут;

Q5= 561.688 м³/сут;

Qсум= 2482.132 м³/сут.

Для случая, когда расстояние от скважины до реки 1000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин.

Таблица 9

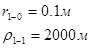
Используя полученные значения запишем систему (8) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

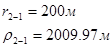
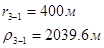
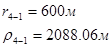
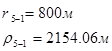
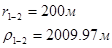
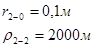
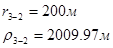
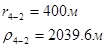
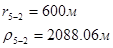
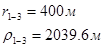
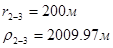
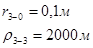
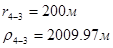
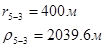
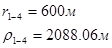
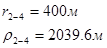
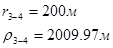
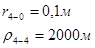
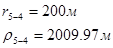
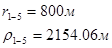
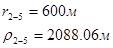
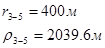
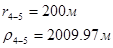
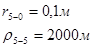
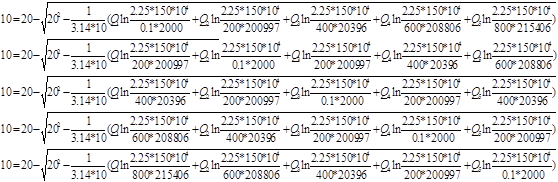
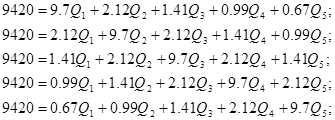
Решив систему с помощью Mathcad, имеем:

Q1=668.287 м³/сут;

Q2= 559.219 м³/сут;

Q3= 532.409 м³/сут;

Q4= 559.219 м³/сут;

Q5= 668.287 м³/сут;

Qсум= 2987.421 м³/сут.

Для случая, когда расстояние от скважины до реки 2000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 10.

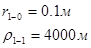
Используя полученные значения запишем систему (8) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

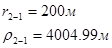
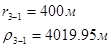
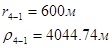
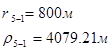
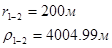
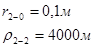
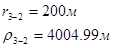
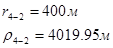
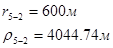
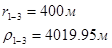
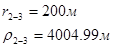
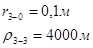
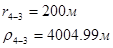
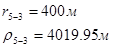
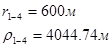
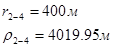
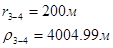
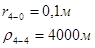
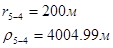
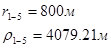
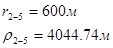
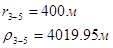
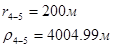
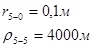
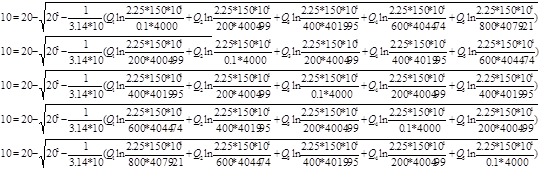
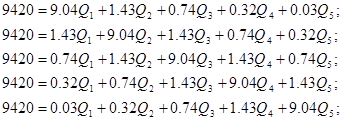
Решив систему с помощью Mathcad, имеем:

Q1=845.753 м³/сут;

Q2= 712.706 м³/сут;

Q3= 678.092 м³/сут;

Q4= 712.706 м³/сут;

Q5= 845.753 м³/сут;

Qсум= 3795.01 м³/сут.

Для случая, когда расстояние от скважины до реки 5000 м будем иметь:

Расстояния до реальных и зеркально отображенных скважин Таблица 11.

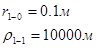
Используя полученные значения запишем систему (8) в следующем виде:

Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

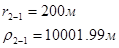
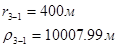
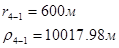
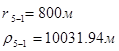
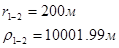
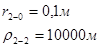
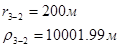
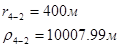
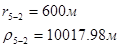
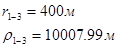
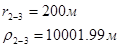
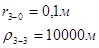
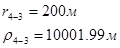
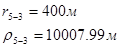
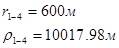
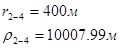
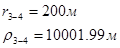
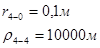
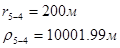
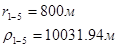
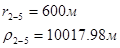
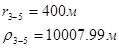
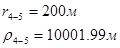
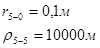
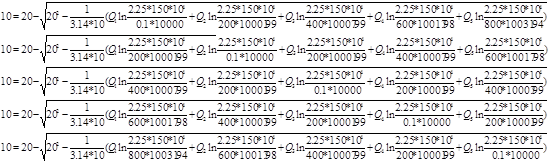
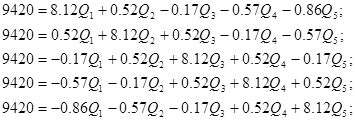
Решив систему с помощью Mathcad, имеем:

Q1=1330.35 м³/сут;

Q2= 1123.15 м³/сут;

Q3= 1072.95 м³/сут;

Q4= 1123.15 м³/сут;

Q5= 1330.35 м³/сут;

Qсум= 5979.95 м³/сут.

Сравнив полученные суммарные дебиты можно сделать вывод, что в водоносном горизонте с граничными условиями ІІ-го рода с увеличением расстояния от этой границы дебит скважин увеличивается, т. е. наблюдается прямая зависимость Qскв от расстояния от граничного условия.

В водоносном горизонте с граничными условиями І-го рода наблюдается обратная зависимость между Qскв и расстоянием от граничного условия, т. е. с увеличением расстояния Qскв уменьшается.

Решим аналогичную задачу для неограниченного пласта. Для этого необходимо решить следующую систему уравнений:

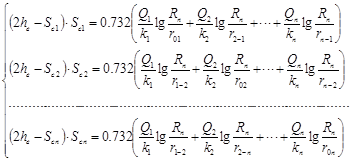
(9).

Как видно из системы (9) Qскв не зависит от расстояния до каких-либо ограничений.

Rп — приведенный радиус влияния скважин, который определяется по следующей формуле:

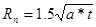
(10).

Приведенный радиус влияния скважин.

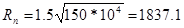
м Используя полученные значения запишем систему (9) в следующем виде:

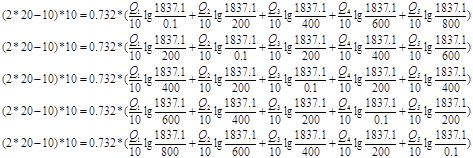
Упростим данную систему уравнений, приведем ее к системе из пяти уравнений:

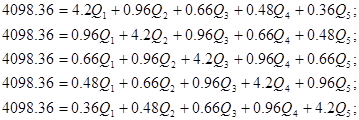
Решив систему с помощью Mathcad, имеем:

Q1=650.408 м³/сут;

Q2= 547.651 м³/сут;

Q3= 521.031 м³/сут;

Q4= 547.651 м³/сут;

Q5= 650.408 м³/сут;

Qсум= 2917.149 м³/сут.

Составим сводную таблицу зависимости дебета от расстояния до граничного условия. Зависимость Qскв от расстояния представлены в сводной таблице и на рис. 6.

Сводная таблица зависимости дебита от расстояния до граничных условий.

Таблица 12.

Построим график зависимости дебита от расстояния в зависимости от граничного условия.

• 1. Справочное руководство гидрогеолога В. М. Максимов, В. Д. Бабушкин, Н. Н. Веригин и др. — Л.: Недра, 1979. Т.И.-512 с.
• 2. Основы гидрогеологических расчетов / Ф. М. Бочевер, И. В. Гармонов, А. В. Лебедев, В. М. Шестаков. -М.: Недра, 1965. — 303 с.
• 3. Жернов И. Е. Динамика подземных вод.- Киев: Высшая шк. Главное изд., 1982. 324 с.