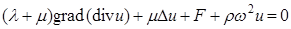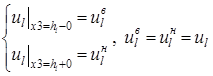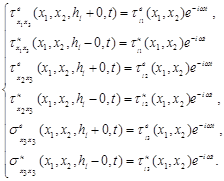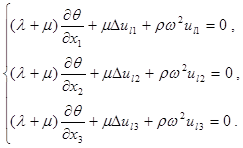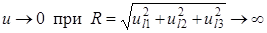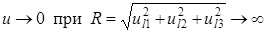Постановка задачи для пространства с внутренними плоскими включениями

Упругая изотропная среда содержит систему произвольного количества — N плоских включений, расположенных параллельно на высотах h₁,…, h_N соответственно (h₁ <�…< h_N). Включения занимают области ?_l с границами S_l, внешние нормали к границам, l=1,…, N.

Колебания упругой среды описываются уравнениями Ляме (1.1). Вектор перемещения точек среды в данном случае (x₁, x₂, x₃, t).

Дополнительные условия, налагаемые на рассматриваемые характеристики на границах заданных областей, приводят к краевым задачам. Упругая среда может быть пространством, полупространством или слоем. При этом на верхней границе могут быть заданы компоненты вектора перемещений или вектора напряжений .

Для установившихся колебаний:

(x₁, x₂, x₃, t) = (u₁, u₂, u₃)е^-iщt,.

уравнение Ляме (1.1) относительно комплексной амплитуды u примет вид:

. (2.2).

Для массива включений, на берегах неоднородностей заданы перемещения:

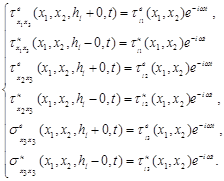
(2.3).

При этом напряжения среды в области включений терпят разрыв:

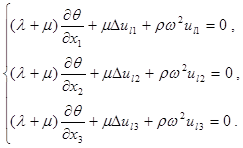
(2.4).

В покомпонентной записи уравнение (1.1) имеет вид:

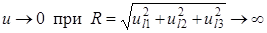
(2.5).

Для упругого пространства, содержащего плоские неоднородности, в качестве граничных условий берутся перемещения берегов включений:

l = 1,…, N (2.6).

и условия убывания на бесконечности.

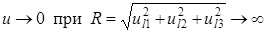
(2.7).

дополненные условиями излучения.

В качестве условий излучения выбраны следующие принципы.

• 1. Принцип Зоммерфельда: в решении удерживаются составляющие, описывающие волны, уходящие от источника в бесконечность, и отбрасываются те, скорость которых направлена к источнику.
• 2. Принцип предельного поглощения: в качестве решения задачи для идеально упругой среды берется равномерный по всем параметрам предел решения соответствующей задачи для вязкоупругой среды (среды с поглощением) при стремлении вязкости к нулю.

В данной работе исследовалась упругая задача для сред с включениями, напряженно-деформированное состояние которых определялось решением систем уравнений как относительно перемещений, так и относительно напряжений.