Обработка ведомости вычисления координат вершин теодолитного хода

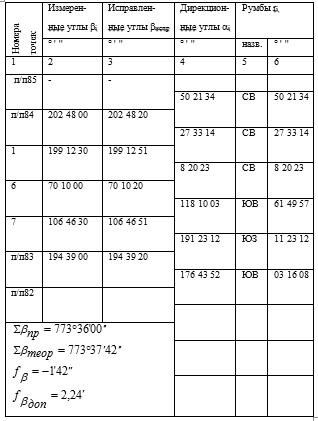
Обработка ведется в специальной ведомости (табл. 1.4) в следующей последовательности:

1. В графе 4 записывают исходный дирекционный угол начальной стороны бп/п85 — п/п84 и исходный дирекционный угол конечной стороны б п/п83 — п/п82.

Исходные дирекционные углы выделены жирным шрифтом. Для рассматриваемого примера;. Студент исходные данные своего варианта берет из задачи 1 подраздела 1.1.

2. Вычисляется сумма измеренных углов в ходе (значения измеренных углов записаны в графе 2) —. Для рассматриваемого примера .

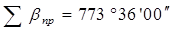
Если через и обозначим дирекционные углы в начале и конце теодолитного хода, которые заданы как неизменные и безошибочные, то в этом случае должно выполняться равенство.

(1.11).

где n — число вершин, на которых измерялись углы.

Если это равенство переписать для, то полученное выражение можно использовать для вычисления теоретической суммы углов в ходе. Отсюда.

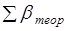
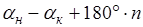
=. (1.12).

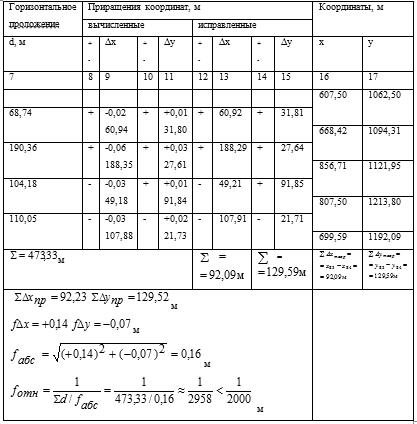
Таблица 1.4 Ведомость вычисления прямоугольных координат вершин теодолитного хода

Для рассматриваемого примера .

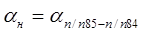
В нашем примере; .

Вследствие ошибок измерений углов практическая сумма измеренных горизонтальных углов не равна теоретической сумме горизонтальных углов, разность между ними называют угловой невязкой.

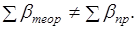
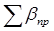
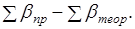
=(1.13).

Полученную невязку сравнивают с допустимой, которая вычисляется по формуле.

(1.14).

где n — число измеренных углов.

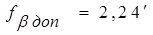
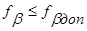
В нашем примере. Если выполняется неравенство, то делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:

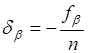
.(1.15).

Поправки вычисляются до целых секунд. Должно выполняться равенство. К измеренным углам прибавляют поправку со своим знаком, результат записывают в графу 3.

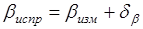
.(1.16).

Контролем правильности исправления углов служит равенство.

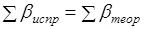
.(1.17).

После уравнивания углов вычисляют дирекционные углы всех сторон хода по формуле.

(1.18).

Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180є и минус правый (исправленный) угол хода, образованный этими сторонами.

Пример.

Для нашего хода вычисления ведут в следующей последовательности:

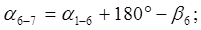
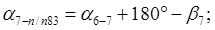
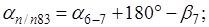
Вычисленный должен быть точно равен исходному. Результаты вычислений записывают в графу «Дирекционные углы» .

Если при вычислении дирекционный угол получается отрицательным, то кроме 180є к дирекционному углу предыдущей стороны необходимо прибавить 360є. Если дирекционный угол получается больше 360є, то из него вычитают 360є.

4. Производят уравнивание линейных измерений. Обработка линейных измерений начинается с вычисления приращений координат для всех сторон теодолитного хода по формулам

(1.19).

где d — горизонтальное проложение стороны хода; - дирекционный угол этой же стороны.

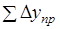
Вычисленные приращения координат (и) записывают в графы 9 и 11 табл. 1.4, находят их суммы, и приступают к их уравниванию.

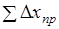
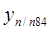
Зная координаты начальной точки и и приращения, можно вычислить координаты всех точек теодолитного хода:

; ;

; ;

; ;

;

.

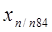
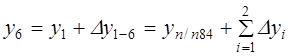
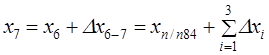
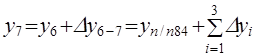
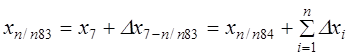
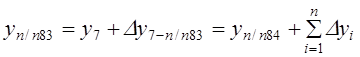
где п — число измеренных сторон хода.

Из последней строки системы определим и :

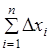
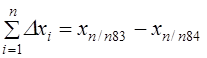
;. (1.20).

Или в общем виде; .

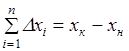
Эти формулы справедливы тогда, когда приращения координат не имеют погрешностей. Поэтому суммы данных приращений называют теоретическими и обозначают через и, т. е.

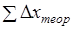
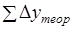
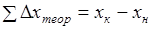
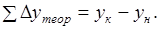
; (1.21).

Для нашего примера.

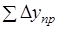
Так как измерения длин сторон имеют погрешности, то суммы вычисленных приращений (,) координат отличаются от теоретического значения. Разности этих величин называют невязками приращений.

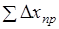
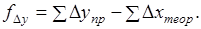
(1.22).

Невязки и показывают отклонение вычисленных координат конечной точки от её теоретического положения соответственно по осям и .

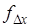
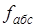
Для оценки точности используют линейную невязку, т. е. расстояние между этими точками (рис. 1.4). Линейную величину невязки определим как гипотенузу прямоугольного треугольника с катетами и .

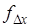
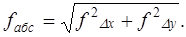
(1.23).

Наилучшим образом точность измерений в ходе характеризует относительная невязка, т. е. величина линейной невязки, отнесённая ко всему периметру полигона.

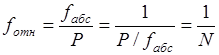
(1.24).

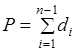
(1.25).

здесь п — число измерений сторон хода; Р — длина хода.

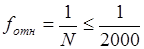
Относительную невязку принято записывать в виде дроби с единицей в числителе, что облегчает сравнение двух или нескольких значений. Качество измерений в теодолитном ходе считают удовлетворительным, если .

Если полученная относи-тельная невязка не превышает допустимого значения, то невязки и распределяют между приращениями координат.

Примеры в задании подобраны так, чтобы относительная невязка получилась допустимой. Если относительная невязка оказалась недопустимой, то в вычислениях допущены ошибки.

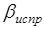
Дирекционные углы сторон хода вычислены по исправленным значениям горизонтальных углов. Следовательно, появление невязок вызвано погрешностями измерения длин сторон хода. Кроме того, погрешность измерения стороны хода пропорциональна её длине (т.е. чем больше длина стороны, тем большая вероятность появления погрешности в её измерении), поэтому невязки в приращениях координат распределяют пропорционально длинам сторон, для этого в каждое приращение вычисляют поправку по формулам.

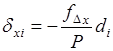
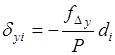
; .(1.26).

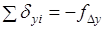
Контролем правильности распределения поправок являются равенства;. Далее вычисляют исправленные значения приращений координат.

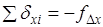
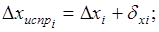
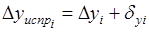
. (1.27).

Контролем вычислений служит выполнение равенства.

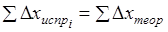
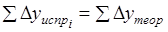
;. (1.28).

Для разомкнутого теодолитного хода.

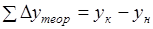
(1.29).

следовательно,.

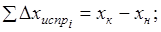
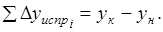
(1.30).

Вычисление координат точек теодолитного хода производят по формулам.

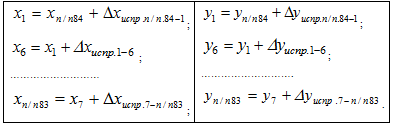
Получение x_п/п83 и y_п/п83, равных исходным значениям, служит контролем правильности вычисления координат точек теодолитного хода.