Методические основы изучения темы «Четырехугольники» в курсе геометрии

Изучение четырехугольников в курсе геометрии основной школы является разделом традиционным и достаточно важным во всех периодах школьного образования. В курсе геометрии 7−9-х классов данная тема является весьма актуальной, так как на рассмотренном материале, как на фундаменте, строят и изучают другие разделы геометрии: преобразование фигур, площади, многоугольники. Кроме того, изучение многогранников, площадей и объемов также базируется на этой теме.

Естественно, что учитель при подготовке к преподаванию этой темы должен четко себе представлять обобщенные цели и учебные задачи, которые ставятся при обучении теме «Четырехугольники», иметь перед собой карту изучения темы.

Рассмотрим задачи, изучаемые в школьном курсе геометрии по теме «Четырехугольники».

Задача 1: Доказать, что в любом четырёхугольнике какие-то две противоположные вершины лежат по разные стороны от прямой, проходящей через две другие вершины.

Решение: Если четырёхугольник ABCD выпуклый, то согласно теореме о свойстве диагоналей выпуклого четырёхугольника его диагонали АС и BD пересекаются и, следовательно, отрезок АС пересекается с прямой BD. Это и означает, что противоположные вершины, А и С лежат по разные стороны от прямой BD.

Пусть четырёхугольник ABCD невыпуклый и прямая АВ пересекает сторону CD в точке М. Возможны два случая:

Точка В лежит на отрезке AM. В этом случае точки, А и М лежат по разные стороны от прямой BD. Отрезок MC не пересекается с прямой BD, поэтому точка С лежит по ту же сторону от прямой BD, что и точка М. Итак, вершина, А лежит по одну сторону от прямой BD, а противоположная вершина С, по другую сторону от этой прямой.

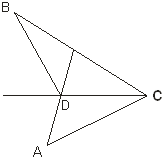
Точка, А лежит на отрезке BM. В этом случае, так же как и в случае 1), можно доказать, что противоположные вершины B и D лежат по разные стороны от прямой AC.

Задача 2: Диагонали четырехугольника ABCD пересекаются в точке P. Расстояние от точек A, B, и P до прямой CD равны a, b, и p. Докажите, что площадь четырехугольника ABCD равна.

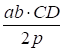
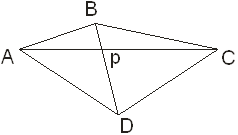
Решение: Пусть площади треугольников ABP, BPC, CPD и DPA и .

Тогда и, а.

значит,.Учитывая, что, получаем требуемое.

Задача 3: Четырёхугольник ABCD вписан в окружность радиуса R; -угол между его диагоналями. Докажите, что площадь S четырёхугольника ABCD равна 2R.

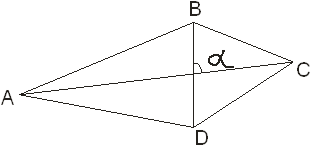
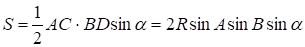
Решение: Применяя теорему синусов к треугольникам ABC и ABD, получаем AC=2RsinB и BD=2RsinA. Поэтому .

Задача 4: Докажите, что ломанная АОС делит ABCD на две фигуры равной площади.

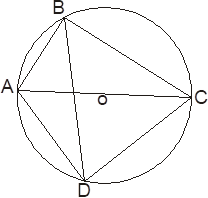
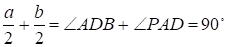
Решение: Пусть AOB=a и COD=b. Тогда. А так как и, где R-радиус описанной окружности, то. Аналогично .

Задача 5: Известен радиус описанной окружности R.

• 1) Найдите АР +ВР +СР +DP .
• 2) Найдите сумму квадратов сторон четырёхугольника ABCD.

Решение: Пусть AOB=2a и COD=2b. Тогда a+b=ADP=PAD=90.Поэтому. Аналогично,.

Задача 6: Найдите сумму квадратов диагоналей, если известны длина отрезка ОР и радиус окружности R.

Решение: Пусть М-середина АС, N-середина BD. AM =АО-ОМ, BN =ВОON, поэтому, так как .

Задача 7: Из вершин, А и В опущены перпендикуляры на CD, пересекающие прямые BD и АС в точках К и L соответственно. Докажите, что AKLB-ромб.

Решение: Острые углы BLP и ВDC имеют соответственно перпендикулярные стороны, поэтому они равны. Следовательно, BLP= BDC =ВАР. Кроме того, AKBL и ALBK. Поэтому AKLB-ромб.

Задача 8: Докажите, что площадь четырехугольника ABCD равна (AB*CD+BC*AD)/2.

Решение: Возьмём на описанной окружности точку так, что. Так как, то BD-диаметр, а значит, DAB=DCB=90. Поэтому .

Задача 9: Докажите, что расстояние от точки О до стороны АВ равно половине длины стороны CD.

Решение: Проведём диаметр АЕ. и, поэтому. Углы, опирающиеся на хорды ЕВ и CD, равны, поэтому EB=CD. Так как ЕАВ=90, расстояние от точки О до АВ равно ЕВ/2.

Задача 10: В четырехугольнике ABCD углы, А и В равны, а DC. Докажите, что тогда ADBC.

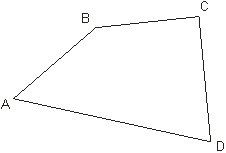
Решение: Пусть А=В. Достаточно доказать, что если ADBC, то DC. Возьмем на стороне BC точку так, что BD=AD. Тогдаравнобедренная трапеция. Поэтому D=C.

Задача 11: В трапеции ABCD при основании AD удовлетворяют неравенствам AD90. Докажите, что ACBD.

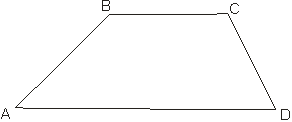
Решение: Пусть В' и C'-проекции точек В и С на основание AD. Так как BABCDC и BB=CC, то ABDC и поэтому BDAC. Следовательно, BD=BD+BBAC+CC=AC.

Задача 12: Докажите, что если два противоположных угла четырехугольника тупые, то диагональ, соединяющая вершины этих углов, короче другой диагонали.

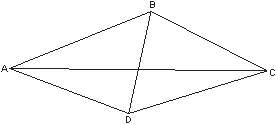
Решение: Пусть углы B и D четырехугольника ABCD тупые. Тогда точки В и D лежат внутри окружности с диаметром AC. Так как расстояние между любыми двумя точками, лежащими внутри окружности, меньше ее диаметра, то BDAC.

Задача 13: Докажите, что сумма расстояний от произвольной точки до трёх вершин равнобедренной трапеции больше расстояния от этой точки до четвёртой вершины.

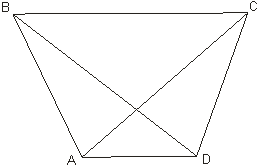
Решение: В равнобедренной трапеции ABCD диагонали AC и BD равны. Поэтому BM+(AM+CM).

Задача 14: Угол, А четырёхугольника ABCD тупой; F-середина стороны ВС. Докажите, что 2FA.

Решение: Пусть О-середина отрезка BD. Точка, А лежит внутри окружности с диаметром BD, поэтому OA.

Задача 15: Пусть М и N-середины сторон ВС и CD выпуклого четырёхугольника ABCD. Докажите, что.

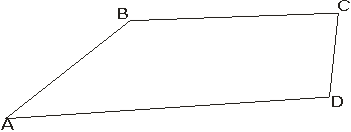
Решение: Ясно, что. Если отрезок AM пересекает диагональ BD в точке А, то S. Значит,.

Задача 16: Точка Р лежит внутри выпуклого четырёхугольника ABCD. Докажите, что сумма расстояний от точки Р до вершин четырёхугольника меньше суммы попарных расстояний между вершинами четырёхугольника.

Решение: Диагонали АС и BD пересекаются в точке О. Пусть для определённости точка Р лежит внутри треугольника AOB. Тогда AC+BD и CP+DPCB+BA+AD.

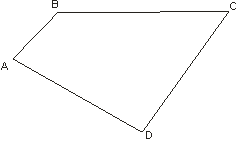
Задача 17: Докажите, что расстояние от одной из вершин выпуклого четырёхугольника до противоположной диагонали не превосходит половины этой диагонали.

Решение: Пусть AC<=BD. Опустим из вершин, А и С перпендикуляры АА и СС на диагональ BD. Тогда АА +СС <=AC<=BD, а значит, АА <=BD/2 или СС <=BD/2.

Задача 18: В трапеции ABCD (ADBC, ADBC) на диагонали AC взята точка E такая, что BECD. Доказать, что .

Решение:

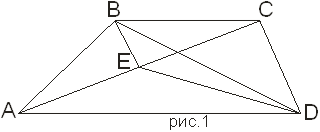
I способ. По условию BCDE-трапеция, поэтому (рис.1).

Аналогично, в трапеции ABCD имеем. Следовательно, .

II способ.

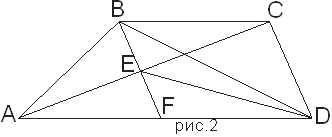
Продолжим прямую BE до пересечения с AD в точке F (рис. 2).

Тогда площадь каждого из треугольников ABC и DEC равна половине площади параллелограмма BCDF (общая сторона и высота). Следовательно, .

Задача 19: Докажите, что если центр вписанной в четырёхугольник окружности совпадает с точкой пересечения диагоналей, то этот четырёхугольник-ромб.

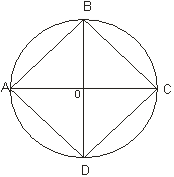
Решение: Пусть О-центр вписанной окружности и точка пересечения диагоналей четырёхугольника ABCD. ТогдаACB=ACD и BAC=CAD. Поэтому треугольники ABC и ADC равны, так как сторона АС у них общая. Следовательно, AB=DA. Аналогично AB=BC=CD=DA.

Задача 20: Четырёхугольник ABCD описан около окружности с центром О. Докажите, что АОВ+ СOD=180.

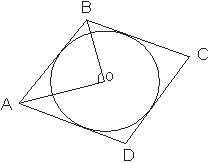
Решение: Ясно, что AOB=180-BAO-ABO=180(A+B)/2 и COD=180-(C+D)/2. Следовательно, AOB+COD=360-(A+B+C+D)/2=180.

Задача 21: Докажите, что если существует окружность, касающаяся продолжений всех сторон выпуклого четырёхугольника АВСВ, и окружность касающаяся продолжений всех его сторон, то диагонали такого четырехугольника перпендикулярны.

Решение: Рассмотрим две окружности, касающиеся сторон данного четырёхугольника и их продолжений. Прямые, содержащие стороны четырёхугольника, являются общими внутренними и внешними касательным" к этим окружностям. Прямая, соединяющая центры окружностей, содержит диагональ четырёхугольника, и, кроме того, она является осью симметрии четырёхугольника. Значит, вторая диагональ перпендикулярна этой прямой.

Задача 22: В трапеции ABCD (ADBC), Найти площадь трапеции ABCD.

Решение: Пусть h — высота трапеции. Заметим, что так как основание BC и высота h у них общее, тогда.

Задача 23: Диагонали параллелограмма равны 16 м и 12 м, а угол между ними равен 30. Найдите площадь параллелограмма.

Для произвольного четырехугольника верна формуладлина диагоналей, — угол между ними.

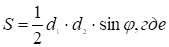
Тогда.

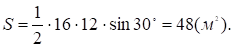
Задача 24: В параллелограмме ACBM AC=16 м, CB=24 м, CE и CF — соответственно высоты, проведенные к сторонам AM и BM, ECF=60. Найти длину высоты CE.

Решение: По условию в параллелограмме ACBM CEAM и ECF=60, тогда ACE=30. Значит,.

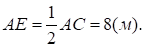
Из AEC, где AC=16 м, AE=8 м,.

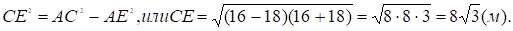
Задача 25: Основание трапеции a и b. Найти длину отрезка, соединяющего середины диагоналей.

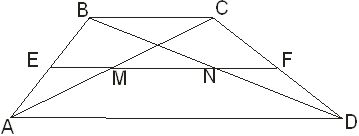
Решение: Так как по условию задачи точка M — середина диагонали AC и точка N — середина BD, то точки M и N лежат на средней линии трапеции EF. Так как EN — средняя линия ABD, то Аналогично, Значит,.