Исследование напряженно-деформированного состояния стержня при поперечном изгибе

Задание Для заданной упругой системы (рис. 1) исследовать напряженно-деформированное состояние при поперечном изгибе.

Исходная схема.

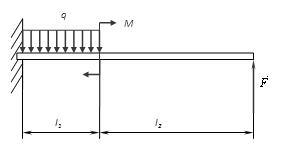
Рис. 1.

Исходные данные:

Длина первого участка стержня l1 = 1 м;

Длина второго участка стержня l2 = 2 м;

Сосредоточенная сила F= 3000 Н;

Сосредоточенный момент M = 6000 Н· м Интенсивность распределенной нагрузки, действующей на участке стержня длиной l1 q = 3000 H/м;

Поперечное сечение стержня прямоугольник со сторонами b и h:

• · ширина поперечного сечения b = 5 см = 0,05 м;
• · высота поперечного сечения h = 10 см = 0,1 м;

Предел текучести материала = 220 МПа;

Коэффициент запаса по пределу текучести = 2.

Цели и задачи работы.

• · изучить навыки работы в пакете инженерно-прикладных программ ANSYS 10.0/ED;
• · исследовать напряженно-деформированное состояние стержня при поперечном изгибе. Построить эпюры внутренних силовых факторов;

Оборудование и программное обеспечение:

Персональный компьютер;

Операционная система Windows. Пакет инженерно-прикладных программ ANSYS 10.0/ED.

Расчет стрежня в пакете инженерно-прикладных программ ANSYS 10.0/ED.

Построение конечной элементной модели стержня Устанавливаем систему единиц измерения СИ Вводим в командной строке /UNITS, SI.

Задаем тип конечного элемента Используя интерактивное меню пользователя, в окне препроцессора (Preprocessor) выбираем меню Еlements type, далее add / edit / delete /…, выбираем «добавить» (add), после чего в появившемся окне Library of Element Types выбираем необходимый элемент (твердотельный двумерный стержневой элемент с одной степенью свободы BEAM — 3D elastic 4).

Задаем опции элемента Используя интерактивное меню пользователя, в окне препроцессора (Preprocessor), выбираем меню Еlements type, далее add / edit / delete /…, выбираем Options, в появившемся окне BEAM 4 element type options в строке output at extra intermed pts K9 выбираем 9 intermed pts.

Задаем свойства материала (модуль Юнга первого рода и коэффициент Пуассона). Материал стержня считаем идеально упругим и изотропным Путь в меню:

Preprocessor> material props > material models > structural > linear > elastic > isotropic >

Далее в появившемся окне задаем модуль Юнга и коэффициент Пуассона:

• · EX=2E11 — модуль Юнга первого рода;
• · PRXY=0.3 — OK — коэффициент Пуассона.

Задаем постоянные элемента Задаем площадь поперечного сечения A = 0,01 м².

Путь в меню:

Preprocessor > real constants > add / edit / delete > add >

В появившемся окне задаем:

AREA = 0,001 — площадь поперечного сечения стерня;

IZZ = 0,208 — момент инерции поперечного сечения относительно оси z;

IYY = 0,33 — момент инерции поперечного сечения относительно оси y;

TKZ = 0,02 — ширина поперечного сечения по оси z;

TKY = 0,05 — ширина поперечного сечения по оси y;

IXX = 0,241 — полярный момент инерции поперечного сечения.

Задаем опорные точки (рис. 5).

Путь в меню:

Preprocessor > modeling create > keypoints > in active CS >

Далее вводим координаты опорных точек (точка 1 (0; 0), точка 2 (0; 1), точка 3 (0; 3)).

Рис. 5.

Рис. 6.

Генерируем опорные линии (рис. 6).

Путь в меню:

Preprocessor > modeling create > lines > straight line >

Указываем опорные точки (точки 1 и 2), являющиеся началом и концом первой линии. Аналогичным образом строим вторую линию, соединяя вторую и третью точки.

Задаем число конечных элементов на опорных линиях (рис. 7).

Путь в меню:

Preprocessor > meshing > size cntrls > picked lines >

Указываем нужную линию и вводим число конечных элементов.

Генерируем конечно-элементную модель стержня (рис. 8, рис. 9).

Путь в меню:

Preprocessor > meshing — mesh > lines >

Далее нажимаем кнопку pick all (генерировать элементы на всех линиях).

Рис. 7.

Рис. 8.

Задаем граничные условия Задаем условия закрепления Путь в меню:

Preprocessor >loads > loads apply > on keypoints > displacement >

Указываем точку 1. В появившемся окне нажимаем all dof (закрепляем все степени свободы).

Задаем условия нагружения.

Рис. 9.

Рис. 10.

Задаем сосредоточенный момент и силу (рис. 10).

Путь в меню:

Preprocessor > loads > loads apply > force/moment > on keypoints.

Указываем точку 2, в которой действует сосредоточенный момент M. В появившемся окне выбираем MZ и задаем значение момента — 3000. Аналогично задаем силу F, действующую в точке 4.

Задаем распределенную нагрузку (рис. 10):

· выбираем линию приложения распределенной нагрузки.

Путь в меню:

Utility Menu > Select > entities > lines.

Далее указываем линию 1, на которой действует распределенная нагрузка.

· Выбираем узлы, принадлежащие выбранной линии Путь в меню:

Select > entities > elements > attached to >

Выбираем все элементы, принадлежащие выделенной линии (нажимаем кнопку lines all);

· задаем распределенную нагрузку на всех элементах.

Путь в меню:

Preprocessor > loads > loads apply > Pressure > on Beams > pick all >

В диалог-окне:

1) задаем значение интенсивности распределенной нагрузки:

VALI 500;

VALJ 500;

2) задаем направление распределенной нагрузки LKEY 1;

выделяем все объекты Путь в меню:

Utility Menu > Select > everything.

Сохраним файл базы данных конечно-элементной модели закрепленного стержня с нагрузкой Путь в меню:

Utility Menu > File > Save as > Save DataBase >

В появившемся окне выбираем директорию, где необходимо сохранить файл базы данных, указываем тип файла и вводим его имя.

Запускаем программу на автоматизированный расчет Путь в меню;

Solution >Solve current LS >

Просмотр и анализ результатов расчета Строим эпюру поперечной силы Qy (рис. 11).

Вводим в командной строке:

ETABLE, MFORYI, SMISC, 2.

ETABLE, MFORYJ, SMISC, 62.

PLLS, MFORYI, MFORYJ.

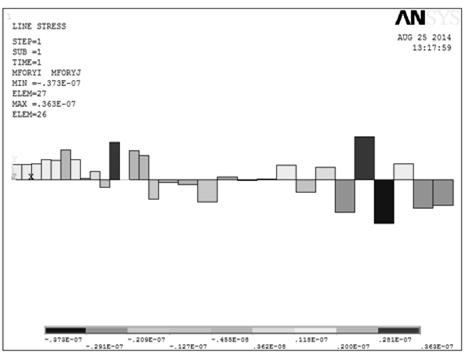
Рис. 11.

Строим эпюру изгибающего момента Mz (рис. 12).

Вводим в командной строке:

ETABLE, MMOMZI, SMISC, 6.

ETABLE, MMOMZJ, SMISC, 66.

PLLS, MMOMZI, MMOMZJ.

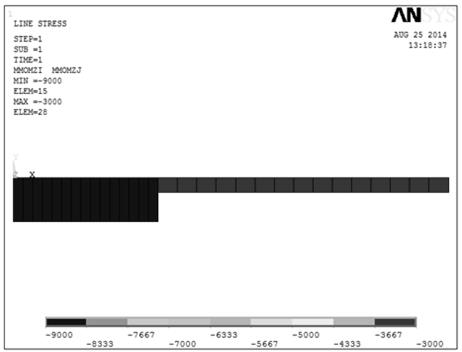
Рис. 12.

Сравниваем результаты расчета в пакете ANSYS 5.7/ED c результатами расчета методом сечений.

Изгибающий момент достигает максимального значения в поперечном сечении стержня на границе первого и второго силовых участков. По результатам ручного расчета установлено, что Mz на этом участке равен 2000 Н м.

Результаты расчета в пакете ANSYS 5.7/ED полностью соответствуют результатам ручного расчета (рис. 2, в и рис. 2, г). Для дальнейшего анализа можно использовать пакет ANSYS 5.7/ED.

Сохраним файл базы данных модели с результатами расчета.

Путь в меню:

Utility Menu > File > Save as > Save DataBase >

В появившемся окне выбираем директорию, где необходимо сохранить файл базы данных, указываем тип файла и вводим его имя.

Просмотрим распределение нормальных напряжений уx по длине (рис. 12) и по высоте балки в опасном сечении (рис. 14).

Рис. 13.

Рис. 14.

Определим допускаемые касательные напряжения по пределу текучести.

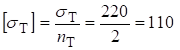
МПа.

Проведем проверку прочности по допускаемым напряжениям Сравним максимальные напряжения в стержне с допускаемыми напряжениями :

.

.

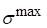
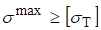
Условие прочности не выполняется. Требуется увеличение размеров поперечного сечения или уменьшение нагрузки.