Расчет доверительных интервалов, адекватность и точность моделей

Прогнозные значения исследуемого показателя определяют путем подстановки в уравнение кривой времени t, соответствующей периоду упреждения. Полученный прогноз называется точечным.

В дополнение к точечному прогнозу можно определить границы возможного изменения прогнозируемого показателя, т. е. вычислить интервальный прогноз.

Проверка адекватности модели.

Независимо от вида выбранной модели вопрос о возможности ее применения для прогнозирования экономического показателя может быть решен только после установления адекватности.

Проверка адекватности выбранных моделей реальному процессу строится на анализе случайной компоненты. Случайная компонента получается после выделения из исследуемого ряда тренда и периодической составляющей. сбыт спрос прогнозирование Считают, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойством случайности, независимости, и она подчиняется нормальному закону распределения.

При правильном выборе вида тренда отклонения от него будут носить случайный характер и изменения остаточной случайной величины не связано с изменением времени. По выборке, полученной для всех временных значений на рассматриваемом интервале, проверяется гипотеза о независимости последовательности значений et от времени или наличие тенденции в ее изменении. Для проверки этого свойства может быть использован критерий определения тенденции с помощью «восходящих и нисходящий» серий.

Если вид функции тренда выбран неудачно, то последовательные значения остатков ряда могут не обладать свойствами независимости, так как могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.

Наиболее распространенным примером обнаружения автокорреляции является метод Дарбина — Уотсона, связанный с автокорреляцией между соседними остаточными членами ряда. Определяется критерий ДарбинаУотсона по формуле:

В случае, когда в остатках имеется положительная автокорреляция, то при этом:

— если d < dl то гипотеза об отсутствии автокорреляции отвергается;

• -если d > d2, то гипотеза об отсутствии автокорреляции не отвергается;
• -если d1 < d < d2, то нет достаточных оснований для принятия решений.

Когда расчетное значение d > 2, то в etсуществует отрицательная автокорреляция и со значениями dx и d2 сравнивается величина d.

В связи с тем, что временные ряды экономических показателей невелики, на основе анализа показателей асимметрии и эксцесса можно произвести проверку ряда остатков на нормальность распределения по формуле:

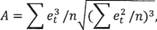
О точности модели можно судить по величине ошибки прогноза. Ошибка прогноза — величина, характеризующая разницу между фактическим и прогнозным значением показателя. Поскольку будущее никогда нельзя в точности предугадать по прошлому, то прогноз будущего спроса всегда будет содержать в себе ошибки в той или иной степени. Модель экспоненциального сглаживания прогнозирует средний уровень спроса. Поэтому следует построить модель так, чтобы уменьшить разность между прогнозом и фактическим уровнем спроса. Эта разность называется ошибкой прогнозирования.

Ошибка прогнозирования выражается такими показателями, как сред неквадратическое отклонение, вариация или среднее абсолютное отклонение. Раньше среднее абсолютное отклонение использовалось в качестве основного измерителя ошибки прогнозирования при использовании модели экспоненциального сглаживания. Среднеквадратическое отклонение отвергли из-за того, что рассчитывать его сложнее, чем среднее абсолютное отклонение, и у компьютеров на это просто не хватало памяти. Сейчас у компьютеров достаточно памяти, и теперь среднеквадратическое отклонение используется чаще.

Ошибку прогнозирования можно определить с помощью следующей формулы:

ОШИБКА ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС — ПРОГНОЗ СПРОСА Если прогноз спроса представляет собой среднее арифметическое фактического спроса, то сумма ошибок прогнозирования за определенное количество временных периодов будет равна нулю. Следовательно, значение ошибки можно отыскать путем суммирования квадратов ошибок прогнозирования, что позволяет избежать взаимного устранения положительных и отрицательных ошибок прогнозирования. Эта сумма делится на количество наблюдений и затем из нее извлекается квадратный корень. Показатель корректируется с уменьшением одной степени свободы, которая теряется при составлении прогноза. В результате, уравнение среднеквадратического отклонения имеет вид:

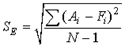
где SE — средняя ошибка прогнозирования;

Ai — фактический спрос в период i;

Fi — прогноз на период i;

N — размер временного ряда.

Форма распределения ошибок прогнозирования является важной, когда формулируются вероятностные утверждения о степени надежности прогноза.

Полагая, что модель прогнозирования отражает средние значения фактического спроса достаточно хорошо и отклонения фактических продаж от прогноза относительно невелики по сравнению с абсолютной величиной продаж, то вполне вероятно предположить нормальное распределение ошибок прогнозирования. В тех же случаях, когда ошибка прогнозирования сопоставима по величине с величиной спроса, имеет место скошенное, или усеченное нормальное распределение ошибок прогноза.

Одним из существенных преимуществ модели экспоненциального сглаживания при краткосрочном прогнозировании является возможность постоянной адаптации прогноза с учетом самых последних наблюдений во временном ряде. При этом точность прогнозирования напрямую зависит от значения сглаживающей константы в каждый конкретный период времени. Следовательно, усложненная процедура прогнозирования должна включать в себя регулярное отслеживание средней ошибки прогнозирования и соответствующую корректировку значения сглаживающей постоянной. Если временной ряд достаточно постоянный, то можно устанавливать низкие значения константы. В период больших колебаний спроса следует установить высокое значение константы. Но не следует ограничиваться каким-то одним значением, если изменение константы может привести к уменьшению ошибки прогнозирования, особенно в случае высокой динамики временного ряда.

Популярным методом отслеживания ошибки прогнозирования является метод усреднения отслеживающего сигнала. Отслеживающий сигнал — это результат сравнения, получаемого обычно в виде соотношения, текущий ошибки прогнозирования со средним значениям прошлых ошибок прогнозирования. В результате этого вычисления сглаживающая экспоненциальная константа может быть пересчитана или переопределена, если полученное соотношение превосходит ранее определенный контрольный уровень.

В целом, наилучшей сглаживающей константой является та, которая минимизирует ошибку прогнозирования так, как это было бы при стабильном временном ряде. Изменяя значение константы по мере т…

Если абсолютная и относительная ошибки больше нуля, то это свидетельствует о завышенной прогнозной оценке, если меньше нуля, то о заниженной.