Исследование операций.
Исследование операций

Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3, то есть (N— 1)=3. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, имеет… Читать ещё >
Исследование операций. Исследование операций (реферат, курсовая, диплом, контрольная)
Задача 1
Изложить теоретический материал по вопросу варианта. Проиллюстрировать теоретические положения числовыми примерами.
Методы теории массового обслуживания.
Практическая деятельность человека тесно связана с различного рода системами массового обслуживания. В области экономики — это банковское обслуживание, пользование объектами торговли и услугами сферы обслуживания и многие другие виды экономической деятельности.
Системы массового обслуживания (СМО) — это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания. Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.
Любая система массового обслуживания может включать в себя следующие элементы:
- 1. Входной поток требований или заявок на обслуживание. Этот элемент является основным. Изучение входящего потока требований и его описание необходимо при организации любой системы массового обслуживания.
- 2. Очередь. В тех случаях, когда поступающие в систему массового обслуживания требования не могут быть удовлетворены немедленно, возникает очередь. В такой ситуации интерес может представлять длина этой очереди, порядок, по которому ожидающие требования направляются на обслуживание (как говорят, дисциплина очереди), время ожидания.
В отдельных случаях систем массового обслуживания очереди не допускаются, т. е. требование, заставшее систему занятой, не обслуживается (получает отказ).
- 3. Обслуживающее устройство. Этот элемент присутствует в любой системе массового обслуживания. От характеристик и параметров, способов организации обслуживающего устройства зависит не только время, необходимое на обслуживание одного требования, но и длина очереди и время ожидания.
- 4. Выходной поток обслуженных требований. Этот элемент может оказаться очень важным в тех случаях, когда выходящий поток обслуженных требований является входящим для другой системы массового обслуживания.
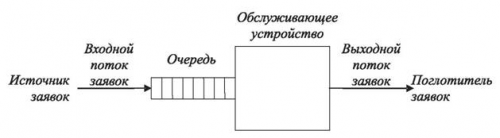
Рис. 1. Структура системы массового обслуживания
Как правило, число требований на входе системы массового обслуживания за какой-либо промежуток времени и время обслуживания одного требования являются случайными величинами.
Системы массового обслуживания классифицируются по разным признакам.
1. На группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дисциплины обслуживания требований.
По составу СМО бывают одноканальные (с одним обслуживающим устройством) и многоканальными (с большим числом обслуживающих устройств). Многоканальные системы могут состоять из обслуживающих устройств как одинаковой, так и разной производительности.
По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:
- 1) с неограниченным временем ожидания (с ожиданием),
- 2) с отказами;
- 3) смешанного типа.
В СМО с неограниченным временем ожидания очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.
В системах с отказами поступившее требование, застав все устройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.
В системах смешанного типа поступившее требование, застав все устройства занятыми, становятся в очередь и ожидают обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установленное время, требование покидает систему.
- 2. В системах с определенной дисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в очередь.
- 3. По числу каналов обслуживания СМО делятся на однои многоканальные.
- 4. По количеству этапов обслуживания различают однофазные и многофазные системы.
- 5. По месту нахождения источника требований СМО делятся на разомкнутые (источник требования вне системы) и замкнутые (источник в самой системе). Примером разомкнутой системы может служить ремонтная мастерская. Здесь неисправная техника — это источник требований, находящийся вне системы, число требований можно считать неограниченным. К замкнутым СМО относится, например, станочный участок, в котором станки являются источником неисправностей, а, следовательно, источником требований на их обслуживание, например, бригадой ремонтников.
Методы и модели исследования СМО можно условно разбить на аналитические и статистические.
Аналитические методы позволяют получить характеристики системы как некоторые функции от параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО.
Но, к сожалению, аналитические модели исследования операций зачастую не могут успешно применяться при принятии решений. Причина кроется в том, что математические модели, имеющие надежные методы вычисления, являются слишком упрощенными и неадекватны реальным процессам, либо не могут быть реализованы в силу вычислительных трудностей. В таком случае используется имитационное моделирование, которое состоит в компьютерном моделировании реальной производственной ситуации.
Но на сегодняшний день, для решения задач массового обслуживания, теоретически наиболее разработаны и удобны в практических приложениях методы решения, в которых поток требований является простейшим (пуассоновским). имитационный моделирование многоканальный Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t ровно k требований задается формулой.
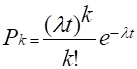
.
где л — параметр, интенсивность входящего потока заявок.
Простейший поток обладает тремя основными свойствами:
Ординарность — когда вероятность одновременного появления двух и более событий равна нулю.
Стационарность — когда вероятность попадания того или иного числа событий на участок времени, зависит только от длины этого участка.
Отсутствие последействий — когда вероятность не зависит от момента совершения предыдущих событий.
Важной характеристикой СМО является время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и, особенно в практических приложениях получил экспоненциальный закон распределения времени обслуживания.
Функция распределения для этого закона имеет вид.
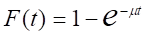
.
То есть вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой.
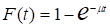
где м — параметр экспоненциального закона распределения времени обслуживания требований в системе (интенсивность обслуживания) — величина, обратная среднему времени обслуживания, то есть.
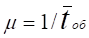
.
Теперь стоит привести некоторые аналитические модели исследования т расчета основных характеристик СМО.
Типичная постановка задачи, решаемой с помощью теории массового обслуживания, состоит в следующем: по заданному входящему потоку требований, известной дисциплине обслуживания и известному закону распределения времени обслуживания требования нужно оценить качество и эффективность функционирования СМО и выявить возможность их улучшения. Рассмотрим примеры:
1. Одноканальная СМО с отказами.
Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания для мойки автомобилей. Заявка — автомобиль, прибывший в момент, когда пост занят, — получает отказ в обслуживании. Интенсивность потока автомобилей л 1,0 (автомобиль в час). Средняя продолжительность обслуживания — tоб=1,8 часа.
Требуется определить в установившемся режиме предельные значения:
относительной пропускной способности q;
абсолютной пропускной способности А;
вероятности отказа Ротк;
Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва.
Решение Определим интенсивность потока обслуживания:
.
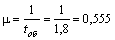
Вычислим относительную пропускную способность:
q =.
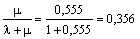
Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост автомобилей.
Абсолютную пропускную способность определим по формуле: А=лЧq=1Ч0,356=0,356.
Это означает, что система способна осуществить в среднем 0,356 обслуживания автомобилей в час.
Вероятность отказа:
Ротк=1-q=1−0,356=0,644.
Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании.
Определим номинальную пропускную способность системы:
Аном= (автомобилей в час).
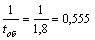
Оказывается, что Аном в раза больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.
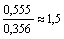
2. Одноканальная СМО с ожиданием и ограниченной очередью.
Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3, то есть (N— 1)=3. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, имеет интенсивность л=0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно =1,05 час.
Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Решение:
Интенсивность потока обслуживаний автомобилей:
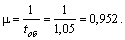
Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей л и м, т. е.
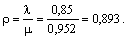
Вычислим вероятности нахождения п заявок в системе:
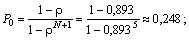
P1=r•P0=0,893•0,248=0,221;
P2=r2•P0=0,8932•0,248=0,198;
P3=r3•P0=0,8933•0,248=0,177;
P4=r4•P0=0,8934•0,248=0,158.
Вероятность отказа в обслуживании автомобиля:
Pотк=Р 4=r4•P0?0,158.
Относительная пропускная способность поста диагностики:
q=1-Pотк=1−0,158=0,842.
Абсолютная пропускная способность поста диагностики. А=л•q=0,85•0,842=0,716 (автомобиля в час).
Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):
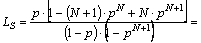
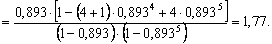
Среднее время пребывания автомобиля в системе:
часа.

Средняя продолжительность пребывания заявки в очереди на обслуживание:
Wq=Ws-1/м=2,473−1/0,952=1,423 часа.
Среднее число заявок в очереди (длина очереди):
Lq=л•(1-PN)•Wq=0,85•(1−0,158)•1,423=1,02.
Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обнаруживает автомобили в среднем в 15,8% случаев (Ротк=0,158).
3. Одноканальная СМО с ожиданием и неограниченной очередью.
Вспомнив о ситуации, рассмотренной в предыдущем примере, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченным количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.
Требуется определить финальные значения следующих вероятностных характеристик:
- 1. вероятности состояний системы (поста диагностики);
- 2. среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
- 3. среднюю продолжительность пребывания автомобиля в системе
- 4. (на обслуживании и в очереди);
- 5. среднее число автомобилей в очереди на обслуживании;
- 6. среднюю продолжительность пребывания автомобиля в очереди.
Решение
Параметр потока обслуживания и приведенная интенсивность потока автомобилей с определены в предыдущем примере:
м=0,952; с=0,893.
Вычислим предельные вероятности системы по формулам.
P0=1-r=1−0,893=0,107;
P1=(1-r)· r=(1−0,893)·0,893=0,096;
P2=(1-r)· r2=(1−0,893)·0,8932=0,085;
P3=(1-r)· r3=(1−0,893)·0,8933=0,076;
P4=(1-r)· r4=(1−0,893)·0,8934=0,068;
P5=(1-r)· r5=(1−0,893)·0,8935=0,061 и т. д.
Следует отметить, что Р 0 определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаивает). В нашем примере она составляет 10, 7%, так как Р 0=0,107.
Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):
ед.

Средняя продолжительность пребывания клиента в системе:
час.

Среднее число автомобилей в очереди на обслуживание:
.
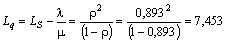
Средняя продолжительность пребывания автомобиля в очереди:
час.
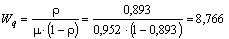
Относительная пропускаемая способность системы равна единицы, так как все поступившие заявки рано или поздно будут обслужены:
q=1.
Абсолютная пропускная способность:
A=л•q=0,85•1=0,85.
Следует отметить, что предприятие, осуществляющее диагностику автомобилей, прежде всего, интересует количество клиентов, которое посетит пост диагностики при снятии ограничения на длину очереди.
Допустим, в первоначальном варианте количество мест для стоянки прибывших автомобилей как в предыдущем примере было равно трем. Частота m возникновения ситуаций, когда прибывающий на пост диагностике автомобиль не имеет возможности присоединить к очереди:
m=л•PN.
В нашем примере при N=3+1=4 и r=0,893,.
m=л•P0•.
r4=0,85•0,248•0,8934=0,134 автомобиля в час.
При 12-часовом режиме работы поста диагностики это эквивалентно тому, что пост диагностики в среднем за смену (день) будет терять 12•0,134=1,6 автомобиля.
Снятие ограничения на длину очереди позволяет увеличить количество обслуживающих клиентов в нашем примере в среднем на 1,6 автомобиля за смену (12 ч. работы) пост диагностики.
Ясно, что решение относительно расширения площади для стоянки автомобиля, прибывающих на пост диагностики, должно основываться на оценке экономического ущерба, который обусловлен потерей клиентов при наличии всего трех мест для стоянки этих автомобилей.
4. Многоканальная СМО с отказами Примером является задание № 4.
5. Многоканальная СМО с ожиданием Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации.
Поток неисправных механизмов, прибывающих в мастерскую, — пуассоновский и имеет интенсивность л=2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательному закону и равно tоб=0,5 сут.
Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно.
Требуется вычислить следующие предельные значения вероятностных характеристик системы:
- — вероятность состояний системы;
- — среднее число заявок в очереди на обслуживание;
- — среднее число находящихся в системе заявок;
- — среднюю продолжительность пребывания заявки в очереди;
- — среднюю продолжительность пребывания заявки в системе.
Решение
Определим параметр потока обслуживаний.
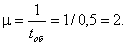
Приведенная интенсивность потока заявок с=л/м=2,5/2,0=1,25,.
при этом.
л/м •с=2,5/2•3=0,41<1.
Поскольку л/м•с<1, то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.
Вычислим вероятности состояний системы:
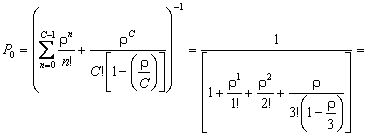
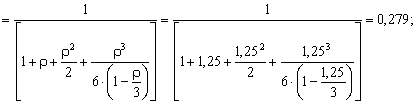
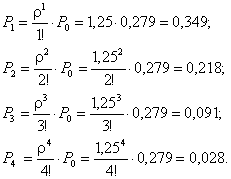
Вероятность отсутствия очереди у мастерской Ротк?Р 0+Р 1+Р 2+Р 3?0,279+0,394+0,218+0,091=0,937.
Среднее число заявок в очереди на обслуживание.
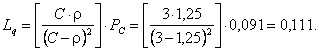
Среднее число находящихся в системе заявок.
Ls=Lq+=0,111+1,25=1,361.
Средняя продолжительность пребывания механизма в очереди на обслуживание суток.

Средняя продолжительность пребывания механизма в мастерской (в системе) суток.
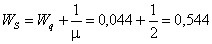
Задача 2.
Задание 1. Сформулировать экономико-математическую модель исходной экономической задачи.
Задание 2. Решить полученную задачу линейного программирования графическим методом.
Задание 3. Сформулировать двойственную задачу и найти ее оптимальное решение, используя теоремы двойственности.
Постановка задачи. В мастерской освоили производство столов и тумбочек для торговой сети из древесины видов 1 и 2. Имеется 72 куб. м древесины вида 1 и 56 куб м древесины вида 2, при этом на производство одного стола требуется 0,18 куб м древесины вида 1 и 0,08 куб м древесины вида 2, а на производство одной тумбочки уходит соответственно 0,09 куб. м и 0,28 куб. м видов древесины 1 и 2. От производства одного стола мастерская получает прибыль в размере 1,1 ден. Единиц, а одной тумбочки — 0,7 ден. Единиц. Сколько столов и тумбочек должна изготовить мастерская из имеющегося материала, чтобы получить наибольшую прибыль?
Для решения задачи приведем все вышеперечисленные величины в таблицу:Вид древесины. | Продукция. | Норма расхода, куб м/шт. | Объемы запасов, куб. м. |
Стулья. | Тумбочки. | ||
Др.1. | 0,18. | 0,09. | |
Др.2. | 0,08. | 0,28. | |
Прибыль от продажи, ден. ед. | 1,1. | 0,7. | ; |
1. Разработка ЭММ. Введем необходимые обозначения. Пусть:
x1 — количество столов, которое необходимо произвести для получения максимальной прибыли (шт.).
x2 — количество тумбочек, которое необходимо произвести для получения максимальной прибыли (шт.).
С учетом этих обозначений ЭММ рассматриваемой задачи имеет вид:
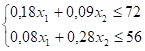
Целевая функция в данной задаче отражает критерий «оптимальности» — получение максимальной прибыли от реализации готовой продукции.
Первое функциональное ограничение — ограничение по запасам древесины 1-го вида.
Второе функциональное ограничение — ограничение по запасам древесины 2-го вида.
2. Реализация ЭММ.
Полученная ЭММ — задача линейного программирования Решим полученную задачу линейного программирования графическим методом.
a) Построим ОДР нашей задачи. Поскольку переменные x1 и x2 неотрицательны, то ОДР находится в I-ой четверти прямоугольной системы координат. Область определения первого ограничения-неравенства находится в нижней полуплоскости с границей, задаваемой уравнением. Областью определения второго ограничения-неравенства является нижняя полуплоскость с границей, определяемой уравнением .
Пересечение этих нижних плоскостей в I-ой четверти прямоугольной системы координат определяет многоугольник OABC — это и есть область допустимых решений нашей задачи.
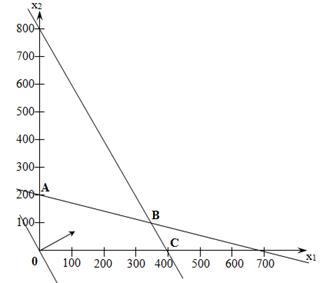
b) Определяем вектор-Градиент: .
c) Построим линию уровня. .
d) При перемещении линии уровня в направлении вектора-Градиента получаем предельную точку — точку B. Это и есть точка максимум, найдем ее координаты.
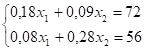
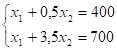
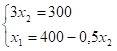
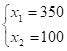
;;; .
Значение целевой функции в этой точке равно:
Сформулируем и решим двойственную задачу, используя теоремы двойственности.
Предположим, что мастерская решила приобрести древесину видов 1 и 2 и необходимо выбрать оптимальные цены на нее. Очевидно, что мастерская заинтересована в том, чтобы затраты на покупку древесины были минимальны. С другой стороны, предприятие, продающее древесину (например, деревообрабатывающий завод), заинтересовано в том, чтобы полученная выручка от продажи была не менее той суммы, которую предприятие может получить при изготовлении столов и тумбочек.
Таким образом, можно составить следующую двойственную задачу для нашей исходной задачи:
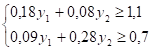
Поскольку в оптимальном плане исходной задачи, т. е., то по теореме о дополняющей нежесткости для двойственных оценок и имеет место равенство:
; ;

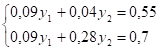
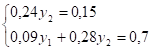
Из этой системы получаем двойственные оценки:
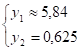
.
Двойственные оценки найдены правильно, т.к. для оптимальных планов двойственных задач имеет место первая теорема двойственности:
Ответ: 1. ЭММ задачи:
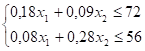
- 2. В рассматриваемой хозяйственной ситуации с позиции критерия «Максимум прибыли от реализации готовой продукции» следует изготавливать столов в объеме 350 шт. и тумбочек в объеме 100 шт. При таком плане производства ожидается максимальная выручка 455 ден. ед.
- 3. Двойственная задача имеет вид:
Двойственные оценки равны:
Задача 3
Найти наибольшее значение функции.
при ограничениях:
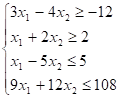
Решение данной задачи проведено средствами Excel в 3 этапа.
На I этапе создан рабочий лист Excel:
- Ш определены изменяемые ячейки (B2;C2),
- Ш целевая ячейка (E3),
- Ш ячейки функций (D5;D6; D7; D8).
Для создания целевой ячейки и ячеек функций использовалась стандартная функция Excel — СУММПРОИЗВ.
На II этапе вызываем программу оптимизации и оформляем окно диалога «Поиск решения» .
В режиме параметры окна диалога «Поиск решения» мы определяем тип задачи — линейная.
На III этапе оптимизируем результаты с помощью окна «Результаты поиска решения» .
Ответ: получено оптимальное решение: оптимальное значение, .
Максимальное значение целевой функции 26.
Задача 4
Задание 1. Записать исходные данные задачи в виде транспортной таблицы, определить, открытой или закрытой является транспортная задача.
Задание 2. Сформулировать экономико-математическую модель исходной транспортной задачи.
Задание 3. Найти оптимальный план перевозок.
Постановка задачи. Четыре сталелитейных завода Z1, Z2, Z3 и Z4 производят еженедельно 950, 300, 1350 и 450 т стали соответственно. Потребителям A, B, C и D еженедельно нужно 250, 1000, 700 и 1100 т стали, а стоимости перевозок 1 т стали с заводов потребителям для завода Z1 равны 12, 16, 21 и 19 ден. единиц, для завода Z2 — 4, 4, 9 и 5ден. единиц, для завода Z3 — 3, 8, 14 и 10 ден. единиц, а для завода Z4 — 24, 33, 36 и 34 ден. единиц соответственно. Составить план транспортировки стали с заводов потребителям, чтобы минимизировать общую стоимость перевозок.
Для решения задачи приведем все вышеперечисленные величины в таблицу:
Поставщики. | Потребители. | A. | B. | C. | D. | Запасы стали, т. |
Z1. | ||||||
Z2. | ||||||
Z3. | ||||||
Z4. | ||||||
Потребности, т. |
Рассматриваемая транспортная задача закрытая, т.к. выполняется уравнение баланса.
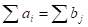
ЭММ транспортной задачи.
Введем необходимые обозначения: пусть xij (i = 1, 2, 3, 4; j = 1, 2, 3, 4) — объем перевозок от i-го поставщика к j-му потребителю.
Таким образом, план перевозок формально представляется матрицей перевозок:X=. |
С учетом этих обозначений ЭММ задачи имеет вид.
Критерий оптимальности — «минимум общей стоимости перевозок» .
ЦФ:
.
Ограничения по запасам поставщиков: Ограничения по потребностям:
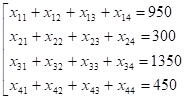
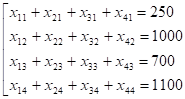
Решим задачу средствами Excel.
На I этапе создан рабочий лист Excel:
- Ш определены изменяемые ячейки (B2;E5),
- Ш целевая ячейка (H11),
- Ш ячейки функций (F2:F5; B6: E6).
Для создания целевой ячейки использовалась стандартная функция Excel — СУММПРОИЗВ.
Для создания ячеек функций использовалась функция СУММ На II этапе вызываем программу оптимизации и оформляем окно диалога «Поиск решения» .
В режиме параметры окна диалога «Поиск решения» мы определяем тип задачи — линейная.
Ответ: для минимизации общей стоимости перевозок необходимо, чтобы:
завод Z1 поставил сталь для потребителей B и C в количестве 450 т. и 500 т. соответственно;
завод Z2 — для потребителя D в количестве 300 т. стали;
завод Z3 — для потребителей B и D в количестве 550 т. и 800 т. соответственно;
завод Z4 — для потребителей A и C в количестве 250 т. и 200 т. соответственно.
При этом стоимость перевозок будет равна 44 800 ден. единиц.
Список используемой литературы
- 1. Методы оптимальных решений в экономике и финансах: учебник / И. А. Александрова [и др.]; под ред. В. М. Гончаренко, В. Ю. Попова. М.: Кнорус, 2013 .
- 2. Гармаш А. Н., Орлова И. В. Математические методы в управлении: учебное пособие. — М.: Вузовский учебник, 2012.
- 3. Исследование операций в экономике / под ред. Н. Ш. Кремера. — 2-е изд. — М.: Юрайт-издат: Высшее образование, 2010.
- 4. Колемаев В. А. Математические методы и модели исследования операций. Учебник. М.: ЮНИТИ, 2008.
- 5. Математика в экономике. Ч.1: Линейная алгебра, аналитическая геометрия и линейное программирование: Учебник / А. С. Солодовников, В. А. Бабайцев, А. В. Браилов, И. Г. Шандра. — 3-е изд., перераб. и доп. — М.: Финансы и статистика; ИНФРА-М, 2011 .
- 6. Афанасьев М. Ю., Багриновский К. А., Матюшок В. М. Прикладные задачи исследования операций: учебное пособие. — М.: ИНФРА-М, 2006.14
- 7. Афанасьев М. Ю., Суворов Б. П. Исследование операций в экономике: модели, задачи, решения: учебное пособие — М.: ИНФРА-М, 2003.
- 8. Мур Дж., Уэдерфорд Л. Экономическое моделирование в Microsoft Excel. — М.: ИД «Вильямс», 2004.
- 9. Орлова И. В., Половников В. А. Экономико-математические методы и модели: компьютерное моделирование: учебное пособие. — М.: Вузовский учебник, 2011.
- 10. Орлова И. В. Экономико-математическое моделирование: практическое пособие по решению задач. — 2-е изд. — М.: Вузовский учебник, 2012.