Сведение общей системы дифференциальных уравнений к нормальной

Здесь мы покажем, что весьма общая система дифференциальных уравнений сводится к нормальной системе и следовательно, для таких систем будет установлена теорема существования и единственности.

Сначала дадим описание общих систем дифференциальных уравнений.

В случае одной неизвестной функции x независимого переменного t дифференциальное уравнение n-го порядка имеет вид:

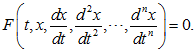
Здесь F — заданная функция от (n+2) переменных. Функция F, вообще говоря, может быть задана не при всех значениях своих аргументов и поэтому говорят об области D задания функции F. Предполагается обычно, что D — открытое множество евклидова пространства размерности n+2, координатами точек в котором являются переменные .

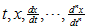
Максимальный порядок производной, входящей в данное дифференциальное уравнение, называется порядком этого уравнения. Решением уравнения (1.42)называется такая непрерывная функция x =??(t) переменного t, определенная на некотором интервале r₁ < t < r₂, которая обладает свойствами:

• — функция ?(t) обладает в интервале r₁ < t < r₂ непрерывными производными до порядка n включительно;
• — для всех t? (r₁, r₂);

— при подстановке x =??(t) в соотношение (1.42) мы получаем тождество по t на интервале r₁ < t < r₂.

Если имеются две неизвестные функции x и y одного переменного t, то рассматриваются два дифференциальных уравнения, вместе образующих систему уравнений. В общем случае эта система имеет вид:

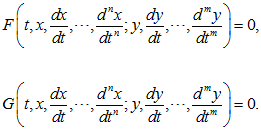
Здесь F и G — две функции, зависящие от n+m+3 переменных, определенные на некотором открытом множестве D евклидова пространства размерности n+m+3. Множество D называют областью задания системы (1.43). Если максимальный порядок производной функции x, входящей в систему (1.43) (точнее говоря, хотя бы в одно из уравнений системы (1.43)) равен n, а максимальный порядок производной функции y, входящей в систему (1.43), равен m, то число n называют порядком системы относительно функции x, а m — порядком системы относительно y. Число n+m при этом называют порядком системы (1.43). Аналогично предыдущему случаю не составляет труда сформулировать определение решения системы (1.43), а также дать определение системы дифференциальных уравнений для произвольного конечного числа неизвестных функций x₁,?, x_n от одного независимого переменного t. Если наивысший порядок производной функции x_i, входящей в систему, равен q_i, то число q_i называется порядком этой системы относительно функции x_i, а число q₁ +???+ q_n = q — порядком системы.

Предположим, что из соотношения (1.42) величина может быть представлена в виде однозначной функции остальных аргументов, то есть уравнение (1.42)равносильно следующему.

Уравнения (1.44) называются разрешенными относительно старшей производной.

Точно также система (1.43), разрешенная относительно старших производных, имеет вид:

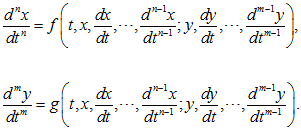
Аналогично определяются разрешенные относительно старших производных системы с произвольным числом неизвестных функций.

Покажем, что всякая система дифференциальных уравнений порядка n, разрешенная относительно старших производных, сводится к (эквивалентной ей) нормальной системе n-го порядка.

Все выкладки мы проведем для одного уравнения порядка n. Из этих выкладок легко понять процедуру сведения и для системы с произвольным (конечным) числом искомых функций.

Итак, пусть.

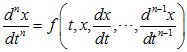
— одно дифференциальное уравнение порядка n, разрешенное относительно высшей производной. Предположим, что функция определена на некотором открытом множестве D (n+1)-го координатного пространства, непрерывна на D и удовлетворяет условию Липшица (равномерно по t) относительно переменных. Введем новые неизвестные функции y₁, y₂,?, y_n независимого переменного t по формулам:

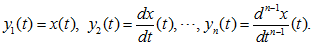
Если x =??(t) -решение уравнения (1.46) с интервалом определения r₁ < t < r₂, то из соотношений (1.47) следует, что вектор-функция y (t) = (y₁(t),?,y_n(t)) является непрерывно-дифференцируемой на интервале r₁ < t < r₂; точки (t,y(t)) = (t,y₁(t),?,y_n(t)) принадлежат множеству D при всех значениях t? (r₁,r₂) и при этом имеют место тождества: (по t? (r₁, r₂)).

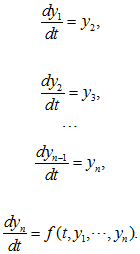
Другими словами, функции y₁(t),?,y_n(t) являются решением системы уравнений (1.48) нормального вида.

Обратно, пусть система функций y₁(t),?,y_n(t), определенных на интервале r₁ < t < r₂, является решением системы уравнений (1.48). Из непрерывной дифференцируемости функций y_i(t), i=1,?,n и первых (n?1) соотношений в (1.48) вытекает, что функция.

x(t)? y₁(t).

обладает на интервале r₁ < t < r₂ непрерывными производными до порядка n включительно и при этом справедливы тождества:

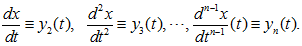
Следовательно, точки.

принадлежат D, при любом t из (r₁, r₂), а из последнего уравнения системы (1.48) вытекает тождество:

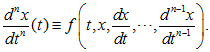
Другими словами, функция (1.49) является решением уравнения n-го порядка (1.46). В силу теоремы 1.3.1 существует и притом единственное решение системы (1.48) для любых начальных значений. Из формул (1.47) тогда следует, что функция (1.49), т. е. x(t) = y₁(t), доставляет единственное решение уравнения (1.46), удовлетворяющее начальным условиям:

Именно таким образом следует задавать начальные условия для уравнения вида (1.46). Задачу отыскания решения уравнения (1.46), удовлетворяющего дополнительным условиям (1.51), называют задачей Коши для этого уравнения.

Пример. Рассмотрим уравнение.

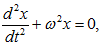
относящиеся к уравнениям второго порядка, разрешенным относительно старшей производной. Областью задания уравнения (1.52) является вся плоскость переменных (t,x). Непосредственной подстановкой проверяется, что функции удовлетворяют уравнению (1.52). Здесь r,?? — произвольные постоянные. Покажем, что функции (1.53) исчерпывают всю совокупность решений уравнения (1.52). Действительно, пусть x =??(t) — произвольное решение этого уравнения. В силу теоремы 1.3.2 можно считать, что решение ?(t) = x определено для всех значений t. Положим Не трудно убедиться, что постоянные r? 0 и ? можно выбрать так, чтобы имели место равенства Таким образом, решения (1.53) и ?(t) имеют одинаковые начальные значения и поэтому совпадают при всех t.

Функция (1.53) описывает гармонический колебательный процесс. Положительная константа r называется амплитудой колебания (1.53), а ? — его фазой (точнее начальной фазой). Уравнение (1.52) называется уравнением гармонических колебаний. Число ? называют частотой колебаний, хотя в действительности число ?колебаний в секунду равно.

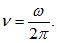
дифференциальный уравнение интегральный кривая.