Лекция 2. Кинематика твердого тела

Абсолютно твердым телом или неизменяемой системой называется механическая система, расстояния между точками которой неизменны при любых движениях.

Основными задачами кинематики твердого тела являются:

• А) Задача задания движения тела.
• Б) Задача определения кинематических характеристик твердого тела — угловой скорости и углового ускорения тела.
• В) Задача определения кинематических характеристик отдельных точек тела — задача распределения скоростей и ускорений.

Первая задача кинематики твердого тела

Движение твердого тела будет заданным, если имеется способ определения положения любой его точки в любой момент времени относительно некоторой системы отсчета. Для этого нет необходимости задавать движение каждой его точки, поскольку координаты точек твердого тела связаны соотношениями неизменности расстояний между ними. Для свободного твердого тела достаточно задать шесть независимых параметров. Покажем это.

Возьмем три точки тела, не лежащие на одной прямой. Девять декартовых координат этих точек связаны между собой соотношениями неизменности расстояния между точками:

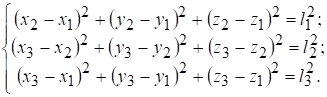
Поэтому положение трех точек тела определяется шестью независимыми координатами.

Если теперь добавить еще одну точку М, то ее положение определяется координатами, которые однако, связаны тремя условиями неизменности расстояний от точки М до точек :

Таким образом, число независимых параметров, определяющих положение четырех точек, остается шестью. Следовательно, оно останется шестью и для любого количества точек.

Число независимых параметров, задание которых определяет положение твердого тела в пространстве, называется числом степеней свободы тела.

Таким образом, свободное твердое тело имеет шесть степеней свободы. Если твердое тело закрепить в какой-либо точке, то оно уже будет иметь К=6 — 3 = 3 степени свободы.

Задать движение твердого тела не обязательно декартовыми координатами. В дальнейшем будет показано, что существует более удобные параметры, определяющие положение тела в пространстве.

Рассмотрим общую теорему кинематики, справедливую для любого движения твердого тела.

Теорема о проекциях скоростей двух точек тела

При любом движении твердого тела проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны.

Доказательство:

Возьмем произвольные точки тела А и В, скорость которых в некоторый момент времени обозначим и. Выберем произвольную неподвижную точку будут вектор-функциями и .

Из рис. 1.2.

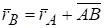
Продифференцируем по времени обе части равенства.

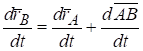
или.

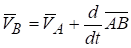
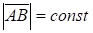
Так как при движении тела длина отрезка АВ не меняется, т. е., то из второго свойства производной вектора по скалярному аргументу.

.

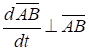
Проектируя теперь векторное равенство (6.4) на направление вектора, получим.

Простейшие движение твердого тела

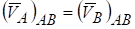
Существуют два простейших вида движения твердого тела, комбинированием которых можно получать другие, более сложные его движения. Такими движениями твердого тела являются поступательное движение и вращение вокруг неподвижной оси.

Поступательное движение твердого тела

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению.

Теорема:

Если твердое тело движется поступательно, то:

• 1. Траектории всех его точек одинаковы.
• 2. Скорости и ускорения всех точек тела в каждый момент времени равны между собой.

Доказательство:

Если выбрать две точки А и В твердого тела, то радиусы-векторы этих точек удовлетворяют условию При поступательном движении вектор является постоянным и по модулю и по направлению в любой момент времени.

Уравнения показывают, что годограф радиус-вектора точки В, являющийся траекторией этой точки, сдвинут по отношению к годографу радиус-вектора точки А (траектория точки А) на постоянный вектор. Если этот сдвиг осуществить, то обе траектории совпадают всеми своими точками. Такие траектории считаются одинаковыми. Следовательно, пункт 1) теоремы доказан. Далее продифференцируем по времени выражение:

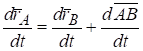
По первому свойству производной вектор-функции скалярного аргумента.

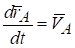
т.к. и поскольку и, то имеем.

Дифференцируя по времени (6.8) и учитывая, что.

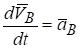
и ,.

получим Теорема доказана.

Поскольку все точки твердого тела при поступательном движении движутся одинаково, то поступательное движение полностью характеризуется движением одной точки тела. Для задания этого движения достаточно знать координаты какой-либо точки тела, как функции времени, т. е.

Следовательно, твердое тело, совершающее поступательное движение, имеет три степени свободы.

К = 3.

И уравнения (6.10) являются уравнениями поступательного движения твердого тела. Для изучения поступательного движения достаточно использовать кинематику точки.

Вращение твердого тела вокруг неподвижной оси

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором две точки тела остаются неподвижными в течение всего времени движения.

При этом остаются неподвижными все точки тела, расположенные на прямой, проходящей через неподвижные точки. Эта прямая называется осью вращения тела. Построим неподвижную плоскость, проходящую через ось вращения П₁, и подвижную плоскость П, скрепленную с вращающимся телом и также проходящую через ось вращения.

Пусть в начальный момент обе плоскости совпадают. Тогда в момент времени t положение подвижной плоскости и самого вращающегося тела можно определить двухгранным углом между плоскостями и соответствующим линейным углом между прямыми, расположенными в этих плоскостях и перпендикулярных оси вращения.

Этот угол называется углом поворота тела.

Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение.

= (t).

Зависимость выражает закон вращательного движения твердого тела вокруг неподвижной оси.

У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием одного параметра. К = 1.

Угол будем считать положительным, если он откладывается от неподвижной плоскости против хода часовой стрелки, и отрицательным — в противном случае, если смотреть с конца оси z. Дуговая стрелка на рис. 6.4 показывает направление положительного отсчета угла .

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.