Определение мест отгиба стержней в ребре балки

После подбора продольной арматуры в сечении 1−1 посередине пролета необходимо определить места отгибов арматурных стержней ребра по длине балки. Необходимость устройства отгибов связана с уменьшением изгибающих моментов при удалении от середины пролета, необходимостью закрепления в сжатой зоне бетона отгибаемых стержней и конструктивным наличием при отгибах наклонных участков стержней в ребре балки, воспринимающих растягивающие и скалывающие напряжения в ребре балки.

Конструктивно необходимо, чтобы 1/3 всего количества стержней растянутой арматуры было доведено до концов балки. Т. е. 12/3=4 стержня должны быть доведены до конца.

На рис. 5.3. изображена схема определения мест отгиба стержней в ребре балки для случая 12 стержней в ребре (рис. 5.2). Теоретические места отгиба стержней могут быть найдены графически или аналитически как места пересечения горизонтальных линий с эпюрой моментов. Указанные горизонтальные линии проведены с шагом Мпред/6, который определяет долю усилия, которое воспринимает каждая из групп (пар) стержней. В этом случае координаты теоретических обрывов стержней можно вычислить в виде:

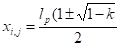
где — координаты (абсциссы) теоретических мест отгибов групп стержней (начало координат то есть х=0 в точке оси опирания на левой опоре),.

где i — номер группы стержней, для которых определяются места отгибов;

j — место отгиба группы стержней (j=1 — место отгиба у левой опоры, j=2 — место отгиба у правой опоры), причем.

.

.

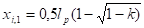
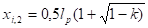
— расчетная длина балки,; - коэффициент, определяющий долю Мпред, воспринимаемую суммарно группами стержней, предшествующими отгибаемыми стержнями.

Поскольку эпюра моментов симметрична относительно середины пролета, то и теоретически места отгибов одной и той же группы стержней будут симметричны относительно середины пролета:

.

;

;

;

;

;

;

;

.

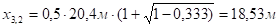
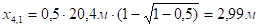
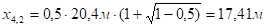
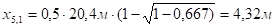
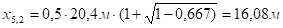
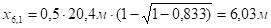
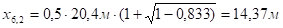
Фактические значения мест отгиба стержней определяют с учетом длин заводки (Дх) стержней за места теоретических отгибов:

;

.

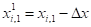
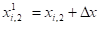
Длина заводки стержня за место теоретического отгиба для арматурной стали А-III должна составлять не менее 30d — при классе бетона В20 — В27,5, т. е. .

Для горизонтальных растянутых стержней необходима заводка их за оси опирания балки не менее 8d (1 и 2 пара стержней на рис. 5.3.). Кроме этого, крайние стержни, примыкающие к боковым поверхностям балки, должны быть отогнуты у торца под углом 90? и продолжены вверх до половины высоты балки (2 пара стержней на рис. 5.3.).

Остальные отгибаемые стержни должны иметь отгибы под углом б=30…45? к горизонту, причем любое вертикальное сечение в этой области должно пересекать хотя бы один наклонный стержень. Радиусы отгибов стержней R1 не менее 10d=0,28 м, а R2 не менее 3d=0,084 м (рис. 5). Горизонтальные прямолинейные участки стержней S в сжатой зоне ребра должны быть не менее 10d=0,28 м (от конца закругления).

;

;

;

;

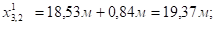
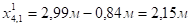
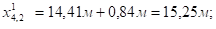
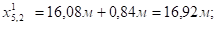
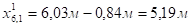
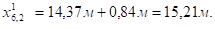
Рисунок 5.3. Схема положения мест отгибов стержней в ребре балки.