Выявление общей тенденции в рядах динамики

Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.

Различные результаты действия постоянных, периодических и разовых причин и факторов на уровни социально-экономических явлений во времени обусловливают необходимость изучения общей тенденции в рядах динамики.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Выявление основной тенденции развития называется в статистике также выравниванием временного ряда, а методы выявления тренда — методами выравнивания.

Выравнивание позволяет характеризовать особенности изменения во времени динамического ряда в наиболее общем виде как функцию времени, предполагая, что через время можно выразить влияние всех основных факторов. [16].

Методами выравнивания (статистического изучения тренда) являются: укрупнение периодов, сглаживание скользящей средней, аналитическое выравнивание.

Сглаживание путем укрупнения периодов заключается в определении итоговых или средних показателей для укрупненных интервалов времени. Укрупнение интервалов является одним из наиболее простых методов изучения основной тенденции в рядах динамики. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Сглаживание методом скользящей (подвижной) средней — определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, основная тенденция развития выражается в виде некоторой плавной линии. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т. д.), первых по счету уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т. д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. 9].

Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации. Например, сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям — на два члена в начале и конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике, выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.

Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. При этом методе исходные уровни ряда динамики заменяются теоретическими или расчетными, которые представляют собой некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др. [14].

Произведем выравнивание ряда динамики себестоимости зерна для более детального выявления тенденции.

Таблица 3 Выравнивание динамики урожайности подсолнечника в ЗАО «Николаевка» Аннинского района Воронежской области.

Метод укрупнения периодов и метод скользящей средней не выявили тенденции в изменении урожайности подсолнечника.

Выявим тенденцию изменения урожайности подсолнечника с помощью метода аналитического выравнивания.

Таблица 4 Аналитическое выравнивание урожайности подсолнечника в ЗАО «Николаевка» Аннинского района Воронежской области.

Для нахождения неизвестных параметров решается система нормальных уравнений:

подставим итоговые данные таблицы 4 в систему уравнений и рассчитаем значения коэффициентов уравнения.

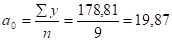
Параметр свидетельствует о том, что ежегодно в течение изучаемого периода урожайность подсолнечника увеличивалась на 2,18 ц/га.

Уравнение общей тенденции ряда динамики имеет вид:

Таким образом, получили выровненный ряд динамики урожайности подсолнечника, который говорит о ее систематическом повышении с годовым увеличением на 2,18 ц/га.

Полученные теоретические значения урожайности изобразим графически.

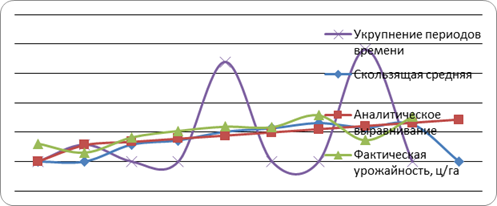
Кроме выравнивания по укрупнению периодов времени, скользящей средней и аналитического выравнивания, мы применим выравнивание по другим функциям.

Исходные данные получены на основе расчетов пакета прикладных программ StatGraf и отражены в приложении 2.

Таблица 5 Фактическая и выровненная урожайность подсолнечника в ЗАО «Николаевка» Аннинского района Воронежской области.

Анализируя данные таблицы, можно отметить, что ближе всего к фактическим показателям находятся выровненные значения урожайности по уравнению квадратической функции, относительно которых происходит ежегодное повышение урожайности подсолнечника.

Рассмотрим отклонение выровненных значений урожайности подсолнечника.

Таблица 6 Отклонение выровненных значений урожайности подсолнечника в ЗАО «Николаевка» Аннинского района Воронежской области.

По сравнению с другими функциями, в уравнении квадратической функции дисперсия и СКО незначительны, и равны соответственно 27,96 ц/га и 4,04 ц/га, а коэффициент вариации не превышает 33% и составляет 30,05%. Данные показатели подтверждают правильность выбора квадратичной функции как наиболее приближенной к фактическим значениям урожайности подсолнечника.

Графики данных функций отразим в приложении 3.

По уравнениям функций представим прогнозные значения урожайности.

Таблица 7 Прогнозные значения урожайности подсолнечника по уравнениям аналитического выравнивания в ЗАО «Николаевка» Аннинского района Воронежской области.

По данным таблицы видно, что в будущем в изучаемом предприятии по квадратической функции планируется постепенное снижении урожайности подсолнечника.

3 индексный анализ средней урожайности и валового сбора подсолнечника В статистике индексами называют относительные величины динамики, характеризующие изменение сложного явления во времени, в пространстве, элементы которого (т.е. явления) непосредственно не суммируются.

Индексы используются:

• 1) для характеристики общего изменения всех элементов сложного явления во времени, в пространстве и по сравнению с планом (нормой);
• 2) для оценки роли факторов в изменении сложных явлений;
• 3) для анализа влияния структурных сдвигов в экономике.

Индексы различают по ряду признаков. [1].

В зависимости от объектов исследования индексы могут быть объемных и качественных показателей:

Объемные показатели характеризуют объем, численность совокупности, численность работающих, объем продукции в натуральных измерителях и др.

К качественным показателям относятся: цена, себестоимость, трудоемкость, производительность труда, урожайность и др.

В зависимости от охвата элементов изучаемой совокупности индексы различают: индивидуальные, групповые и общие.

Индивидуальные индексы характеризуют изменение отдельного явления или элемента совокупности. Рассчитываются индивидуальные индексы отношением уровня явления отчетного (текущего) периода к уровню базисного периода. Индивидуальный индекс — это условное название, потому, что он связан с общими и групповыми индексами. Это относительная величина динамики (коэффициент) и назначение его — расширение возможностей общих и групповых индексов.

Общие (сводные) индексы — это относительные показатели, характеризующие изменение сложного явления, состоящего из элементов неподдающихся непосредственно суммированию.

Групповые индексы — это относительные величины, характеризующие изменение явления по группе. В зависимости от базы сравнения индексы различают: базисные — база постоянная и цепные — база переменная. В зависимости от методологии расчета существуют агрегатная форма и средний: индекс арифметический и гармонический. 9] Проведем индексный анализ средней себестоимости и производственных затрат на зерно на примере предприятий Аннинского и Павловского районов Воронежской области. Исходная информация представлена в таблице 8. Определим общие изменения средней урожайности подсолнечника:

относительное изменение покажет общий индекс средней урожайности:

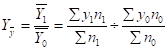
Данный индекс называется индексом переменного состава, т.к. в нем изменяются оба элемента, а именно посевная площадь и урожайность подсолнечника.

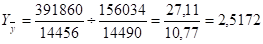
или.

абсолютное изменение составит:

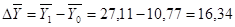
ц/га.

Следовательно, средняя урожайность подсолнечника в отчетном периоде по сравнению с базисным повысилась на 151,72% или 16,34ц.

Средняя урожайность подсолнечника находится под влиянием двух факторов:

Изменение урожайности в отдельных предприятиях.

Изменение структуры посевных площадей.

Таблица 8 Индексный анализ средней урожайности и валового сбора подсолнечника.

Наименование предприятий.	Посевная площадь. га.	Урожайность, ц/га.	Валовой сбор подсолнечника, ц.	Структура посевной площади, %.
факт.	усл.
АННИНСКИЙ Р-Н ЗАО «Николаевка».			3,73.	30,38.				4,48.	2,08.
ООО «АГТ Верхне Тойденский».			7,59.	25,8.		15 918,6.		4,28.	4,27.
ООО «Нива».			10,21.	27,23.		9557,73.		3,00.	2,43.
ООО «Комсомольское».			9,85.	26,12.				1,59.	1,73.
ООО Агротех-гарант «Пугачевский».			7,13.	25,67.		14 426,54.		4,35.	3,89.
ЗАО «Дружба».				30,4.				6,21.	5,53.
ЗАО «Путь Ленина».			17,92.	33,11.				3,42.	3,46.
СХА «Заря».			13,6.	36,1.		8844,5.		1,38.	1,69.
СПК «Агро-Нива».			6,42.					1,29.	1,38.
СПК «Русь».								0,62.	0,48.
ООО «Агротех-Гарант Нащекино».			9,81.	25,99.		12 891,04.		3,60.	3,43.
ООО «Агротех-Гарант Рубашевский».			8,18.	24,9.				3,22.	1,94.
ООО «Агротех-Гарант Хлебородное».			10,43.	24,19.		29 511,8.		4,25.	8,44.
ПАВЛОВСКИЙ Р-Н ООО «Нива».			2,9.	10,84.				5,52.	4,15.
ООО «Красный Дон».			7,71.	28,57.		10 770,89.		2,41.	2,61.
ООО «Воронцовское».			13,16.	44,54.		27 570,26.		3,59.	4,28.
ООО «Агрофирма Тихий Дон».			7,51.	25,89.		15 896,46.		3,97.	4,25.
ЗАО «Славяне».			6,3.	27,9.