Определение напряженного состояния плоско пространственных систем

Определение напряженного состояния плоско пространственных систем

Для заданной плоскопространственной рамы требуется: 1) раскрыть статическую неопределимость, 2) построить эпюры изгибающих и крутящих моментов, 3) определить коэффициент запаса по текучести, используя гипотезу энергии формоизменения. Для расчета принять: F = 1 kн; l = 0,4 м;

G=0,4E.

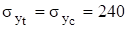
МПа; мм,.

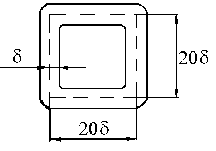
Cечение представляет собой тонкостенный замкнутый профиль.

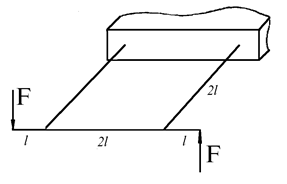
Плоскопространственными называются системы, плоские в геометрическом отношении, но нагруженные силовыми факторами, перпендикулярными к плоскости рамы.

Особенностью этих систем является то, что внутренние силовые факторы во всех поперечных сечениях рамы, лежащие в плоскости рамы равны нулю.

Заданная плоскопространственная рама шесть раз статически неопределима.

Для решения задачи разрежем раму по оси косой симметрии. В месте разреза возникает шесть внутренних силовых факторов:

Х₁— поперечная сила, лежащая в вертикальной плоскости Х₂— поперечная сила, действующая в горизонтальной плоскости (лежит в плоскости рамы).

Х₃— крутящий момент Х₄— продольная сила (лежит в плоскости рамы).

Х₅— изгибающий момент, действующий в горизонтальной плоскости (лежит в плоскости рамы).

Х₆— изгибающий момент, действующий в вертикальной плоскости.

Чтобы не затенять рисунок, факторы х_4; x₅ и х₆, действующие на левую половину рамы, вынести на отдельную схему.

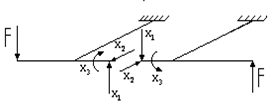
В соответствии с особенностями плоскопространственной рамы X₂=0;

X₄=0; X₅=0.

Следовательно, расчетная схема приобретает вид:

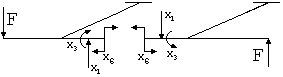
Для полученной расчетной схемы записываем систему канонических уравнений и строим эпюры изгибающих и крутящих моментов от действия внешних нагрузок и усилий: X ₁=1; X₃=1 и X₆=1.

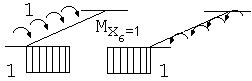
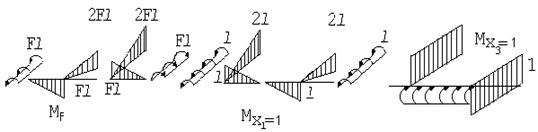
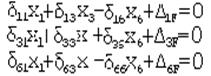
Определяем коэффициенты, входящие в систему уравнений. Для их определения необходимо знать моменты инерции заданного сечения при изгибе и кручении.

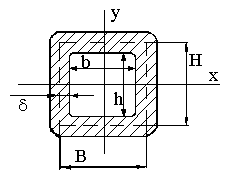
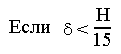
Момент инерции при изгибе определяется как :

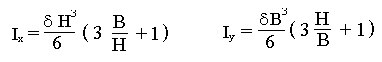
В остальных случаях :

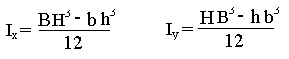
В нашем случае: H=21; B=21.

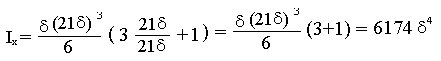
Момент инерции при кручении определяется как.

I_t=4A_o²/S ,.

Где А_о=(B-)(H-) — площадь сечения по серединному контуру.

S=2[(B-)+(H-)] - длина периметра серединного контура.

В нашем случае :

_o=(20)²=400²; S=4*20=80.

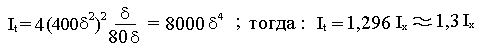
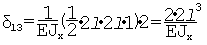
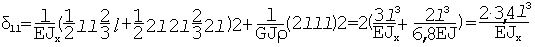
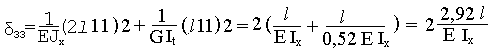
₁₆=₆₁=0 ₃₆=₆₃=0.

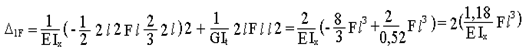
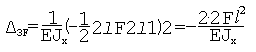
_6F=0.

Из последнего уравнения системы получаем, что х₆ — изгибающий момент, являющийся симметричным фактором, при кососимметричном нагружении рамы оказался равным 0.

Таким образом, для плоскопространственных рам, как и для плоских рам справедливо свойство симметрии и косой симметрии.

Решаем систему, состоящую из двух первых уравнений, сократив все коэффициенты на общий множитель (2/(EI_x)).

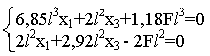
Получаем, что х₁= - 0,46 °F.

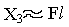
Строим эпюры изгибающих моментов от истинных значений х₁ и х₃.

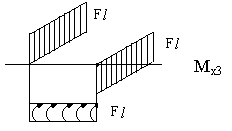
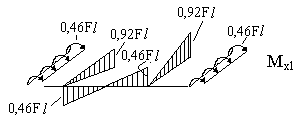
Строим суммарные эпюры изгибающих и крутящих моментов.

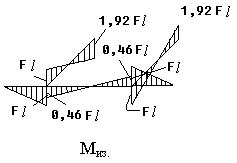
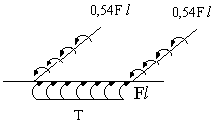
Наиболее опасными будут сечения в заделке.

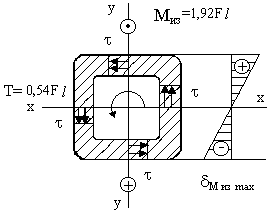
Рассмотрим сечение в левой заделке. Т.к. эпюры изгибающих моментов строятся на сжатых волокнах, то низ сечения будет испытывать нормальные напряжения сжатия, а верх — растяжения (см. эпюру).

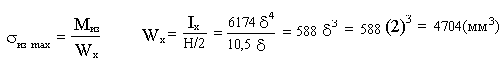
М_из=1,92Fl=1,92*1*10³*0,4*10³=0,768*10⁶(Hмм).

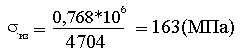
Касательные напряжения по толщине стенки постоянны и одинаковы во всех точках сечения.

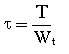
W_t=2A_o=2*400²*=800³=800(2)³=6400 (мм³).

T=0,54Fl=0,54*1*10³*0,4*10³=0,216*10⁶ (н *мм).

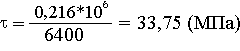
Определяем эквивалентные напряжения.

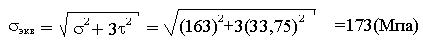
Определим коэффициент запаса по текучести.

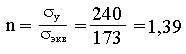
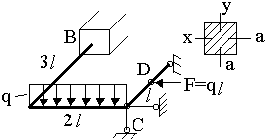
Плоскопространственная рама, изготовлена из прутка квадратного поперечного сечения (а=20 мм), нагружена так, как показано на рисунке. Определить допускаемую нагрузку, если материал — сталь СТ 3 (у_adm=160Мпа) и характерный размер конструкции l=0,2 м.

Для определения допускаемой нагрузки необходимо проанализировать напряженное состояние материала конструкции в наиболее нагруженном сечении. Построение эпюр внутренних силовых факторов невозможно без раскрытия статической неопределимости.

Заданная рама три раза статически неопределима. (В заделке В возникает 6 реакций связей; на опоре С — две реакции; на опоре Д — одна) уравнений статики в пространстве — 6).

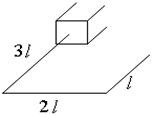
Отбрасывая «лишние» связи, получаем следующую основную систему.

Превращаем основную систему в систему, эквивалентную заданной и записываем систему канонических уравнений метода сил.

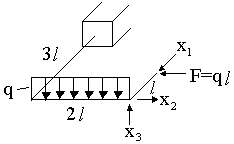
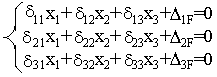
Для определения коэффициентов, входящих в эту систему, строим эпюры изгибающих моментов от внешних нагрузок и сил х₁; x₂; х₃; равны 1.

При построении грузовой эпюры используем метод независимости действия сил.

грузовая эпюра сечение напряженное состояние.

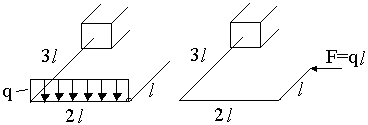
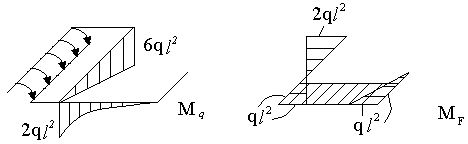
Эпюры изгибающих моментов от единичных нагрузок имеют вид:

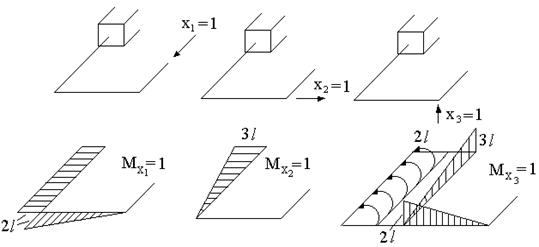
Определяем коэффициенты системы канонических уравнений.

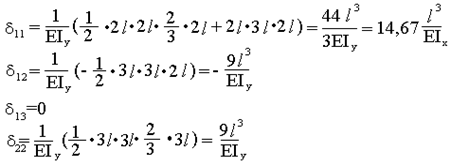
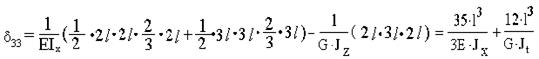
Для квадратного сечения:

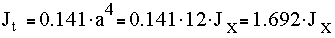
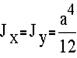
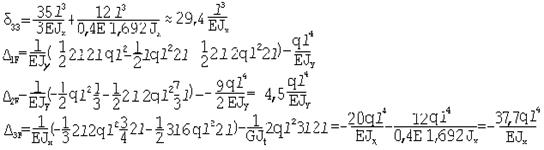
Подставляем найденные значения в систему канонических уравнений и сокращаем на общий множитель Ejx.

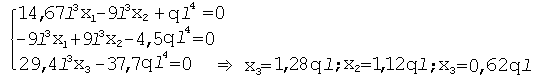
Перестраиваем эпюры от единичных нагрузок с учетом найденных значений усилий x.

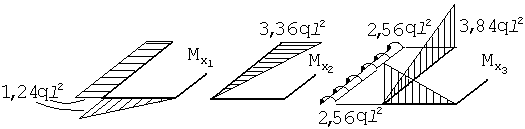
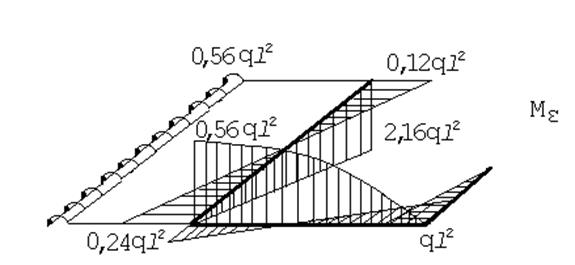
И строим суммарную эпюру изгибающих моментов.

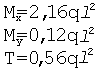
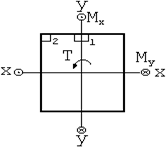
Наиболее опасным является сечение в заделке.

Наиболее опасными будут точки 1 и 2, в которых возникают наибольшие напряжения.

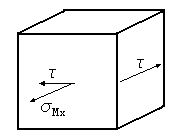
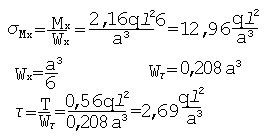
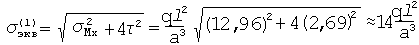
Точка 1: Так как гипотеза, по которой необходимо определить эквивалентные напряжения, не оговорена, принимаем гипотезу наибольших касательных напряжений.

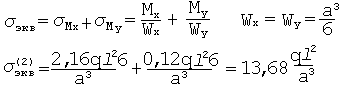
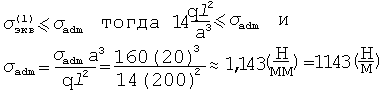
Точка 1 более опасна, поэтому для определения допускаемой нагрузки используем. Условия прочности.

Анализируем характер напряженного состояния в различных точках сечения.

Все точки, лежащие в верхней части сечения, находятся в одинаковом напряженном состоянии. Для примера рассмотрим точку l, лежащую на оси y. Определим главные напряжения в этой точке.

Все точки, лежащие в нижней части сечения, тоже находятся в одинаковом напряженном состоянии. Поэтому для анализа выбираем точку 2, тоже лежащую на оси у. Определяем главные напряжения в этой точке.

Феодосьев В. И. Сопротивление материалов.- М: Наука, 2006. 512 с.

Писаренко Г. С., Яковлев А. Н., Матвеев В. В. Справочник по сопротивлению материалов.- Киев: Наук. думка, 2005. 704 с.