Практическая часть. 
Процесс принятия управленческих решений

Задача № 1.

Фирма занимается поставками леса. Длина маршрута 650 км. Себестоимость 1 м³ леса — 180 грн., а цена реализации — 260 грн. за 1 м³. В зависимости от вместительности транспортных средств фирма может осуществлять поставки партиями по 15, 20, 25, 30, 35 м³ леса. Цена реализации может скакать в зависимости от того, на сколько дней опаздывает поставка:

• — без опозданий — 260 грн/м3;
• — на 1 день опаздывает — 250 грн/м3;
• — на 2 дня опаздывает — 240 грн/м3;
• — на 3 дня опаздывает — 230 грн/м3;
• — на 4 дня опаздывает — 220 грн/м.

Фирма оплачивает доставка на место прибытие в зависимости от объема груза:

• — 15 м³ = 450 грн;
• — 20,25, 30 м³ = 550 грн;
• — 35 м³ = 800 грн.

Кроме того, фирма тратит 80 грн за каждый просроченный день.

На основании статистических данных анализа предыдущих ситуаций фирма может оценить вероятность прибытия товара в срок таким образом:

• — Р1 (без опозданий) = 0,3;
• — Р2 (на день опаздывает) = 0,3;
• — Р3 (на 2 опаздывает) = 0,2;
• — Р4 (на 3 дня опаздывает) = 0,1;
• — Р5 (на 4 дня опаздывает) = 0,1.

Фирма получила заявку на поставку. В условиях вышесказанной неопределенности найдите оптимальную стратегию для фирмы (используя теорию игор).

РЕШЕНИЕ:

Без опозданий.

• 15* (260−180) — 450= 750
• 20*(260−180) — 550 = 1050
• 25*(260−180) — 550 = 1450
• 30*(260−180) — 550 = 1850
• 35*(260−180) — 800 = 2000

На 1 день опаздывает:

• 15* (250−180) — 450−80*1= 520
• 20*(250−180) — 550 — 80*1= 770
• 25*(250−180) — 550 — 80*1= 1120
• 30*(250−180) — 550 — 80*1= 1470
• 35*(250−180) — 800 -80*1= 1570

На 2 дня опаздывает:

• 15* (240−180) — 450−80*2= 290
• 20*(240−180) — 550 — 80*2= 490
• 25*(240−180) — 550 — 80*2= 790
• 30*(240−180) — 550 — 80*2= 1090
• 35*(240−180) — 800 -80*2= 1140

На 3 дня опаздывает:

• 15* (230−180) — 450−80*3= 60
• 20*(230−180) — 550 — 80*3= 210
• 25*(230−180) — 550 — 80*3= 460
• 30*(230−180) — 550 — 80*3= 710
• 35*(230−180) — 800 -80*3=710

На 4 дня опаздывает:

• 15* (220−180) — 450−80*4= -170
• 20*(220−180) — 550 — 80*4= -70
• 25*(220−180) — 550 — 80*4= 130
• 30*(220−180) — 550 — 80*4= 330
• 35*(220−180) — 800 -80*4= 280

Составим платежную матрицу.

Проведем анализ платежной матрицы и исключим невыгодные стратегии.

Вследствии чего, матрица будет иметь следующий вид:

Составим матрицу рисков:

Оценим стратегию с помощью критериев:

Критерий Байеса — Лапласа Задача № 2.

ОАО «Интерпродукт» решает заключить договор на поставку продуктов питания с одной из трех баз. Собрав все данные о сроках оплаты товара этими базами (таблица), необходимо выбрать базу, которая оплачивает за товар в наименьшие сроки при заключении договора поставки продукции (по коэффициенту вариации).

Решение:

Номер события.	Сроки оплаты в днях x.	Число случаев наблюдения п.
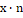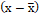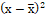1-я база.
				— 5,61.	31,47.	944,10.
				— 1,61.	2,59.	72,58.
				— 0,61.	0,37.	8,19.
				2,39.	5,71.	228,40.
				4,39.	19,27.	578,10.
		1831,37.
2-я база.
				— 6,61.	43,69.	1267,07.
				— 2,61.	6,81.	143,05.
				— 1,61.	2,59.	93,16.
				0,39.	0,15.	7,5.
				2,39.	5,71.	177,07.
				6,39.	40,83.	1347,46.
		3035,31.
3-я база.
				— 8,58.	73,62.	3091,89.
				— 6,58.	43,30.	1472,20.
				— 0,58.	0,34.	10,76.
				0,42.	0,18.	4,94.
				2,42.	5,86.	199,12.
				5,42.	29,38.	851,92.
				6,42.	41,22.	1071,63.
				7,42.	55,06.	1376,41.
		8078,87.

Для первой базы, исходя из формул:

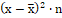
Для второй базы.

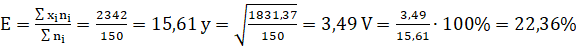
Для третьей базы.

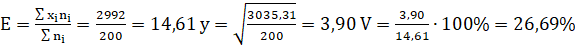
Коэффициент вариации для первой базы наименьший, что говорит о целесообразности заключить договор поставки продукции с этой базой.

Рассмотренные примеры показывают, что риск имеет математически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана с достаточно высокой степенью точности. При выборе наиболее приемлемого решения было использовано правило оптимальной вероятности результата, которое состоит в том, что из возможных решений выбирается то, при котором вероятность результата является приемлемой для предпринимателя. На практике применение правила оптимальной вероятности результата обычно сочетается с правилом оптимальной колеблемости результата. Как известно, колеблемость показателей выражается их дисперсией, средним квадратическим отклонением и коэффициентом вариации. Сущность правила оптимальной колеблемости результата заключается в том, что из возможных решений выбирается то, при котором вероятности выигрыша и проигрыша для одного и того же рискового вложения капитала имеют небольшой разрыв, т. е. наименьшую величину дисперсии, среднего квадратического отклонения вариации. В рассматриваемых задачах выбор оптимальных решений был сделан с использованием этих двух правил.

Задача № 3.

Финансовому менеджеру необходимо выбрать привлекательный проект. В проект, А необходимо вложить: 1 год — 25 млн. грн.; 2 год — 35 млн. грн; (всего 60 млн. грн); в проект Б: 1 год — 55 млн. грн; 2 год — 10 млн. грн (всего 65 млн. грн). Норма рентабельности (норма прибыльности) — q = 10%.

Потоки ожидания прибыли от проектов составляют:

• А) проект А: 1 год — 27 млн. грн; 2 год — 20 млн. грн; 3 год — 12 млн. грн; 4 год — 9 Млн. грн; 5 год — 7 млн. грн.
• Б) проект Б: 1 год — 40 млн. грн; 2 год — 35 млн. грн; 3 год — 10 млн. грн; 4 год -5 млн. грн.

Решение:

Проект «А».

IC = 60 млн. грн.

Ожидаемые денежные потоки:

P1 = 27 млн. грн.

P2 = 20 млн. грн.

P3 = 12 млн. грн.

P4 = 9 млн. грн.

P5 = 7 млн. грн.

Q = 10%.

Проект «В».

IC = 65 млн. грн.

Ожидаемые денежные потоки:

P1 = 40 млн. грн.

P2 = 35 млн. грн.

P3 = 10 млн. грн.

P4 = 5 млн. грн.

Q = 10%.

Определим чистый приведенный доход по каждому проекту:

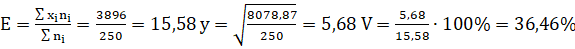
(3.1).

где:

NPV — чистый приведенный доход, тыс. $,.

CF — будущий денежный поток, тыс.$,.

IC — инвестиции, тыс.$.

I — ставка дисконта в виде коэффициента.

NPVА = 27/(1+0.1) + 20/(1+0.1)2 + 12/(1+0.1)3+9/(1+0.1)4+7/(1+0.1)5−60.

= 0,635 млн. грн.

NPVВ = 40/(1+0,1) + 35/ (1+0,1) 2 + 10/(1+0.1)3+5/(1+0.1)4 — 65.

= 76,23−65 = 11,23 млн. грн Рассчитаем индекс рентабельности:

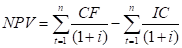
(3.2.).

PI А= 60,635/60 = 1,01.

PI В= (11,23 + 65) / 65 = 1,17.

Период окупаемости.

PPА = ((60−27−20−12)/9)*12.

PP А= 3 года и 1 месяц.

PP В= ((65−40)/35) * 12.

PP В= 1 год 8,5 месяцев ВЫВОД: Для реализации выбираем инвестиционный проект «Б».

Он рентабельный, окупается, что увеличивает стоимость компании.

управленческий решение достижение.