Выбор места размещения диаграммы

В появившемся диалоговом окне «Мастер диаграмм (шаг 4 из 4): размещение диаграммы» выбираем переключатель «Поместить диаграмму на имеющемся листе» (рис. 9). Диаграмма будет внедрена в текущем рабочем листе. Если выбрать переключатель «Поместить диаграмму на листе отдельном», то соответственно, график появится на отдельном листе.

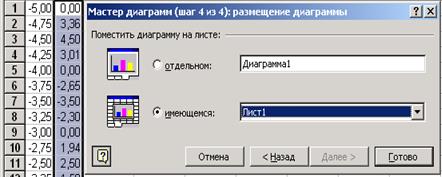
Рис. 9. Диалоговое окно «Мастер диаграмм (шаг 4 из 4): размещение диаграммы»

Итак, график построен (рис. 10). Теперь, используя маркеры изменения размеров, можно поменять ее размер, а так же разместить диаграмму в нужном месте рабочего листа.

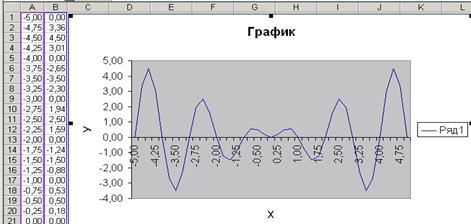
Рис. 10. Построенный график данной функции из примера

Кроме того, допустимо редактирование и исправление внешнего облика любого элемента диаграммы. Для этого достаточно его выделить, нажать на правую кнопку мыши и из появившегося контекстного меню выбрать команду редактирования этого элемента.

Пример 2. Средствами Excel постройте график функции с двумя условиями:

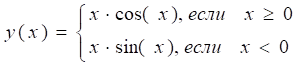
при x[-5;5], Дx = 0,25.

Решение.

График строится по алгоритму, представленному в примере 1. Отличие состоит в том, что в ячейку В1 вводится формула:

= ЕСЛИ (А1?0; А1*COS (A1);A1*SIN (A1)).

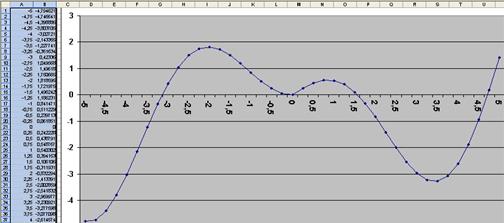
Рис. 11. График функции заданной с двумя разветвлениями

Пример 3. Средствами Excel постройте график функции с тремя условиями:

при x[-5;5], Дx = 0,25.

Решение.

График строится по алгоритму, представленному в примере 1, за иск-лючением того, что в ячейку В1 вводится формула:

= ЕСЛИ (А1= -1; А1<=1); A1³; A1*SIN (A1)^2)).

или.

= ЕСЛИ (А1< -1; А1*COS (A1)^2; ЕСЛИ (А1<=1; A1³; A1*SIN (A1)^2)).

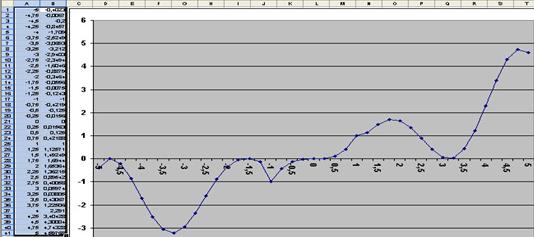
Рис. 12. График функции заданной с тремя разветвлениями

Пример 4. Средствами Excel постройте в одной системе координат графики функций.

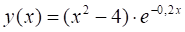
и.

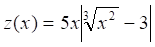
при x [-5;5], Дx = 0,25.

Решение.

Алгоритм построение графиков данных функций состоит из следующих шагов:

В ячейку А1, В1 и С1 введем соответственно x, y и z.

В диапазоне ячеек А2: А42 введем значения аргумента x от -5 до 5 с шагом 0.25.

В ячейки В2 и С2 введем формулы:

= (A2²−4)*exp (-0.2*A2).

=5*A2*ABS ((A2²)^(1/3)-3).

Выделим диапазон В2: С2, установив указатель мыши на маркер заполнения этого диапазона и прибуксируем его вниз до тех пор, пока не получится числовой ряд нужной длины, т. е. пока не заполняется числовыми данными диапазон В3: С42.

Выбираем команду «Вставка» затем «Диаграмма» .

В появившемся диалоговом окне «Мастер диаграмм (шаг 1 из 4): тип диаграммы» на вкладке «Стандартные» в списке «Тип» выбираем «График», а в списке «Вид» укажем стандартный график и нажимаем кнопку «Далее» .

В появившемся окне «Исходные данные» на вкладке «Диапазон данных» выбираем переключатель «Ряды в столбцах», В поле ввода «Диапазон» приведем ссылку на диапазон данных В2: С42, значения из которого откладываются вдоль оси ординат.

На вкладке «Ряд» диалогового окна «Исходные данные» в поле ввода «Подписи оси Х» укажем ссылку на диапазон А2: А42, значения из которого откладывается по оси абсцисс (рис. 13). В списке «Ряд» приводим ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных).

Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода «Диапазон» предыдущего шага алгоритма. В поле «Значения» автоматически вводится ссылка на диапазон, соответствующий выбранному ряду из списка «Ряд». В поле ввода «Имя» отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда.

Выбираем в списке «Ряд» элемент «Ряд 1». В поле ввода «Имя» укажем ссылку на ячейку В1 (идентификатор данного ряда). Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле «Имя» автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, = Лист 1!$В$ 1. Теперь осталось только щелкнуть на элементе «Ряд1» списка «Ряд». Это приведет к тому, что элемент «Ряд1» поменяется на «у», т. е. на то значение, которое содержится в ячейке В1. Аналогично поступаем с элементом «Ряд 2» списка «Ряд». Сначала выбираем его, затем в поле ввода «Имя» укажем ссылку на ячейку С1, а потом щелкнем на элементе «Ряд2» (рис. 14). Нажимаем кнопку «Далее» .

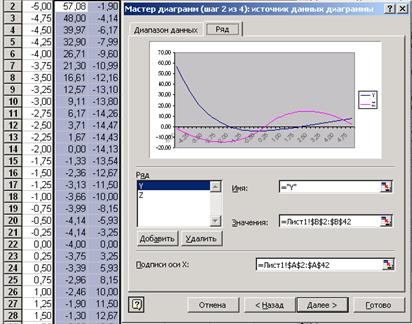
Рис. 14. Вкладка «Ряд» диалогового окна «Исходные данные» после задания имен рядов

В появившемся диалоговом окне «Мастер диаграмм (шаг 3 из 4): параметры диаграммы» на вкладке «Заголовки» в поле «Название диаграммы» введем «График двух функций», в поле «Ось Х (категорий)» введем «х», в поле «Ось Y (значений)» введем «y», «z». На вкладке «Легенда» установим флажок «Добавить легенду», Нажмем кнопку «Далее» .

В появившемся диалоговом окне «Мастер диаграмм (шаг 4 из 4): размещение диаграммы» выбираем переключатель «Поместить диаграмму на листе имеющемся». «Диаграмма (график)» будет внедрена в текущий рабочий лист. Если выбираем переключатель «Поместить диаграмму на листе отдельном», то диаграмма будет помещена на новом рабочем листе. Для получения графика нажимаем клавишу «Готово» .

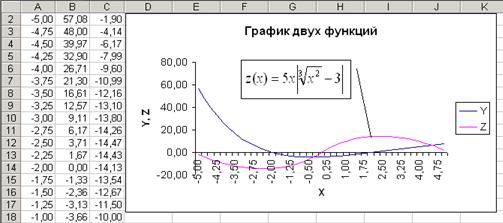
Рис. 15. Графики функций y (x) и z (x), построенные в одной системе координат

После построения графика данных функций можно провести некоторое редактирование. Например, для того, чтобы пользователю было легче отличить, какая линия является графиком функции «у» а какая — «z», можно изменить вид графика «у» или «z». С этой целью выделим график функции «z». Нажимаем правую кнопку мыши и в появившемся контекстном меню выбираем команду «Формат рядов данных». На вкладке «Вид» диалогового окна «Формат ряда данных», используя элементы управления групп «Маркер» и «Линия», установим необходимые линии графика. Нажимаем кнопку «ОК» .

Можно изменить фон графика. Для этого выделим диаграмму (график) (но не область построения). Нажимаем правую кнопку мыши и в появившемся контекстном меню выбираем команду «Формат области диаграммы» .

На вкладке «Вид» диалогового окна «Формат области диаграммы» установим флажок «скругленные углы», а используя элементы управления группы «Заливка» установим цвет и вид заливки фона. Нажимаем кнопку «ОК» .

Пример 5. Средствами Excel постройте график (поверхность) следующей функции, зависящей от двух аргументов:

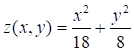
при x[-2;2], y[-2;2], Дx = 0,2, Дy = 0,2.

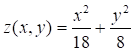
Решение. Алгоритм построения поверхности заданной формулой состоит из следующих этапов:

Введем значения переменной «х» в столбец А. Для этого в ячейку А2 вводится первое значение аргумента, т. е. -2. В ячейку А3 — второе значение аргумента, т. е. -1.8. Затем, выделив блок ячеек А2: А3 автозаполнением получаем все значения аргумента «х» в диапазоне А2: А22.

Значения переменной «y» вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной, т. е. — 2, а в ячейку С1 второе значение, т. е. -1.8. Затем, выделив блок ячеек В1: С1, автозаполнением получаем все значения аргумента «y» в диапазоне В1: W1.

Вводим значения переменной z. Для этого в ячейку В2 вводим формулу =$A2²/18+B$ 1²/8, после чего нажимаем клавишу «Enter». Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу в диапазон В2: W2, после чего (протягиванием вниз) в диапазоне B2: W22. В результате в диапазоне В22: W22 появится таблица точек эллиптического параболоида (рис. 16).

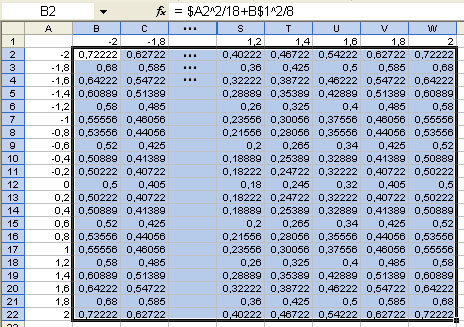
Рис. 16. Таблица значений функции, зависящей от двух аргументов

Построим поверхность по результатам табуляции. для этого на панели инструментов «Стандартная» выберем кнопку «Мастер диаграмм». В появившемся диалоговом окне «Мастер диаграмм (шаг 1 из 4): тип диаграммы» указываем тип диаграммы — «Поверхность» и вид — «Проволочная» (прозрачная) поверхность. Нажимаем кнопку «Далее» .

В появившемся диалоговом окне «Мастер диаграмм (шаг 2 из 4): источник данных диаграммы» необходимо выбрать вкладку «Диапазон данных» и в поле «Диапазон» мышью указать интервал данных В2: W22. Нажимаем кнопку «Далее» .

Выбираем вкладку «Ряд», а поле «Подписи оси Х», указываем диапазон подписей. Для этого следует активизировать данное поле, щелкнув в нем указателем мышью и ввести диапазон подписей оси «х» — А2: А22.

Вводим значения подписей оси y. Для этого в рабочем поле «Ряд» выбираем первую запись «Ряд1» и, активизировав рабочее поле «Имя», указателем мыши вводим первое значение переменной «у» -2. Затем в поле «Ряд» выбираем вторую запись «Ряд2» и в рабочее поле «Имя» вводим второе значение переменной «у» — 1,8 и т. д. После появления требуемых записей следует нажать кнопку «Далее» .

В появившемся диалоговом окне необходимо ввести заголовок диаграммы и названия осей. Для этого нужно выбрать вкладку «Заголовки», щелкнув по ней указателем мыши. После чего в рабочем поле «Название диаграммы» ввести с клавиатуры название «Эллиптический параболоид». Затем аналогичным образом вводим в рабочее поле «Ось Х» (категорий), «Ось Y» (рядов данных) и «Ось Z» (значений) соответствующие названия «х», «y» и «z». На вкладке «Легенда» сбросим флажок «Добавить легенду» и нажмем кнопку «Готово». В результате получим искомую поверхность (рис. 17).

Рис. 17. Эллиптический параболоид