Каустики в пространстве

Все становиться на порядок сложнее и намного интересней, если рассматривать каустики в трехмерном пространстве. В трехмерном пространстве есть две точки скопления энергии. По-другому можно сказать, что поверхность каустики в пространстве состоит из пары листов.

Для примера возьмем отражающую поверхность следующего вида:

.

И направим на не сверху пучок параллельно оси z. Если рассматривать плоскость y = 0, то мы получим отражение от параболы z = x², а в плоскости x = 0 отражение будет идти от параболы z = 2y². Получаться разные параболы, и лучи от них будут скапливаться на разных высотах и в разных точках по оси z. Одна из точек будет находиться на одном листе нашей каустической поверхности, а вторая на другом.

Рисунок 1.3 -За счет перепада давления стекла прогибаются внутрь В последнее время в Интернете находят фотографии ярких четырехугольных звезд на стенах сооружений. Эти рисунки являются результатом отражения лучей солнца от пластиковых окон близ лежащих домов.

Это обусловлено тем, что в окнах из пластика между стеклами герметизируется, и воздух между ними выкачивается. Из-за перепада давления каждое из стекол деформируется внутрь и напоминает форму, продемонстрированную на рисунке 1.3 (изображение достаточно сильно растянуто вдоль вертикальной оси). Поверхность, изображенную на рисунке можно хорошо приблизить графиком следующей функции:

.

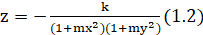
подобрав соответствующие константы k и m.

Если ограничить кусок окна некоторой поверхностью и направить лучами света, направленными сверху параллельным пучком, а на пути света поставить экран, то при незначительном удалении от нашего окна мы сможем наблюдать на экране картинку, основным фрагментом этой картинки будет являться звезда, состоящая из восьми углов (рис. 1.4 (a)). Если же экран будет отодвинут на большее расстояние, то мы сможем увидеть звезду, состоящую из четырех углов, на фоне наиболее меньшего овала (рис. 1.4(б)), что будет соответствовать реальным фотографиям. Четыре отсутствующих по сравнению с левым рисунком луча оказались отрезанными от звезды из-за того, что мы рассматриваем отражение только от ограниченного куска поверхности — от квадратного окна.

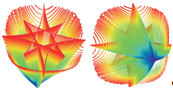
Рисунок 1.5- Два вида на каустическую поверхность Теперь попробуем изобразить саму каустическую поверхность, подобную заданному каустическому изображению. Она фактически будет собрана из двух листов. На рисунке 1.5 цветом зафиксировано удаление точек каустики от заданной поверхности: синие точки находятся ближе к поверхности, красные — дальше от поверхности. Сечением одного из листов нашей каустики будет звезда из восьми углов, сечение другого будет границей окружающего звезду овала.

Каустики могут образовываться не только при отражении, но и при преломлении света, скажем на поверхности воды.

Смоделируем это явление, задав преломляющую поверхность уравнением:

.

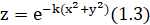
Рисунок 1.7- Каустическая поверхность, образующаяся при преломлении на воздушном пузырьке, А вот и соответствующая каустическая поверхность для преломленных лучей (рис. 1.7). Синие точки расположены ближе к поверхности воды, а красные более удалены от нее. Сечение внутренней поверхности представляет собой четырехугольную звезду, а внешней — граница овала, содержащего эту звезду.

Табл. 1. Кривые и их каустики.