Математическая модель прогнозирования экологического состояния малых водных объектов на примере прудов Волгоградской агломерации

В статье рассмотрена модель математического определения параметров экологического состояния поверхностных водных объектов на примере прудов Волгоградской агломерации на основании статистических данных по основным загрязнителям природных вод с возможностью составления длительного прогноза развития.

Ключевые слова: экологическое состояние, малые водные объекты, пруды, загрязнители, качество воды, математическая модель, водный баланс.

Волгоградская агломерация имеет население более миллиона человек, которое постоянно увеличивается, другой особенностью является его протяженность, составляющая более 100 км, это приводит к увеличению темпов антропогенного влияния на поверхностные водные объекты. Соответственно очень быстро изменяются балансы и процессы переноса веществ, как в пределах локальных областей, так и в более широком масштабе [1, 2].

Многолетние исследования качества воды прудов Волгоградской агломерации позволили комплексно исследовать статистическую базу с целью прогнозирования развития экологической ситуации на водных объектах.

Существует ряд общеизвестных математических зависимостей, характеризующих протекание природных процессов [3]. Однако их трудно применить к реальным условиям, поскольку представленные данные пригодны для идеальных процессов в лабораторных условиях [4], без привязки его к конкретному объекту и его экологическим циклам [5, 6].

Анализ статистических данных с 2008 по 2013 г. позволил выявить математические зависимости между содержанием хлоридов и сульфатов, БПК (биологическое потребление кислорода), ХПК (химическое потребление кислорода) и сухим остатком в пробах воды, железа и суммарного содержания металлов в воде, донных отложениях и почве, нефтепродуктами в воде и почве [7]. При проверке полученных математических зависимостей была установлена высокая степень достоверности.

На основании полученных математических зависимостей была разработана общая математическая модель, которая позволяет сократить перечень контролируемых показателей и в дальнейшем производить их пересчет с использованием коэффициентов, сокращая материальные, финансовые и временные затраты на обследование малых водных объектов [8, 9]. Алгоритм пересчета величин представлен на рис. 1.

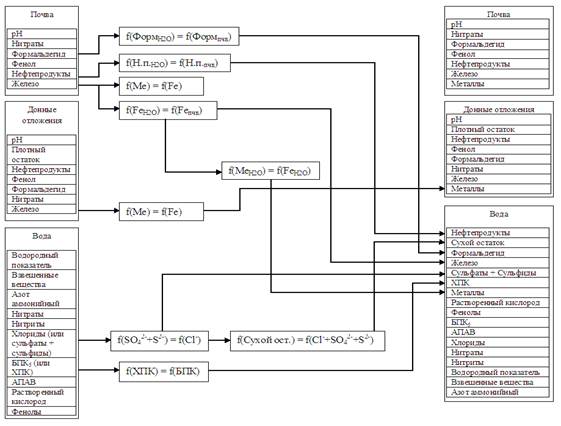
Рис. 1. — Алгоритм математической модели

Блоки модели выбраны на основе взаимосвязанных групп показателей: ХПК и БПК; сухого остатка, хлоридов, сульфатов и сульфидов; железа и группы металлов; нефтепродуктов и формальдегида в зависимости от содержания в почве, воде и донных отложениях за сезон [10]. Таким образом, в состав модели входят 4 блока. Пятый блок модели позволяет спрогнозировать величины показателей с учетом 4-х летней цикличности процессов. Цикличность развития экологической обстановки прудов Волгоградской агломерации характеризуется наличием двух видов циклов — для группы северных и южных прудов. Различие между группами заключается в тенденции изменения контролируемых показателей качества, отражающихся на коэффициентах. Общее уравнение для составления прогноза имеет вид: экологический волгоградский математический.

.

где К — коэффициент пропорциональности, Д — погрешность полученных результатов.

Значение коэффициентов пропорциональности при составлении экологического прогноза для прудов Волгоградской агломерации приведены в таблице.

Таблица 1 Коэффициенты пропорциональности уравнений для прогноза.

Используя полученные математические зависимости содержания одних веществ относительно других и уравнения для составления прогноза можно составить прогноз на любой срок для широкого перечня контролируемых параметров.

Объединенная математическая модель для расчета и прогнозирования концентраций веществ в прудах Волгоградской агломерации может быть использована не только для удешевления программ контроля экологической обстановки на региональных водных объектах, но и разработки долгосрочных мероприятий по реабилитации экосистем водоемов. Разработанная методика составления математической модели перспективна для составления экологического прогноза состояния малых водных объектов в других регионах.

• 1. Черемных М. Э., Попова О. В., Забалуева А. И. Анализ причин загрязнения вод Таганрогского залива нефтепродуктами // Инженерный вестник Дона. 2014. № 2. URL: ivdon.ru/ru/magazine/archive/n2y2014/2391.
• 2. Frid C. Ecology of Aquatic Management. London: Pearson Education Limited, 2012. 274 p.
• 3. Шитиков В. К., Тихонов В. Н., Быков С. Т., Ковалев А. Ф. Статистический анализ и нормальность распределения выборок в токсиколого-гигиенических исследованиях // Гигиена и санитария. 1985. № 3. С. 61−62.
• 4. Алимов А. Ф. Элементы теории функционирования экосистем. СПб.: ЗИН РАН, 2000. 147 с.
• 5. Лапач С. Н., Чуйсенко А. В., Бабич П. И. Статистические методы в медико-биологических исследованиях с использованием Excel. М.: Мориос.
• 6. Bishop C. Neural Networks for Pattern Recognition. Oxford: University Press, 2005. 432 р.
• 7. Талыбов М. А., Сафаров Д. Т., Черунова И. В., Сирота Е. Н., Колесник С. А. Экспериментальные исследования для развития информационной базы минеральных вод // Инженерный вестник Дона. 2014. № 3. URL: ivdon.ru/ru/magazine/archive/n3y2014/2536
• 8. Васильев В. И., Ильясов Б. Г. Интеллектуальные системы управления с использованием генетических алгоритмов. Уфа: УГАТУ, 1999. 105 с.
• 9. Виттих В. А. Системообразующая функция интеграции знаний в организациях // Препринт Самара. 1998. № 2. С. 20.
• 10. Балушкина Е. В. Структура сообществ донных животных и оценка экологического состояния р. Ижоры: оценка качества вод р. Ижоры по структурным характеристикам донных животных в разные годы // Биология внутренних вод. 2002. № 4. С. 61−68.