Пространственный аспект учебного процесса

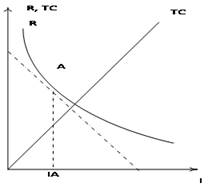
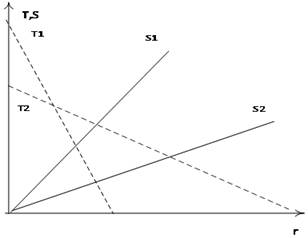
Графически, стационарное состояние производителя, определяется как точка касания прямой, перпендикулярной прямой транспортных издержек и кривой ренты. На рисунке 1 представлена графическая интерпретация модели Тьюнена.

Рисунок 1. — Графическое решение модели Тьюнена:

Возрастающее значение образования, на фоне ускорения информационных процессов, детерминируют поиск условий эффективности учебного процесса. Объем знаний человечества удваивается каждые 5 лет, а время обучения специалистов сохраняется на прежнем уровне. Традиционно, методология образования абстрагируется от пространственных аспектов обучения, изучая главным образом, организационно-технические аспекты учебного процесса. В работе представлена точка зрения, с позиции которой, значительный потенциал совершенствования образования кроется в плоскости пространственной организации учебного процесса. Идея написания статьи возникла во время анализа модели Тьюнена.

Анализ модели, осмысление механизмов, обуславливающих эволюцию структуры размещения производительных сил, привели к мысли, что они могут быть использованы для объяснения структуры аудитории. Действительно, является выбор места в аудитории случайным, и если нет, то каковы механизмы образования структуры аудитории, влияет структура аудитории на поведение преподавателя, каковы условия организации эффективного учебного процесса?

Эти вопросы и составили предмет исследования. Соавторами статьи, можно по праву считать студентов группы 13 МО 01 Академии ИМСИТ, чьи критические замечания существенно способствовали пониманию проблемы.

Цель работы: исследовать пространственный аспект учебного процесса, сформулировать необходимые условия эффективного обучения.

Цель определила необходимость решения следующих задач:

• 1. Сформулировать понятия для формального описания проблемы;
• 2. Определить границы, переменные проблемы, сформулировать связи, решающие правила, процедуры;
• 3. Создать модель учебного процесса;
• 4. Провести анализ модели;
• 5. Определить условия эффективного учебного процесса.

Классическим примером исследования пространственного аспекта целенаправленной деятельности человека является модель Тьюнена. В различных модификациях она составила научный базис те:

На расстоянии lA, предельные рентные платежи уравновешивают предельные транспортные издержки. В чем отличие рисунка 1 от классических кругов Тьюнена. Концепция колец помогает установить, где могут оказаться производители, в то время как рисунок 1 определяет, где окажется производитель.

Какое отношение модель Тьюнена имеет к исследуемой проблеме? Как посмотреть. Формализуем проблему. Действующие лица: преподаватель, студенты. Цель занятия: владение знаниями, навыками.

Функции: преподаватель передает информацию, устанавливает обратную связь, определяет уровень усвоения материала, ставит оценки.

Студент получает, обрабатывает информацию, демонстрирует понимание информации. Способность к обработке информации примем пропорциональной достигнутому уровню.

Иными словами между темпом знания и достигнутым уровнем существует положительная обратная связь. Чем больше знает студент, тем больший объем материала он освоит за урок. На рисунке 2 представлена структура обратной связи.

Рисунок 2. — Положительная обратная связь между уровнем и скоростью знаний:

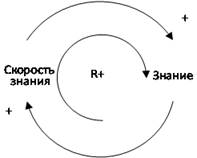
Положения модели:

Функция, назовем ее функцией нагрузки, возвращает количество информации, которое передает преподаватель на расстояние r. Преподаватель может выбрать различные функции: постоянная нагрузка, убывающая нагрузка:

Если на лекции он использует постоянную нагрузку (передает студентам один объем информации), то на семинаре, он может выбрать убывающую нагрузку.

Это выражается в том, что преподаватель задает больше вопросов тем, кто рядом с ним, чаще проверяет решение задач. Такой характер взаимодействия не случаен.

На семинаре требуется оценить степень освоения материала, а значит необходимо слышать, видеть студентов. Чем дальше студент, тем меньше желания у преподавателя это делать:

Функция, назовем ее функцией студента, возвращает количество информации, которое обрабатывает студент на расстояние r:

Количество информации, которое может обработать за урок студент, В качестве можно рассматривать текущую оценку студента. Максимальный объем информации, студент может получить возле преподавателя. Параметр n характеризует чувствительность студента к шуму. Шум пропорционален расстоянию от преподавателя.

Плохое зрение, слух, отвлечение других студентов — примеры шума. Вот и все, что нам потребуется для анализа.

А теперь в аудиторию! Предположим в аудитории преподаватель и студент. Преподаватель транслирует с постоянной нагрузкой. Студент знает нагрузку преподавателя. Если он на занятии первый раз, то узнав уровень нагрузки, может поменять место.

На рисунке 3 представлены возможные результаты занятия. Случай T = S0 является наиболее подходящим.

Преподаватель транслирует с интенсивностью равной максимальной производительности студента, и студент оказывается возле него.

Если T < S0, студент скучает и пересаживается подальше.

Рисунок 3. — Структура аудитории при постоянной нагрузке преподавателя на 1 студента (разработано автором):

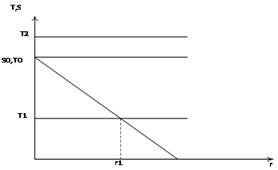
И наконец, если T > S0, студент покидает аудиторию, на любом расстоянии от преподавателя интенсивность информации недоступна. Представим, что мы зашли в аудиторию и увидели студента сидящего рядом с преподавателем. Это равносильно тому, что T = S0.

Если студент отдалился от преподавателя, значит, уровень нагрузки, ниже потенциального уровня студента, канал информации недостаточно нагружен, что равносильно потерям. И наконец, если преподаватель один в аудитории, выбранный уровень нагрузки выше потенциала студента, канал перегружен. Предположим в аудитории преподаватель и четыре студента, текущие оценки которых 5, 4, 3, 2. Это равносильно тому что, что равносильно максимальной явке. На рисунке 4 представлена структура аудитории, при нагрузке не выше возможностей самого слабого студента. Не правда ли, необычная расстановка? Отличники сидят позади остальных. Объем переданной за урок информации равен, потеря информации в такой структуре равна. Возникает вопрос, какую нагрузку следует установить, чтобы максимизировать объем переданной за урок информации?

Рисунок 4. — Структура аудитории при максимальной явке (разработано автором):

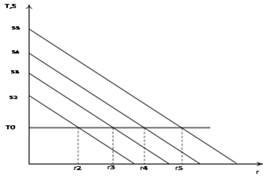
Пусть функция R (результат), возвращает объем информации, переданный за занятие в зависимости от нагрузки. Тогда:

R (2) = 8;

R (3) = 12;

R (4) = 8;

R (5) = 5.

Таким образом, оптимальной является нагрузка, ориентированная на троечника. Если изменить структуру группы, например, увеличив долю отличников, то изменится и оптимальная нагрузка.

Пусть состав группы. Тогда:

R (2) = 16;

R (3) = 21;

R (4) = 24;

R (5) = 25.

Очевидно, оптимальный выбор — ориентация на отличников. Сформулируем правило установления нагрузки:

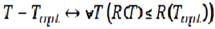
Если перейти к набору, то необходимо перейти на уровень хорошиста. Скептик справедливо заметит: в большинстве аудиторий отличники сидят впереди остальных. Наша простенькая модель может объяснить и это! Итак, мы установили, что если в аудитории два студента различной степени подготовленности, и одинаковой устойчивостью к шуму, более подготовленный студент сидит позади другого. Увеличим чувствительность «отличника». Рисунок 5 демонстрирует распределение студентов в аудитории при различной чувствительности к шуму.

Рисунок 5. — Структура аудитории при максимальной явке (разработано автором):

Хорошист оказывается впереди троечника. Знакомая картина. Прелесть в том, что теперь известна причина этого.

В заключение, рассмотрим пример псевдозанятия. Его правила следующие: Преподаватель ориентируется на достигнутый уровень. Если студент отвечает на все поставленные ему вопросы, он получает оценку текущего уровня. Иными словами, студент в любом месте аудитории получает один результат. Его задача донести его до преподавателя с минимальными потерями. Когда преподаватель выбирает такую модель.

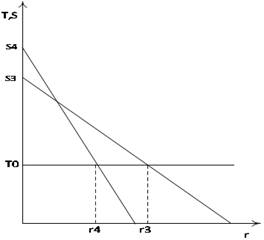
Если он недостаточно подготовлен для организации эффективного контроля знаний. Его цель — провести время со студентами в аудитории. Эта задача аналогична модели Тьюнена. Рента — количество вопросов, шум — транспортные издержки. На рисунке 6 распределение студентов в аудитории. Ограничимся двумя студентами и линейной функцией нагрузки. Пунктирной линий обозначена нагрузка преподавателя, равносильно количество вопросов. Сплошной линией обозначена потеря информации.

Рисунок 6. — Распределение студентов в условиях неэффективного контроля знаний (разработано автором):

образование гносеологический преподаватель Проведем анализ рисунка. Если преподаватель установит нагрузку Т1, то оба студента окажутся на последней парте. Если нагрузка составит Т2, то оба студента окажутся на первой парте. Как рассадить студентов — дифференцировать нагрузку.

Рисунок 7. — Упорядоченное распределение студентов в аудитории (разработано автором):

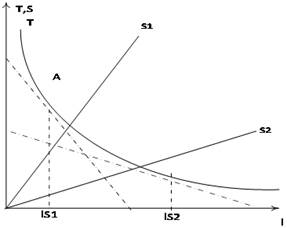
Таким образом, продемонстрировано, что регулируя нагрузку, преподаватель может «управлять» распределением студентов в аудитории.

Исследование проведено в соответствии с заявленной целью. В рамках принятых допущений, установлены причины (достаточные условия) формирования определенных структур аудитории.

Доказано, что преподаватель может управлять структурой, задавая пространственное распределение учебной нагрузки. Теоретическое значение работы заключается в том, что она расширяет знания о механизмах, процессах передачи, обработки информации, групповой динамики, формирования структур и управления ими. Методологическое значение проявляется в возможности совершенствования учебного процесса. Автор будет благодарен коллегам за критические замечания.

• 1. Thunen, von J.H. (1826), Der Isolierte Staat in Beziehung auf Landschaft und Nationalokonomie. Trans. By C.M. Wartenberg (1966) Von Thunen’s Isolated State. Oxford: Pergamon Press.
• 2. Alonso, W. (1964). Location and land use. Cambridge: Harvard university press.
• 3. Thunen, von J.H. (1826), Der Isolierte Staat in Beziehung auf Landschaft und Nationalokonomie. Trans. By C.M. Wartenberg (1966) Von Thunen’s Isolated State. Oxford: Pergamon Press.
• 4. Alonso, W. (1964). Location and land use. Cambridge: Harvard university press.