Основная часть. 
Результаты экспериментальных исследований обмолачивающего устройства с эластичными гребенками

В результате проведения поисковых и отсеивающих экспериментов были определены наиболее значимые факторы и их интервалы варьирования. Интервалы и уровни варьирования факторов приведены в таблице.

Таблица. Уровни и интервалы варьирования факторов

Для того чтобы определить оптимальное сочетание выделенных факторов, были проведены эксперименты согласно матрице планирования полного факторного эксперимента 2³, которая включала восемь опытов. После проведения экспериментов проводилось крутое восхождение по поверхности отклика [5]. лен обмолот гребень барабан По их результатам были определены коэффициенты регрессии: b₀ = 93,025; b₁ = 1,517; b₃ = 1,667; b₆ = 3,133; b_1,3 = 0,458; b_1,6 = 0,375; b_3,6 = 0,708, и статическая оценка полученной линейной модели: t _b0 = 348,844; t _b1 = 5,687; t _b3 = 6,25; t _b6 = 11,75; t _b1,3 = 1,719; t _b1,6 = 1,406; t _b3,6 = 2,656.

Проверку адекватности представления результатов экспериментов полиномом первой степени осуществляли путем сравнения табличного критерия Фишера с расчетным. Расчетное значение критерия Фишера F_р=5,698 больше табличного, поэтому гипотеза об описании результатов экспериментов линейной моделью отвергается.

На основании проведенных расчетов можно сделать заключение, что линейная модель.

(1).

для описания результатов эксперимента не может быть принята. Поэтому в дальнейших исследованиях с целью изучения и описания области оптимума линейного приближения недостаточно, т. е. необходимо использовать планирование второго порядка, позволяющее получить представление о функции отклика с помощью полинома второй степени.

Несмотря на то что линейная модель для рассматриваемой зависимости оказалась неадекватной, мы провели крутое восхождение по поверхности отклика с помощью полученных коэффициентов регрессии в кодированном виде, предполагая, что при удачном движении можно установить более благоприятные условия для проведения следующей стадии эксперимента.

После крутого восхождения, когда линейного приближения поверхности отклика становится недостаточно, проводят описание почти стационарной области уравнениями второго порядка, которые учитывают кривизну поверхности отклика. В сельском хозяйстве для большинства технологических процессов с допустимой погрешностью 5% обычно достаточным является описание поверхности отклика полиномом второго порядка [5].

Для описания области оптимума уравнениями второго порядка в условиях неоднородностей Боксом и Бенкиным разработаны трехуровневые планы. Их отличительной особенностью является то, что во всех строках плана некоторые факторы находятся на нулевых уровнях. По сравнению с ортогональными и рототабельными, трехуровневые планы Бокса и Бенкина более экономичны и к тому же обладают свойствами вышеназванных планов [5].

В результате анализа нами был выбран трехуровневый план второго порядка Бокса-Бенкина для трех факторов, включающий 15 опытов. Опыты проводились в трехкратной повторности в рандомизированном порядке. С учетом данных крутого восхождения центр эксперимента был выбран в новой точке.

По вышеприведенной методике для критерия Е была получена следующая адекватная модель:

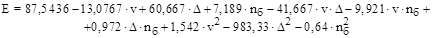
(2).

где v — скорость подачи ленты, м/с; Д — зазор между гребнем и подбарабаньем, м; n_б — частота вращения барабана, с^-1.

В результате ее решения были получены рациональные параметры исследуемых факторов: v=1,41 м/с; Д=0,01 м; n_б=5,67 с^-1. После их подстановки в уравнение (3) получили значение степени обмолота Е=99,4%. В результате экспериментов, проведенных при этих же уровнях факторов, значение степени обмолота составило 98,43%. Разность между расчетным и экспериментальным значениями не превышает 5%. На основании этого можно сделать вывод, что экспериментальные данные хорошо согласуются с расчетными и подтверждаются ими.