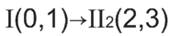Структурный и кинематический анализ механизма

1. Структурный анализ механизма

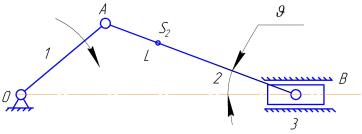
Рисунок 1 — План механизма.

Определяем степень подвижности механизма.

В нашем случае механизм плоский (траектории всех точек звеньев перемещаются параллельно плоскости). Поэтому степень подвижности находим по формуле Чебышева:

W_п. = 3n — 2P₅ — P₄,.

где W_п. — число степеней свободы для плоского механизма;

n=3 — число подвижных звеньев;

P₅=4 — число пар 5-го класса;

P₄=0 — число пар 4-го класса;

W_п. = 3•3 — 2•4 — 0 = 1,.

Определяем число избыточных связей Число избыточных связей q в действительном механизме равно:

W_пр. = 6n — 5P₅ — 4P₄ — 3P₃ — 2P₂ — P₁,.

W_пр. = 6•3 — 5•4 = - 2.

q = 1 — (-2) = 3.

где W_пр. — число степеней свободы для пространственного механизма Определяем вид кинематических пар механизма:

• (0−1) — вращательная, низшая, V класса
• (1−2) — вращательная, низшая, V класса
• (2−3) — вращательная, низшая, V класса
• (0−3) — поступательная, низшая, V класса

Разделяем механизм на группы Ассура:

I (0,1) — начальный механизм.

II₂ (2,3) — группа Ассура II класса 2-го вида 2-го порядка.

Составим формулу строения механизма:

Исследуемый механизм является механизмом II класса.

2. Кинематический анализ механизма

механизм структурный кинематический анализ Таблица 1. Исходные данные.